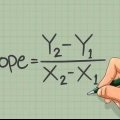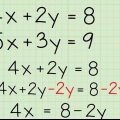Voorbeeld: ons weet dit  en
en  , en dus
, en dus  .
. 
Voorbeeld:
foon  aan elke kant:
aan elke kant: 
Trek 3 van elke kant af: 
Deel elke kant deur 3:  .
.
Voorbeeld: en
en 



Voorbeeld: en
en 



Dit is dieselfde antwoord as wat voorheen verkry is. Ons het geen foute gemaak nie. 
Voorbeeld: en
en 
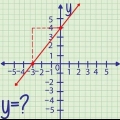
Die twee lyne sny by die punt (3.6). 
As die twee lyne parallel is, sal hulle nie sny nie . Die x-terme kan uitgeskakel word en jou vergelyking kan vereenvoudig word na `n ongeldige vergelyking (soos bv  ). Let hier`die lyne sny nie of nie `n geldige oplossing nie` as jy antwoord.
). Let hier`die lyne sny nie of nie `n geldige oplossing nie` as jy antwoord. As die twee vergelykings dieselfde lyn beskryf, dan `sny` hulle mekaar oral. Jy kan die x-terme uitskakel en jou vergelyking tot `n geldige vergelyking vereenvoudig (soos  ). skryf neer `die twee lyne is dieselfde` as antwoord.
). skryf neer `die twee lyne is dieselfde` as antwoord. 

Voorbeeld: Vind die kruising van  en
en  .
. Herskryf die kwadratiese vergelyking in terme van y:  en
en  .
.Hierdie voorbeeld het een kwadratiese vergelyking en een lineêre vergelyking. Probleme met twee kwadratiese vergelykings word op dieselfde manier opgelos. 
Voorbeeld: en
en 


Voorbeeld:
Trek x van elke kant af: 
Trek 7 van elke kant af: 

Voorbeeld:
Die doel van faktorisering is om die twee faktore te bepaal wat saam vermenigvuldig word om hierdie vergelyking te produseer. Vanaf die eerste kwartaal weet ons dit  kan in x en x verdeel word. Skryf (x )(x ) = 0 om dit te wys.
kan in x en x verdeel word. Skryf (x )(x ) = 0 om dit te wys. Die laaste kwartaal is -6. Skryf elke paar faktore neer wat vermenigvuldig het om -6 te gee as die produk:  ,
,  ,
,  , en
, en  .
. Die middelterm is x (wat jy as 1x kan skryf). Tel elke paar faktore bymekaar om 1 as `n antwoord te kry. Die regte paar faktore is  , want
, want  .
. Vul die gapings in jou antwoord in met hierdie paar faktore:  .
. 
Voorbeeld (faktor): Ons eindig met die vergelyking  . As beide faktore tussen hakies gelyk is aan 0, dan is die vergelyking waar. Die een oplossing is
. As beide faktore tussen hakies gelyk is aan 0, dan is die vergelyking waar. Die een oplossing is  →
→  . Die ander oplossing is
. Die ander oplossing is  →
→  .
. Voorbeeld (kwadratiese vergelyking of deelvierkant): As jy een van hierdie metodes gebruik om die vergelyking op te los, sal `n vierkantswortel verskyn. Byvoorbeeld, ons vergelyking word  . Onthou dat jy `n vierkantswortel tot twee verskillende oplossings kan vereenvoudig:
. Onthou dat jy `n vierkantswortel tot twee verskillende oplossings kan vereenvoudig:  , en
, en . Skryf twee vergelykings, een vir elke moontlikheid, en los vir x vir elk van hulle op.
. Skryf twee vergelykings, een vir elke moontlikheid, en los vir x vir elk van hulle op. 
Een oplossing: Die probleme kan in twee identiese faktore verdeel word ((x-1)(x-1) = 0). Ingevoer in die kwadratiese formule, word die vierkantswortel  . Jy hoef net een vergelyking op te los.
. Jy hoef net een vergelyking op te los. Daar is geen werklike oplossing nie: Daar is geen faktore wat aan die vereistes voldoen nie (notering tot die middeltermyn). Ingevoer in die kwadratiese formule kry jy `n negatiewe getal onder die radikaal (soos  ). Skryf `geen oplossing` as jou antwoord.
). Skryf `geen oplossing` as jou antwoord. 
Voorbeeld: Ons het twee oplossings gevind,  en
en  . Een van ons lyne het die vergelyking
. Een van ons lyne het die vergelyking  . plaasvervanger
. plaasvervanger  en
en  , en los elke vergelyking op sodat jy kry
, en los elke vergelyking op sodat jy kry  en
en  as jy `n antwoord kry.
as jy `n antwoord kry. 
Voorbeeld: Wanneer ons  insette, kry ons
insette, kry ons  , sodat een snypunt gelyk is aan (2, 9). Ons doen dieselfde vir die tweede oplossing, en dit gee ons die snypunt (-3, 4) aan.
, sodat een snypunt gelyk is aan (2, 9). Ons doen dieselfde vir die tweede oplossing, en dit gee ons die snypunt (-3, 4) aan.
Bereken die snypunt van twee lyne
Inhoud
Wanneer reguitlyne op `n tweedimensionele grafiek sny, doen hulle dit by slegs een punt, aangedui deur die koördinate x en y. Aangesien beide lyne deur daardie punt gaan, weet jy dat die x- en y-koördinate aan beide vergelykings moet voldoen. Met `n paar ekstra tegnieke kan jy die snypunte van parabole en ander kwadratiese krommes vind, met dieselfde logika.
Trappe
Metode 1 van 2: Bepaling van die kruising tussen twee reguitlyne

1. Skryf die vergelyking van enige lyn met y aan die linkerkant. Indien nodig, verander die vergelyking sodat y aan die een kant van die gelykheidsteken geïsoleer is. As die vergelyking met f(x) of g(x) in plaas van y geskryf word, skei daardie term. Onthou dat jy terme kan uitskakel deur dieselfde bewerking aan beide kante uit te voer.
- Is die vergelykings onbekend, bepaal dit dan gebaseer op die inligting wat gegee is.
- Voorbeeld: Gestel jy het twee lyne
en
. Om y in die tweede vergelyking te skei, tel 12 by elke kant:

2. Maak seker dat die regtersye van die vergelykings gelyk is. Ons soek `n punt waar die twee lyne dieselfde x- en y-waardes het; dit is die punt waar die lyne sny. Beide vergelykings het slegs `n y aan die linkerkant, so ons weet dat die regtersye gelyk aan mekaar is. Skryf `n nuwe vergelyking wat dit wys.
 en
en  , en dus
, en dus  .
.
3. Los x in die vergelyking op. Die nuwe vergelyking het net een veranderlike, x. Los dit op met algebra deur dieselfde bewerking aan beide kante uit te voer. Vind die x-terme van elke kant van die vergelyking en plaas dit in die vorm x = __ (indien nie moontlik nie, lees verder aan die einde van hierdie afdeling).

 aan elke kant:
aan elke kant:

 .
.
4. Gebruik hierdie x-waarde om vir y op te los. Kies die vergelyking van elke lyn. Vervang elke x in die vergelyking met die antwoord wat jy gevind het. Los nou op vir y.
 en
en 



5. Gaan jou werk na. Dit is wys om jou x-waarde in die ander vergelyking in te prop om te sien of jy dieselfde resultaat kry. As jy `n ander oplossing vir y kry, gaan terug en kontroleer jou werk vir foute.
 en
en 




6. Skryf die x- en y-koördinate van die kruising neer. Jy het nou die x-waarde en y-waarde van die snypunt van die twee lyne opgelos. Skryf die punt as `n koördinaat, met die x-waarde as die eerste getal.
 en
en 

7. Verwerk ongewone resultate. Sommige vergelykings maak dit onmoontlik om x op te los. Dit beteken nie noodwendig dat jy `n fout gemaak het nie. Daar is twee maniere waarop `n paar lyne tot `n spesiale oplossing kan lei:
 ). Let hier`die lyne sny nie of nie `n geldige oplossing nie` as jy antwoord.
). Let hier`die lyne sny nie of nie `n geldige oplossing nie` as jy antwoord. ). skryf neer `die twee lyne is dieselfde` as antwoord.
). skryf neer `die twee lyne is dieselfde` as antwoord.Metode 2 van 2: Probleme met kwadratiese vergelykings

1. Leer om kwadratiese vergelykings te herken. In `n kwadratiese vergelyking is daar een of meer veranderlikes in kwadratiese vorm ( of
of  ), en daar is geen hoër magte nie. Die lyne wat deur vergelykings voorgestel word, is geboë, en kan dus `n reguit lyn in 0, 1 of 2 punte sny. In hierdie deel sal jy leer hoe om die kruisings van so `n probleem te vind.
), en daar is geen hoër magte nie. Die lyne wat deur vergelykings voorgestel word, is geboë, en kan dus `n reguit lyn in 0, 1 of 2 punte sny. In hierdie deel sal jy leer hoe om die kruisings van so `n probleem te vind.
 of
of  ), en daar is geen hoër magte nie. Die lyne wat deur vergelykings voorgestel word, is geboë, en kan dus `n reguit lyn in 0, 1 of 2 punte sny. In hierdie deel sal jy leer hoe om die kruisings van so `n probleem te vind.
), en daar is geen hoër magte nie. Die lyne wat deur vergelykings voorgestel word, is geboë, en kan dus `n reguit lyn in 0, 1 of 2 punte sny. In hierdie deel sal jy leer hoe om die kruisings van so `n probleem te vind. - Werk vergelykings tussen hakies uit om te sien of hulle kwadraties is. Byvoorbeeld,
is kwadraties, want jy kan dit buite hakies plaas as
- Met vergelykings van `n sirkel of `n ellips albei a
soos `n
termyn. As jy hierdie spesiale gevalle moeilik vind, lees verder by Wenke aan die einde van hierdie artikel.

2. Skryf die vergelykings in terme van y. Indien nodig, herskryf elke vergelyking sodat y aan die een kant is.
 en
en  .
. en
en  .
.
3. Kombineer die twee vergelykings om die y uit te skakel. As jy albei vergelykings gelyk aan y gemaak het, dan weet jy dat die twee vergelykings sonder die y gelyk is aan mekaar.
 en
en 


4. Herrangskik die nuwe vergelyking sodat een kant gelyk is aan nul. Gebruik standaard wiskundige metodes om alle terme aan die een kant van die vergelyking te kry. Dit is die vereiste opstelling van die probleme om dit in die volgende stap te kan oplos.




5.Los die kwadratiese vergelyking op. As jy een sy gelyk aan nul het, is daar drie maniere om die kwadratiese vergelyking op te los. Almal verkies `n ander metode. Jy kan meer lees oor die kwadratiese formule van `verdeel die vierkant`, of jy kan hierdie voorbeeld verder volg daarvoor faktoriseer metode:

 kan in x en x verdeel word. Skryf (x )(x ) = 0 om dit te wys.
kan in x en x verdeel word. Skryf (x )(x ) = 0 om dit te wys. ,
,  ,
,  , en
, en  .
. , want
, want  .
. .
.
6. Hou jou oë oop vir twee oplossings vir x. As jy te vinnig werk, sal jy dalk een antwoord vir die probleem vind sonder om te besef dat daar `n ander is. Hier is hoe om die twee x-waardes te vind vir lyne wat by twee punte sny:
 . As beide faktore tussen hakies gelyk is aan 0, dan is die vergelyking waar. Die een oplossing is
. As beide faktore tussen hakies gelyk is aan 0, dan is die vergelyking waar. Die een oplossing is  →
→  . Die ander oplossing is
. Die ander oplossing is  →
→  .
. . Onthou dat jy `n vierkantswortel tot twee verskillende oplossings kan vereenvoudig:
. Onthou dat jy `n vierkantswortel tot twee verskillende oplossings kan vereenvoudig:  , en
, en . Skryf twee vergelykings, een vir elke moontlikheid, en los vir x vir elk van hulle op.
. Skryf twee vergelykings, een vir elke moontlikheid, en los vir x vir elk van hulle op.
7. Los probleme op met een of geen oplossings. Twee lyne wat skaars aan mekaar raak, het een kruising, en twee lyne wat nooit aan mekaar raak nie, het nul. U kan hulle op die volgende maniere herken:
 . Jy hoef net een vergelyking op te los.
. Jy hoef net een vergelyking op te los. ). Skryf `geen oplossing` as jou antwoord.
). Skryf `geen oplossing` as jou antwoord.
8. Prop die x-waardes terug in die oorspronklike vergelyking. Sodra jy die x-waarde van die kruising het, plaas dit terug in een van die vergelykings waarmee jy begin het. Los vir y op om die y-waarde te vind. As daar `n tweede x-waarde is, herhaal ook vir hierdie waarde.
 en
en  . Een van ons lyne het die vergelyking
. Een van ons lyne het die vergelyking  . plaasvervanger
. plaasvervanger  en
en  , en los elke vergelyking op sodat jy kry
, en los elke vergelyking op sodat jy kry  en
en  as jy `n antwoord kry.
as jy `n antwoord kry.
9. Skryf die antwoord as koördinate. Nou skryf jy die antwoord as koördinate, met die x-waarde en y-waarde van die kruising. As jy twee antwoorde het, maak seker dat jy die korrekte x-waarde met elke y-waarde pas.
 insette, kry ons
insette, kry ons  , sodat een snypunt gelyk is aan (2, 9). Ons doen dieselfde vir die tweede oplossing, en dit gee ons die snypunt (-3, 4) aan.
, sodat een snypunt gelyk is aan (2, 9). Ons doen dieselfde vir die tweede oplossing, en dit gee ons die snypunt (-3, 4) aan.Wenke
- Vergelykings vir `n sirkel of ellips het `n
termyn en a
termyn. Om die snypunt van `n sirkel en `n reguit lyn te vind, los vir x binne die lineêre vergelyking op. Vervang die oplossing vir x in die sirkelvergelyking, en die kwadratiese vergelyking het net baie makliker geword. Hierdie probleme kan 0, 1 of 2 oplossings hê, soos reeds in die metodes hierbo aangedui.
- `n Sirkel en `n parabool (of enige ander kwadratiese vergelyking) kan 0, 1, 2, 3 of 4 oplossings hê. Vind die veranderlike wat `n vierkant in beide vergelykings is — kom ons sê dit is x. los
aan en vervang die antwoord
in die ander vergelyking. Los y op om die 0, 1 of 2 oplossings te vind. Prop elke oplossing terug in die oorspronklike kwadratiese vergelyking en los vir x op. Elkeen van hierdie kan 0, 1 of 2 oplossings hê.
Artikels oor die onderwerp "Bereken die snypunt van twee lyne"
Оцените, пожалуйста статью
Soortgelyk
Gewilde