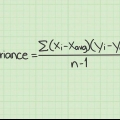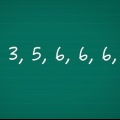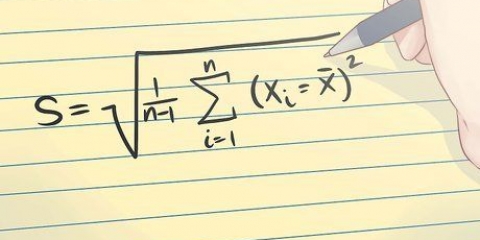Berekening van die som van vierkante (sse)

Inhoud

Trappe

Die som van vierkante, of SSE, is `n voorlopige statistiese berekening wat lei tot verskillende datawaardes. Wanneer jy `n stel datawaardes het, is dit nuttig om te kan bepaal hoe nou hierdie waardes aan mekaar verband hou. Jy moet jou data in `n tabel organiseer en dan `n paar redelik eenvoudige berekeninge doen. Sodra jy die SSE vir `n datastel gevind het, kan jy die afwyking en standaardafwyking vind.

Trappe

Metode 1 van 3: Bereken die SSE met die hand

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 1

1. Maak `n tabel van drie kolomme. Die maklikste manier om die SSE te bereken, is om met `n tabel van drie kolomme te begin. Benoem die drie kolomme

Waar die

${displaystyle {text{Waarde}}}$ ,

afwyking

${displaystyle {text{Afwyking}}}$ , en

afwyking 2

${displaystyle {text{Afwyking}}^{2}}$ .

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 2

2. Vul die besonderhede in. Die eerste kolom bevat die waardes van jou metings. Vul die kolom

Waar die

${displaystyle {text{Waarde}}}$ met jou lesings. Dit kan die resultate van `n eksperiment, `n statistiese studie of net data van `n wiskundeprobleem wees.

In hierdie geval, veronderstel jy werk met mediese data en jy het `n lys van die liggaamstemperature van tien pasiënte. Die verwagte normale liggaamstemperatuur is 98,6 grade. Die temperatuur van tien pasiënte word gemeet en gee die waardes 99.0, 98.6, 98.5, 101.1, 98.3, 98.6, 97.9, 98.4, 99.2 en 99.1. Die temperatuur van tien pasiënte word gemeet en gee die waardes 99.0, 98.6, 98.5, 101.1, 98.3, 98.6, 97.9, 98.4, 99.2 en 99.1. Skryf hierdie waardes in die eerste kolom.

Prent getiteld Bereken die som van vierkante vir fout (SSE) Stap 3

3. Bereken die gemiddelde. Voordat jy die fout vir elke meting kan bereken, moet jy die gemiddelde van die hele datastel bereken.

Die gemiddelde van `n datastel is die som van sy waardes gedeel deur die aantal waardes in die stel. Dit kan simbolies voorgestel word, met die veranderlike

μ

$mu$ :

μ = Σ X n

${displaystyle mu ={frac {Sigma x}{n}}}$

Vir hierdie data word die gemiddelde soos volg bereken:

μ = 99, 0 + 98, 6 + 98, 5 + 101, 1 + 98, 3 + 98, 6 + 97, 9 + 98, 4 + 99, 2 + 99, 1 10

${displaystyle mu ={frac {99.0+98.6+98.5+101.1+98.3+98.6+97.9+98.4+99.2+99.1} {10}}}$

μ = 988, 7 10

${displaystyle mu ={frac {988.7}{10}}}$

μ = 98, 87

${displaystyle mu =98.87}$

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 4

4. Bereken die individuele foutwaardes. In die tweede kolom van u tabel moet u die foutwaardes vir elke datawaarde invoer. Die fout is die verskil tussen die lesing en die gemiddelde.

Vir die gegewe datastel, trek die gemiddelde, 98.87, van elke gemete waarde af, en vul die tweede kolom in met die resultate. Hierdie tien berekeninge lyk soos volg:

99, 0 - 98, 87 = 0, 13

${displaystyle 99.0-98.87=0.13}$

98, 6 - 98, 87 = - 0, 27

${displaystyle 98.6-98.87=-0.27}$

98, 5 - 98, 87 = - 0, 37

${displaystyle 98.5-98.87=-0.37}$

101, 1 - 98, 87 = 2, 23

${displaystyle 101.1-98.87=2.23}$

98, 3 - 98, 87 = - 0, 57

${displaystyle 98.3-98.87=-0.57}$

98, 6 - 98, 87 = - 0, 27

${displaystyle 98.6-98.87=-0.27}$

97, 9 - 98, 87 = - 0, 97

${displaystyle 97.9-98.87=-0.97}$

98, 4 - 98, 87 = - 0, 47

${displaystyle 98.4-98.87=-0.47}$

99, 2 - 98, 87 = 0, 33

${displaystyle 99.2-98.87=0.33}$

99, 1 - 98, 87 = 0, 23

${displaystyle 99.1-98.87=0.23}$

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 5

5. Bereken die SSE. In die derde kolom van die tabel, vind die vierkant van elk van die resulterende waardes in die middelste kolom. Dit verteenwoordig die vierkante van die afwyking van die gemiddelde vir elke gemete datawaarde.

Vir elke waarde in die middelste kolom, gebruik `n sakrekenaar om die vierkant te bereken. Teken die resultate in die derde kolom soos volg aan:

0, 13 2 = 0, 0169

${displaystyle 0.13^{2}=0.0169}$

(- 0, 27) 2 = 0, 0729

${displaystyle (-0.27)^{2}=0.0729}$

(- 0, 37) 2 = 0, 1369

${displaystyle (-0.37)^{2}=0.1369}$

2, 23 2 = 4, 9729

${displaystyle 2.23^{2}=4.9729}$

(- 0, 57) 2 = 0, 3249

${displaystyle (-0.57)^{2}=0.3249}$

(- 0, 27) 2 = 0, 0729

${displaystyle (-0.27)^{2}=0.0729}$

(- 0, 97) 2 = 0, 9409

${displaystyle (-0.97)^{2}=0.9409}$

(- 0, 47) 2 = 0, 2209

${displaystyle (-0.47)^{2}=0.2209}$

0, 33 2 = 0, 1089

${displaystyle 0.33^{2}=0.1089}$

0, 23 2 = 0, 0529

${displaystyle 0.23^{2}=0.0529}$

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 6

6. Tel die vierkante van die foute bymekaar. Die laaste stap is om die som van die waardes in die derde kolom te vind. Die gewenste resultaat is die SSE, of die som van die kwadrate van die foute.

Vir hierdie datastel word die SSE bereken deur die tien waardes in die derde kolom by te voeg:

s s E = 6, 921

${displaystyle SSE=6.921}$

Metode 2 van 3: Skep `n Excel-sigblad om die SSE te bereken

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 7

1. Benoem die kolomme van die sigblad. Jy skep `n tabel met drie kolomme in Excel, met dieselfde drie opskrifte as hierbo.

In sel A1, tik `Waarde` as opskrif.
In blokkie B1, tik `Afwyking` as opskrif.
In blokkie C1, tik `Afwyking kwadraat` as opskrif.

Prent getiteld Bereken die som van vierkante vir fout (SSE) Stap 8

2. Voer jou besonderhede in. In die eerste kolom moet u die waardes van u metings invoer. As die stel klein is, kan jy dit maklik met die hand intik. As jy `n groot datastel het, moet jy dalk die data kopieer en in die kolom plak.

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 9

3. Bepaal die gemiddelde van die datapunte. Excel het `n funksie wat die gemiddelde vir jou bereken. In `n leë sel onder jou datatabel (dit maak nie saak watter sel jy kies nie), voer in:

=Gemiddeld(A2:___)

Moenie leë spasie tik nie. Vul daardie spasie in met die selnaam van jou laaste datapunt. Byvoorbeeld, as jy 100 datapunte het, sal jy die funksie gebruik:

=Gemiddeld(A2:A101)

Hierdie funksie bevat die data van selle A2 tot A101, want die boonste ry bevat die kolomopskrifte.

Wanneer jy Enter druk of na `n ander sel in die tabel klik, word die nuut geprogrammeerde sel outomaties gevul met die gemiddelde van jou datawaardes.

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 10

4. Voer die foutmetingsfunksie in. In die eerste leë sel in die `Afwyking`-kolom, moet jy `n funksie invoer om die verskil tussen elke datapunt en die gemiddelde te bereken. Om dit te doen, gebruik die selnaam waar die gemiddelde geleë is. Kom ons neem aan dat jy sel A104 vir nou gebruik het.

Die foutberekeningsfunksie, wat jy in sel B2 invoer, is:

=A2-$A$104. Die dollartekens is nodig om seker te maak jy sluit boks A104 vir elke berekening.

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 11

5. Vul die funksie vir die kwadraatfoute in. In die derde kolom kan jy Excel opdrag gee om die verlangde vierkant te bereken.

Voer die volgende funksie in sel C2 in:

=B2^2

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 12

6. Kopieer die funksies om die hele tabel te vul. Nadat u die funksies in die boonste sel van elke kolom, onderskeidelik B2 en C2 ingevoer het, moet u die hele tabel invul. Jy kan die funksie in elke reël van die tabel oortik, maar dit sal heeltemal te lank neem. Gebruik jou muis, merk selle B2 en C2 saam, en sleep sonder om die muisknoppie te los na die onderste sel van elke kolom.

Gestel jy het 100 datapunte in jou tabel, sleep jou muis na selle B101 en C101.

Wanneer jy die muisknoppie los, word die formules na alle selle van die tabel gekopieer. Die tabel moet outomaties gevul word met die berekende waardes.

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 13

7. Vind die SSE. Kolom C van jou tabel bevat alle kwadraat foutwaardes. Die laaste stap is om Excel die som van hierdie waardes te laat bereken.

In `n sel onder die tabel, waarskynlik C102 in hierdie voorbeeld, voer die volgende funksie in:

=Som(C2:C101)

Deur op Enter te klik of weg te klik in `n ander sel van die tabel sal jy die SSE-waarde van jou data gee.

Metode 3 van 3: Verwant aan SSE met ander statistiese data

Prent getiteld Bereken die som van vierkante vir foute (SSE) Stap 14

1. Bereken die afwyking van die SSE. Om die SSE vir `n datastel te vind is oor die algemeen `n bousteen om ander, meer bruikbare waardes te vind. Die eerste hiervan is variansie. Die variansie is `n maatstaf wat aandui hoeveel die gemete data van die gemiddelde afwyk. Dit is eintlik die gemiddelde van die kwadraatverskille van die gemiddelde.

Aangesien die SSE die som van die kwadraatfoute is, kan jy die gemiddelde (dit is die variansie) vind deur net deur die aantal waardes te deel. As jy egter die variansie van `n steekproefstel, eerder as `n hele populasie, bereken, deel jy die variansie deur (n-1) in plaas van n. Dus:

Variansie = SSE/n, as jy die variansie van `n hele populasie bereken.
Variansie = SSE/(n-1), as jy die variansie van `n steekproef van data bereken.

Vir die steekproefprobleem van die pasiënte se temperatuur, kan ons aanvaar dat 10 pasiënte slegs `n steekproef uitmaak. Daarom word die variansie dan soos volg bereken:

Variansie = SSE (n - 1)

${displaystyle {text{Variation}}={frac {text{SSE}}{(n-1)}}}$

Variansie = 6, 921 9

${displaystyle {text{Variation}}={frac {6,921}{9}}}$

Variansie = 0, 769

${displaystyle {text{Variation}}=0.769}$

Prent getiteld Bereken die som van vierkante vir fout (SSE) Stap 15

2. Bereken die standaardafwyking van die SSE. Die standaardafwyking is `n algemeen gebruikte waarde wat aandui hoeveel die waardes van `n datastel van die gemiddelde afwyk. Die standaardafwyking is die vierkantswortel van die variansie. Let daarop dat die variansie die gemiddeld van die kwadraat foutmate is.

Daarom, nadat jy die SSE bereken het, kan jy die standaardafwyking soos volg vind:

standaard afwyking = \sqrt{SSE} n - 1

${displaystyle {text{Standaardafwyking}}={sqrt {frac {text{SSE}}{n-1}}}}$

Vir die voorbeeld van die temperatuurmetings kan u die standaardafwyking soos volg vind:

standaard afwyking = \sqrt{SSE} n - 1

${displaystyle {text{Standaardafwyking}}={sqrt {frac {text{SSE}}{n-1}}}}$

standaard afwyking = \sqrt{\frac{6,921}{9}}

${displaystyle {text{Standard Deviation}}={sqrt {frac {text{6,921}}{9}}}}$

standaard afwyking = \sqrt{0, 769}

${displaystyle {text{Standaardafwyking}}={sqrt {0.769}}}$

standaard afwyking = 0, 877

${displaystyle {text{Standaardafwyking}}=0.877}$

Prent getiteld Bereken die som van vierkante vir fout (SSE) Stap 16

3. Gebruik SSE om die kovariansie te bepaal. Hierdie artikel het gefokus op datastelle wat slegs `n enkele waarde op `n slag meet. In baie studies kan jy egter twee afsonderlike waardes vergelyk. Byvoorbeeld, jy wil weet hoe daardie twee waardes met mekaar verband hou, nie net met die gemiddelde van die datastel nie. Hierdie waarde is die kovariansie.

Die berekeninge vir kovariansie is te gedetailleerd om hier beskryf te word, behalwe om daarop te let dat jy die SSE vir elke datatipe sal gebruik en dit dan vergelyk. Vir `n meer gedetailleerde beskrywing van die kovariansie en die betrokke berekeninge, sien vind artikels oor hierdie onderwerp op wikiHow.

As `n voorbeeld van die gebruik van kovariansie, kan u die ouderdom van die pasiënte in `n mediese studie vergelyk met die doeltreffendheid van `n geneesmiddel om die koorstemperatuur te verlaag. Dan het jy een datastel van ouderdomme en `n tweede datastel van temperature. Jy kry dan die SSE vir elke datastel, en van daar af die variansie, standaardafwykings en kovariansie.