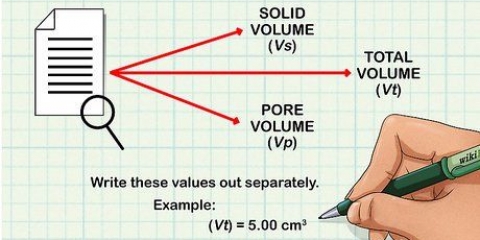
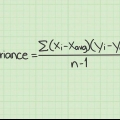In die data-insamelingsvoorbeeld word hierdie afwykings: 







Om die geldigheid van u berekeninge na te gaan, kyk ons of die som van die waardes in die kolom van afwykings gelyk is aan nul. As jy al die afwykings bymekaartel en jy kry iets anders as nul, dan is jou gemiddelde verkeerd, of jy het `n fout gemaak in die berekening van een of meer van die afwykings. Keer terug en kontroleer jou werk. 
Absolute waarde is `n wiskundige hulpmiddel om afstand of grootte aan te dui, ongeag die rigting. Om die absolute waarde te bepaal, laat eenvoudig die minusteken vir elke getal in die tweede kolom weg. Vul dus die derde kolom met die absolute waardes soos volg: 









Vir hierdie datastel sal die finale berekening wees: 

Byvoorbeeld, met hierdie datastel kan jy sê dat die gemiddelde nege is en die gemiddelde afstand vanaf die gemiddelde is 2,75. Let daarop dat sommige waardes nader as 2,75 is in vergelyking met ander. Maar 2.75 is die gemiddelde afstand.
Bereken die gemiddelde afwyking van die gemiddelde
Inhoud
As u met data werk, is daar verskeie maniere om te meet hoe nou u datawaardes gegroepeer is. Die mees algemene is die gemiddelde. Die meeste mense leer om die gemiddelde vroeg op skool te bereken deur die som van `n groep datawaardes te vind en dan te deel deur die aantal waardes in die groep. `n Meer gevorderde berekening is die gemiddelde afwyking oor die gemiddelde. Hierdie berekening vertel jou hoe naby jou waardes aan die gemiddelde is. Jy bepaal dit deur die gemiddelde van `n datastel te vind, dan die afwyking van elke data van daardie gemiddelde, en dan die gemiddelde van daardie afwykings.
Trappe
Deel 1 van 2: Berekening van die gemiddelde

1. Versamel en tel jou data. Vir enige stel waardes is die gemiddelde `n maatstaf van die sentrale waarde. Afhangende van die tipe data, sal die gemiddelde vir jou die middelwaarde van daardie data gee. Om die gemiddelde te vind, moet jy eers jou data insamel, hetsy deur `n eksperiment of net gegee dit op `n opdrag.
- As voorbeeld gebruik ons `n gegewe getalreeks 6, 7, 10, 12, 13, 4, 8 en 12. Hierdie ry is klein genoeg om met die hand te tel, en vinnig te sien dat dit `n ry van agt getalle is.
- Binne die statistiek, die veranderlike
of
word dikwels gebruik om die aantal waardes in `n reeks of versameling aan te dui.

2. Vind die som van die waardes. Die eerste stap in die bepaling van die gemiddelde is om die som van alle waardes te bereken. Binne statistiese notasie word elke waarde gewoonlik deur die veranderlike verteenwoordig  . Die som van alle waardes word die simbool gegee
. Die som van alle waardes word die simbool gegee  . Die Griekse hoofletter sigma dui aan dat dit die som van die waardes is. Die berekening vir hierdie eenvoudige reeks gaan soos volg:
. Die Griekse hoofletter sigma dui aan dat dit die som van die waardes is. Die berekening vir hierdie eenvoudige reeks gaan soos volg:
 . Die som van alle waardes word die simbool gegee
. Die som van alle waardes word die simbool gegee  . Die Griekse hoofletter sigma dui aan dat dit die som van die waardes is. Die berekening vir hierdie eenvoudige reeks gaan soos volg:
. Die Griekse hoofletter sigma dui aan dat dit die som van die waardes is. Die berekening vir hierdie eenvoudige reeks gaan soos volg:

3. Deel om die gemiddelde te vind. Ten slotte, deel die som deur die aantal waardes. Die Griekse letter mu,  , word dikwels gebruik om die gemiddelde aan te dui. Die berekening van die gemiddelde verloop dus soos volg:
, word dikwels gebruik om die gemiddelde aan te dui. Die berekening van die gemiddelde verloop dus soos volg:
 , word dikwels gebruik om die gemiddelde aan te dui. Die berekening van die gemiddelde verloop dus soos volg:
, word dikwels gebruik om die gemiddelde aan te dui. Die berekening van die gemiddelde verloop dus soos volg:
Deel 2 van 2: Vind die gemiddelde afwyking

1. Skep `n tabel. Om jou data in orde te hou en om te help met die berekeninge, is dit nuttig om `n tabel van drie kolomme te skep. Benoem die eerste kolom  . Benoem die tweede kolom
. Benoem die tweede kolom  . Benoem die derde kolom
. Benoem die derde kolom  .
.
 . Benoem die tweede kolom
. Benoem die tweede kolom  . Benoem die derde kolom
. Benoem die derde kolom  .
. - Vul die eerste kolom met die waardes vir jou berekening.

2. Bereken die afwyking (afwyking) van elke waarde. In die tweede kolom, gemerk  , stel die afwyking of verskil tussen elke waarde en die gemiddelde van die reeks of versameling. Vind hierdie waarde deur die gemiddelde van elke datawaarde af te trek.
, stel die afwyking of verskil tussen elke waarde en die gemiddelde van die reeks of versameling. Vind hierdie waarde deur die gemiddelde van elke datawaarde af te trek.
 , stel die afwyking of verskil tussen elke waarde en die gemiddelde van die reeks of versameling. Vind hierdie waarde deur die gemiddelde van elke datawaarde af te trek.
, stel die afwyking of verskil tussen elke waarde en die gemiddelde van die reeks of versameling. Vind hierdie waarde deur die gemiddelde van elke datawaarde af te trek.








3. Bepaal die absolute waarde van elke afwyking. Wanneer jy die afwyking van elke waarde van die gemiddelde bereken, wil jy net die verskil weet, nie of daardie verskil positief of negatief is nie. Wat jy regtig nodig het, in wiskundige terme, is die absolute waarde van die verskil. Die absolute waarde word deur vertikale stawe| aangedui |.










4. Bereken die gemiddelde van die absolute afwykings. Nadat u die driekolomtabel voltooi het, vind die gemiddelde van die absolute waardes in die derde kolom. Net soos jy gedoen het om die gemiddelde van die aanvanklike waardes te bereken, tel die afwykings bymekaar en deel die som deur die aantal waardes.


5. Interpreteer die resultaat. Die waarde van die gemiddelde afwyking van die gemiddelde is `n maatstaf van hoe naby die waardes aan mekaar is. Dit beantwoord die vraag: "Hoe naby aan die gemiddelde is die datawaardes gemiddeld?"?`
Wenke
- Hou aan oefen en jy sal dit glad kan bereken.
Artikels oor die onderwerp "Bereken die gemiddelde afwyking van die gemiddelde"
Оцените, пожалуйста статью
Gewilde