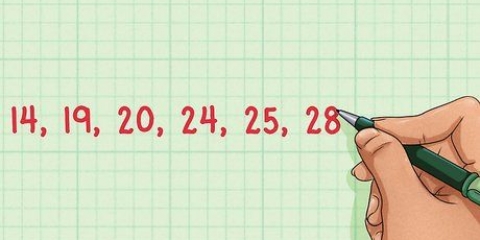Berekening van kumulatiewe frekwensie: 11 stappe (met prente)

Inhoud

Trappe
- Deel 1 van 2: Bepaling van fundamentele kumulatiewe frekwensie
- Deel 2 van 2: Doen meer met die data
Wenke

In statistieke verwys absolute frekwensie na die aantal kere wat `n gegewe waarde in `n datastel vertoon word. Kumulatiewe frekwensie is anders: dit is die som (of voorlopige totaal) van alle frekwensies tot by die huidige punt in die datastel. Moenie bekommerd wees as dit soos slang klink nie; dit is maklik as jy `n pen en papier gryp.

Trappe

Deel 1 van 2: Bepaling van fundamentele kumulatiewe frekwensie

Prent getiteld Bereken kumulatiewe frekwensie Stap 01

1. Sorteer die datastel. `n `datastel` is net die groep getalle wat jy bestudeer. Sorteer hierdie waardes van die kleinste na die grootste.

Voorbeeld: Jou datastel bevat die aantal boeke wat elke student die afgelope maand gelees het. Na sortering is dit die datastel: 3, 3, 5, 6, 6, 6, 8.

Prent getiteld Bereken kumulatiewe frekwensie Stap 02

2. Tel die absolute frekwensie van elke waarde. Die frekwensie van `n waarde is die aantal kere wat die waarde vertoon word (jy kan dit die `absolute frekwensie` noem as jy verwarring met kumulatiewe frekwensie wil vermy). Die maklikste manier om tred te hou daarvan is om `n tabel te skep. Tik "Waarde" (of `n beskrywing van wat die waarde meet) aan die begin van die eerste kolom. Skryf `Frekwensie` boaan die tweede kolom. Vul die tabel vir elke waarde in.

Voorbeeld: `Aantal boeke` boaan die eerste kolom. Skryf `Frekwensie` boaan die tweede kolom.

In die tweede ry, skryf die eerste waarde onder Aantal boeke: 3.

Tel die aantal drieë in jou datastel. Aangesien daar twee drieë is, tik 2 onder frekwensie in dieselfde ry.

Herhaal vir elke waarde totdat jy die hele tabel voltooi het:

3 | F=2

5 | F=1

6 | F=3

8 | F=1

Prent getiteld Bereken kumulatiewe frekwensie Stap 03

3. Bepaal die kumulatiewe frekwensie van die eerste waarde. Die kumulatiewe frekwensie beantwoord die vraag `hoeveel keer kom hierdie waarde? of `n kleiner waarde vir?Begin altyd met die laagste waarde in jou datastel. Aangesien daar geen kleiner waardes is nie, is die antwoord dieselfde as die absolute frekwensie van daardie waarde.

Voorbeeld: Die laagste waarde is drie. Die aantal studente wat drie boeke gelees het, is twee. Niemand het minder boeke gelees nie, so die kumulatiewe frekwensie is drie. Voeg dit by die eerste ry van jou tabel:

3 | F=2 | CF=2

Prent getiteld Bereken kumulatiewe frekwensie Stap 04

4. Bepaal die kumulatiewe frekwensie van die volgende waarde. Gaan voort na die volgende waarde in die tabel. Ons het pas uitgevind hoeveel keer die laer waardes voorkom. Om die kumulatiewe frekwensie van hierdie waarde te bepaal, hoef ons net die absolute frekwensie by die lopende totaal te voeg. Met ander woorde, neem die laaste kumulatiewe frekwensie wat jy gevind het, en voeg die absolute frekwensie van hierdie waarde daarby.

Voorbeeld:

3 | F=2 | CF=2

5 | F=1 | CF=2+1=3

Prent getiteld Bereken kumulatiewe frekwensie Stap 05

5. Herhaal vir die ander waardes. Gaan voort met groter en groter waardes. Tel elke keer die laaste kumulatiewe frekwensie by die absolute frekwensie van die volgende waarde.

Voorbeeld:

3 | F=2 | CF=2

5 | F=1 | CF=2 + 1=3

6 | F=3 | CF=3 + 3=6

8 | F=1 | CF=6 + 1=7

Prent getiteld Bereken kumulatiewe frekwensie Stap 06

6. Gaan jou werk na. Sodra jy klaar is, het jy die aantal gevalle van elke veranderlike opgetel. Die laaste kumulatiewe frekwensie moet gelyk wees aan die totale aantal datapunte in die reeks. Daar is twee maniere om dit na te gaan:

Tel individuele frekwensies by: 2 + 1 + 3 + 1=7, ons laaste kumulatiewe frekwensie.

Tel die aantal datapunte. Ons lys was 3, 3, 5, 6, 6, 6, 8. Daar is sewe voorwerpe, ons uiteindelike kumulatiewe frekwensie.

Deel 2 van 2: Doen meer met die data

Prent getiteld Bereken kumulatiewe frekwensie Stap 07

1. Verstaan diskrete en deurlopende data. Diskrete data kom in eenhede wat jy kan tel, waar dit onmoontlik is om `n deel van `n eenheid te bepaal. Deurlopende data beskryf iets wat nie getel kan word nie, met metings wat iewers tussen die eenhede wat jy gekies het kan val. Hier is `n paar voorbeelde:

Aantal honde: Diskreet. Daar is nie iets soos `n halwe hond nie.
Sneeudiepte: aaneenlopend. Sneeu bou geleidelik op, nie in een eenheid op `n slag nie. As jy dit in sentimeter probeer meet het, het jy dalk `n laag sneeu gevind van 5,6 sentimeter diep.

Prent getiteld Bereken kumulatiewe frekwensie Stap 08

2. Groepeer deurlopende data volgens reeks. Deurlopende datastelle het dikwels `n groot aantal unieke veranderlikes. Om die metode hierbo te probeer gebruik, sal die tabel baie lank en moeilik maak om te verstaan. Maak eerder elke reël van jou tabel `n reeks waardes. Dit is belangrik dat elke reeks dieselfde grootte is (soos 0-10, 11- 20, 21-30, ens.), maak nie saak hoeveel waardes in elke reeks teenwoordig is nie. Hier is `n voorbeeld van `n deurlopende datastel wat in `n tabel gemaak is:

Datastel: 233, 259, 277, 278, 289, 301, 303

Tabel (eerste kolom -- waarde, tweede kolom -- frekwensie, derde kolom -- kumulatiewe frekwensie):

200–250|1|1

251–300|4|1 + 4=5

301–350|2|5 + 2=7

3. Skep `n grafiek. Sodra jy die kumulatiewe frekwensie bereken het, gryp grafiekpapier. Teken `n grafiek waar die x-as gelyk is aan die waardes van jou datastel, en die y-as gelyk is aan die kumulatiewe frekwensie. Dit sal die volgende berekeninge baie makliker maak.

Byvoorbeeld: As jou datastel van 1 na 8 gaan, teken `n x-as met agt eenhede daarop gemerk. Teken op elke waarde van die x-as `n punt op die y-waarde wat gelyk is aan die kumulatiewe frekwensie op daardie punt. Verbind elke paar aangrensende punte met `n lyn.

As daar geen datapunte op `n gegewe waarde is nie, dan is die absolute frekwensie nul. Deur nul by die laaste kumulatiewe frekwensie te voeg sal nie die waarde verander nie, daarom teken ons `n punt by dieselfde y-waarde as die laaste waarde.

Aangesien kumulatiewe frekwensie altyd saam met die waardes toeneem, moet jou grafiek altyd stabiel bly of styg soos dit na regs beweeg. As die lyn een of ander tyd afgaan, kan jy per ongeluk na `n absolute frekwensie kyk.

Prent getiteld Bereken kumulatiewe frekwensie Stap 10

4. Vind die mediaan van die grafiek. Die mediaan is die waarde wat presies in die middel van die datastel is. Die helfte van die waardes is bo die mediaan, en die ander helfte daaronder. Hier is hoe om die mediaan in jou grafiek te vind:

Kyk na die laaste punt aan die regterkant van die grafiek. Die y-waarde is die totale kumulatiewe frekwensie, wat die aantal punte in die datastel is. Gestel hierdie waarde is gelyk aan 16.

Vermenigvuldig hierdie waarde met ½ en vind dit op die y-as. In ons voorbeeld is dit 8 (die helfte van 16). Vind 8 op die y-as.

Vind die punt op die grafiek by hierdie y-waarde. Beweeg jou vinger vanaf die 8 op die y-as langs die grafiek. Stop wanneer jou vinger die lyn van die grafiek raak. Dit is die punt waar presies die helfte van jou datapunte getel word.

Bepaal die x-waarde op hierdie punt. Beweeg jou vinger reguit af na die x-as. Hierdie waarde is die mediaan van jou datastel. Byvoorbeeld, as hierdie waarde 65 is, is die helfte van jou datastel onder 65 en die helfte is bo 65.

Prent getiteld Bereken kumulatiewe frekwensie Stap 11

5. Bepaal die kwartiele vanaf die grafiek. Kwartiele verdeel die data in vier afdelings. Hierdie proses is baie soortgelyk aan die bepaling van die mediaan. Die enigste verskil is hoe jy die y-waardes bepaal:

Om die y-waarde van die onderste kwartiel te vind, neem die maksimum kumulatiewe frekwensie en vermenigvuldig dit met ¼. Die ooreenstemmende x-waarde sal jou die y-waarde gee, met presies `n kwart van die data daaronder.

Om die y-waarde van die boonste kwartiel te vind, vermenigvuldig die maksimum kumulatiewe frekwensie met ¾. Die ooreenstemmende x-waarde sal vir jou die y-waarde gee, met presies driekwart van die data daaronder en `n kwart bo dit.