Let egter daarop dat as die tydeenhede wat in jou gemiddelde spoedwaarde gebruik word, verskil van dié in jou tydwaarde, jy die een of die ander moet omskakel om te pas. Byvoorbeeld, as `n gemiddelde spoed gemeet word in km/h en die tyd is in minute, sal jy die tyd deur 60 moet deel om dit na ure om te skakel. Kom ons los ons voorbeeldprobleem op. 120 km/h × 0,5 h = 60 km. Let daarop dat die tydeenhede (ure) wegval teenoor die eenhede in die noemer van die gemiddelde spoed (ure), wat slegs die eenhede van afstand (km) laat. 
Gestel ons weet dat `n motor 60 km in 50 minute afgelê het, maar ons het geen waarde vir die gemiddelde spoed terwyl jy bestuur nie. In hierdie geval kan ons die veranderlike s gebruikjuweel isoleer in die basisvergelyking vir die afstand, en ons kry sjuweel = d/t te kry. Dan bereken ons 60 km/50 minute = 1,2 km/min. Let daarop dat ons antwoord vir spoed in ons voorbeeld `n ongewone eenheid het (km/minuut). Om jou antwoord in die meer algemene vorm van km/hr te kry, vermenigvuldig dit met 60 minute/hr en kry `72 km/h om te kry. 
Voorbeeld: In die voorbeeldprobleem hierbo het ons tot die gevolgtrekking gekom dat om 60 km in 50 minute te reis, ons teen 72 km/h sal moet reis. Dit is egter net waar as ons vir die hele reis teen een spoed ry. Byvoorbeeld, deur die helfte van die rit teen 80 km/h en die ander helfte teen 64 km/h te ry, ry ons steeds 60 km in 50 minute — 72 km/h = 60 km/50 min = ????? Wiskundige oplossings die gebruik van afgeleides is dikwels `n beter keuse as die afstandformule om die spoed van `n voorwerp in werklike situasies te definieer, want veranderinge in spoed is waarskynlik. 

Let daarop dat hierdie formule absolute waardes gebruik (die simbool |). Absolute waardes beteken eenvoudig dat die terme binne die simbole positief word wanneer hulle negatief is. Kom ons sê byvoorbeeld ons stop op `n perfek reguit stuk pad langs die pad. As daar `n klein dorpie 5 km voor ons is en `n stad 1 km agter ons, hoe ver is die twee stede uitmekaar?? As ons stad 1 as x neem1 = beskou 5 en stad 2 as x2 = -1, dan kan ons d, die afstand tussen die twee stede, soos volg vind: d = |x2 - X1| = |-1 - 5| = |-6| = 6 km. 
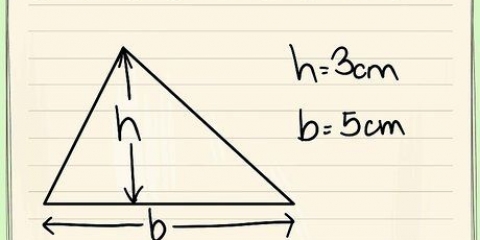
Die afstandformule in tweedimensionele ruimte gebruik die Pythagoras-stelling, wat sê dat die skuinssy van `n reghoekige driehoek gelyk is aan die vierkantswortel van die ander twee sye. Byvoorbeeld, kom ons sê ons het twee punte in die x-y-vlak: (3, -10) en (11, 7) wat onderskeidelik die middelpunt van `n sirkel en `n punt op die sirkel verteenwoordig. Om die reguit afstand tussen hierdie twee punte te vind, kan ons die volgende oplos: d = √((x2 - X1) + (j2 - y1)) d = √((11 - 3) + (7 - -10)) d = √(64 + 289) d = √(353) = 18.79 
Voorbeeld: Kom ons sê dit as `n ruimtevaarder wat naby twee asteroïdes in die ruimte sweef. Die een is so 8km voor ons, 2km regs van ons en 5km onder ons, terwyl die ander 3km agter ons, 3km links van ons en 4km bo ons is. As ons die posisies van hierdie asteroïdes voorstel met die koördinate (8.2,-5) en (-3,-3.4), kan ons die afstand tussen die twee soos volg vind: d = √((-3 - 8) + (-3 - 2) + (4 - -5)) d = √((-11) + (-5) + (9)) d = √(121 + 25 + 81) d = √(227) =15,07 km
Bereken afstand
Inhoud
Afstand, dikwels na verwys as die veranderlike d, is `n maatstaf van die spasie wat `n reguit lyn tussen twee punte inneem. Afstand kan verwys na die spasie tussen twee stilstaande punte (byvoorbeeld, `n persoon se hoogte is die afstand van die onderkant van sy of haar voete na die bokant van sy of haar kop) of kan verwys na die spasie tussen die huidige posisie van `n bewegende voorwerp en sy beginligging. Die meeste afstandsprobleme kan met die vergelykings opgelos word d = sjuweel × t waar d die afstand is, sjuweel die gemiddelde spoed, en t die tyd, of die vergelyking d = √((x2 - X1) + (j2 - y1)), waar (x1, y1) en (x2, y2) is die x- en y-koördinate van twee punte.
Trappe
Metode 1 van 2: Bepaal afstand met gemiddelde spoed en tyd

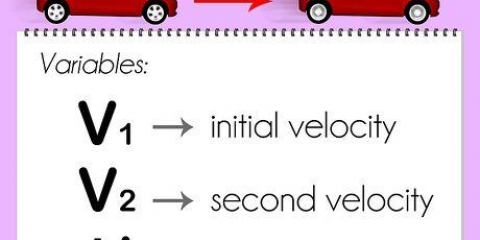
1. Bepaal die waardes vir gemiddelde spoed en tyd. Wanneer jy probeer om die afstand te vind wat `n bewegende voorwerp afgelê het, is twee stukke inligting noodsaaklik om hierdie berekening te maak: die spoed` (of snelheidsgrootte) en dietyd waarheen die voorwerp geskuif is. Met hierdie data is dit moontlik om die afstand wat die voorwerp afgelê het, te vind deur die formule d = s te gebruikjuweel × t.
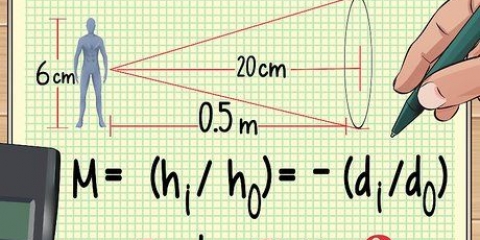
- Om die toepassing van die afstandformule beter te verstaan, gaan ons in hierdie afdeling `n voorbeeldprobleem oplos. Kom ons sê ons ry teen so 120 km/h en wil weet hoe ver ons oor `n halfuur gaan ry. Van 120 km/h as ons waarde vir die gemiddelde spoed en 0,5 uur as ons waarde vir tyd, sal ons hierdie probleem in die volgende stap oplos.

2. Vermenigvuldig die gemiddelde spoed met die tyd. Sodra jy die gemiddelde spoed van `n bewegende voorwerp ken en die tyd wat dit geneem het om te beweeg, is dit relatief maklik om die afstand te vind wat dit afgelê het. Vermenigvuldig net hierdie twee waardes saam om jou antwoord te kry.

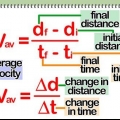
3. Redigeer die vergelyking om vir die ander veranderlikes op te los. Die eenvoud van die basiese afstandsvergelyking (d = sjuweel × t) maak dit redelik maklik om die vergelyking te gebruik om die waardes van veranderlikes bykomend tot afstand te vind. Isoleer die veranderlike wat jy wil oplos volgens die basiese reëls van wiskunde, en voer dan die waardes van die ander twee veranderlikes in om die waarde van die derde te vind. Met ander woorde, om die gemiddelde spoed van jou voorwerp te vind, gebruik die vergelyking sjuweel = d/t en om die tyd te vind wat `n voorwerp gereis het, gebruik die vergelyking t = d/sjuweel.

4. Let daarop dat die veranderlike `sjuweel` in die afstand verwys formule na gemiddeld spoed. Dit is belangrik om te verstaan dat die standaardafstandformule `n vereenvoudigde prentjie van `n voorwerp se beweging verskaf. Die afstandformule neem aan dat die bewegende voorwerp `n het konstante spoed het — met ander woorde, dit aanvaar dat die bewegende voorwerp teen `n `eenvormige`, onveranderlike spoed beweeg. Vir abstrakte wiskundeprobleme, soos dié wat in `n akademiese omgewing teëgekom word, is dit soms steeds moontlik om die beweging van `n voorwerp met behulp van hierdie aanname te modelleer. In die werklike lewe verteenwoordig hierdie model egter dikwels nie die beweging van bewegende voorwerpe akkuraat nie, wat in werklikheid mettertyd kan versnel, vertraag, stop en omkeer.
Metode 2 van 2: Bepaal die afstand tussen twee punte

1. Bepaling van twee punte in `n plat spasie. Wat as jy die afstand tussen twee stilstaande voorwerpe moet bepaal, in plaas daarvan om die afstand te bepaal wat `n bewegende voorwerp afgelê het? In gevalle soos hierdie sal die spoedgebaseerde afstandformule wat hierbo beskryf word, nie van enige nut wees nie. Gelukkig is daar nog `n afstandformule om vinnig die kortste afstand tussen twee punte te vind. Vir hierdie formule moet jy egter die koördinate van die twee punte ken. As jy met `n eendimensionele afstand te doen het (soos op `n getallelyn), is jou koördinate twee getalle, x1 en x2. As jy met afstand in twee dimensies te doen het, benodig jy waardes vir twee punte (x,y), (x)1,y1) en (x2,y2). Ten slotte, vir drie dimensies benodig u waardes vir (x1,y1,Z1) en (x2,y2,Z2).

2. Bepaal afstand op `n lyn deur die waarde van die koördinate vir die twee punte af te trek. Om die eendimensionele afstand tussen twee punte te bereken as jy weet wat die waarde vir elke punt is, is maklik. Gebruik net die formule d = |x2 - X1|. In hierdie formule trek jy x af1 af van x2 en neem die absolute waarde van jou antwoord om die afstand tussen x te vind1 en x2 te vind. Normaalweg gebruik jy die eendimensionele afstandformule wanneer die twee punte op `n getallelyn of -as lê.

3. Vind die afstand in die vliegtuig deur die Pythagoras-stelling te gebruik. Om afstand tussen twee punte in tweedimensionele ruimte te vind is meer ingewikkeld as in een dimensie, maar nie moeilik nie. Gebruik net die formule d = √((x2 - X1) + (j2 - y1)). In hierdie formule trek jy die twee x-koördinate af, vierkant die resultaat, trek die y-koördinate af, vierkant die resultaat, tel die twee tussenresultate by, en bereken die vierkantswortel om die afstand tussen die twee punte te vind. Hierdie formule werk in die tweedimensionele vlak - byvoorbeeld op die standaard x/y-kaarte.

4. Bepaal die driedimensionele afstand deur die oppervlakteformule te verander. In drie dimensies het punte ook `n z-koördinaat bykomend tot die x- en y-koördinaat. Om die afstand tussen twee punte in driedimensionele ruimte te vind, gebruik d = √((x2 - X1) + (j2 - y1) + (z2 - Z1)). Dit is `n gewysigde vorm van die tweedimensionele afstandsformule wat hierbo beskryf is wat ook die z-koördinate in ag neem. Deur die twee z-koördinate van mekaar af te trek, hulle vierkantig te maak en deur die res van die formule te hardloop soos hierbo beskryf, sal jy seker wees dat jou finale antwoord die driedimensionele afstand tussen die twee punte weerspieël.
Artikels oor die onderwerp "Bereken afstand"
Оцените, пожалуйста статью
Gewilde