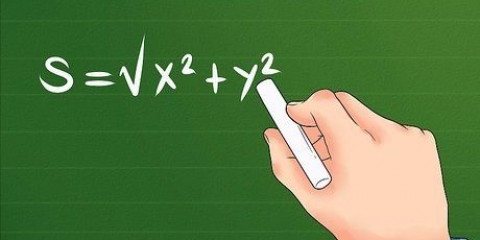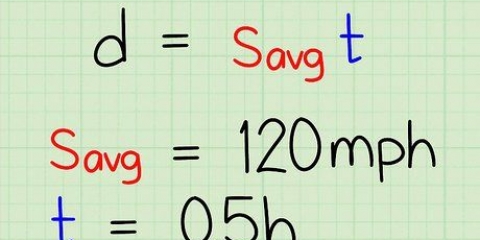Bereken spoed

Inhoud

Trappe
Wenke

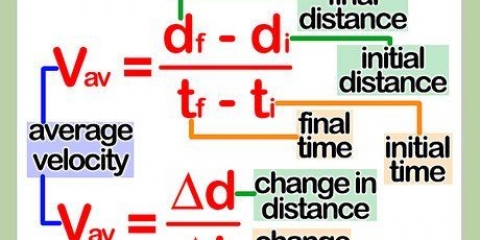
Spoed is die maatstaf van `hoe vinnig` iets op `n gegewe oomblik gaan. As jy al ooit na `n motor se spoedmeter gekyk het terwyl jy bestuur, het jy gesien hoe spoed gemeet word - hoe verder die naald gaan, hoe vinniger is die motor se spoed. Daar is `n paar verskillende maniere om spoed te bereken, afhangend van watter inligting jy het. Vir algemene doeleindes is die vergelyking spoed = afstand/tyd (of s = a/t) gewoonlik die maklikste manier om spoed te bereken.

Trappe

Metode 1 van 3: Gebruik die standaardspoedvergelyking

1. Vind die afstand wat `n voorwerp afgelê het. Die basiese vergelyking wat die meeste mense gebruik om uit te vind hoe vinnig iets gaan, is baie maklik om te gebruik. Die eerste ding wat jy moet weet is hoeveel afstand die voorwerp afgelê het. Met ander woorde, hoe ver is die beginpunt van die eindpunt af?

Hierdie vergelyking sal makliker wees om te verstaan met `n voorbeeld. Kom ons sê ons neem `n motorrit na `n pretpark van 100 myl (ongeveer 161 kilometer). In die volgende paar stappe sal ons hierdie inligting gebruik om hierdie vergelyking op te los.

2. Vind die tyd wat dit die voorwerp geneem het om daardie afstand te reis. Die volgende stukkie inligting wat jy nodig het is hoe lank dit die voorwerp geneem het om te reis. Met ander woorde, hoe lank het dit geneem om van die beginpunt na die eindpunt te kom?

In ons voorbeeld, kom ons sê dat dit presies is twee uur koste om hierdie reis te maak.

3. Deel die afstand deur die tyd om die spoed te vind. Al wat jy nodig het, is hierdie twee stukke inligting om jou spoed vir die reis te bepaal. Die afstand oor die tyd gee jou die spoed van die voorwerp.

In ons voorbeeld is hierdie vergelyking 100 myl/2 uur = 50 myl/uur(ongeveer 80 km/h).

4. Moenie die eenhede vergeet nie. Benoem jou antwoord met die toepaslike eenhede (soos myl per uur, ens.) is krities. Sonder eenhede kan dit vir ander mense moeilik wees om te verstaan wat jou antwoord beteken. Jy kan ook punte verloor as jy vergeet om die eenheid op `n skooltaak neer te skryf.

Die eenhede vir spoed is die eenhede van afstand oor die eenhede van tyd. In ons voorbeeld is ons eenhede myl/uur (of myl per uur) aangesien ons afstand in myl en tyd in ure gemeet het.

Metode 2 van 3: Los ander probleme op

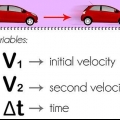
1. Isoleer die verskillende veranderlikes om afstand en tyd te bereken. Sodra jy die basiese beginsels van die spoedvergelyking ken, kan jy dit gebruik om meer as net spoed te vind. Byvoorbeeld, as jy die spoed en een van die ander veranderlikes ken, kan jy die vergelyking herrangskik om die ontbrekende stukkie inligting te vind.

Gestel ons weet dat `n trein vier uur lank teen `n spoed van 20 kilometer per uur gery het, maar ons moet weet watter afstand dit afgelê het. In hierdie geval kan ons die vergelyking herrangskik en dit op hierdie manier oplos:
spoed = afstand/tyd
spoed × tyd = (afstand/tyd) × tyd
spoed × tyd= afstand
20 km/h × 4 h = afstand = 80 kilometer

2. Skakel jou eenhede om indien nodig. Soms kan jy die spoed in `n ander eenheid bereken as wat jy nodig het. In hierdie geval moet jy omskakelingsfaktore gebruik om jou antwoord in die korrekte eenheid te plaas. Om dit te doen, skryf die verwantskappe tussen jou eenhede as `n breuk en vermenigvuldig. Wanneer jy vermenigvuldig, draai jy jou breuk soos nodig om ontslae te raak van die eenhede wat jy nie wil hê nie. Dit is baie makliker as wat dit klink!

Byvoorbeeld, kom ons sê dat in die voorbeeldprobleem hierbo ons ons antwoord nodig het in myl in plaas van kilometers. Daar is ongeveer 1,6 kilometer in `n myl, so ons kan dit so omskakel:

80 kilometer × 1 myl/1.6 kilometer = 50 myl

Let daarop dat omdat kilometers onderaan die breuk is, dit deurgehaal kan word met die kilometers in die oorspronklike antwoord, wat die antwoord in myl laat.

Hierdie een webwerf bevat omskakelings vir die mees algemene eenhede.

3. Vervang die veranderlike `afstand` met afstandformules indien nodig. Voorwerpe beweeg nie altyd in mooi, gerieflike reguit lyne nie. Indien nie, kan jy dalk nie bloot `n numeriese waarde vir afstand in die standaardspoedvergelyking invoeg nie. In plaas daarvan moet jy dalk die a in s = a/t vervang met `n formule wat die afstand modelleer wat die voorwerp afgelê het.

Byvoorbeeld, kom ons sê `n vliegtuig vlieg vyf keer in `n sirkel wat 20 myl breed is. Die vliegtuig voltooi hierdie reis in `n halfuur. In hierdie voorbeeld moet ons nog bepaal presies hoe ver die vliegtuig gereis het voordat ons die spoed kan vind. Ons kan die vergelyking gebruik vir die afstand om `n sirkel (sy omtrek) in plaas van "a" in ons vergelyking. Hierdie vergelyking is omtrek = 2πr waar r = die radius van die sirkel. Ons kan dit soos volg oplos:

s = (2 × π × r)/t

s = (2 × π × 10)/0.5

s = 62.83/0.5 = 125.66 myl/uur

4. Sien dat s = a/t a gemiddeld spoed gee. Die eenvoudige, gerieflike vergelyking wat ons gebruik het om spoed te vind, het een groot fout. Die waarde wat dit gee is tegnies `n gemiddelde spoed. Dit beteken dat dit aanvaar dat die voorwerp wat jy meet het dieselfde spoed regdeur die reis. Soos ons hieronder sal sien, kan dit moeiliker wees om die spoed van `n voorwerp op enige gegewe tydstip te vind.

Om hierdie verskil te illustreer, stel jou die laaste reis voor wat jy in `n motor geneem het. Dit is hoogs onwaarskynlik dat jy die hele reis dieselfde spoed gery het. In plaas daarvan het jy stadig begin en geleidelik jou topspoed bereik en stadiger gery by verkeersligte, verkeersknope, ensovoorts. As jy die standaardspoedvergelyking gebruik om jou spoed vir die rit te bereken, word hierdie spoedveranderinge nie weerspieël nie. In plaas daarvan sal jy iewers `n antwoord kry tussen die verskillende snelhede waarmee jy gereis het.

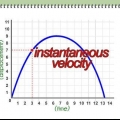
Metode 3 van 3: Berekening van oombliklike snelheid

Opmerking: Hierdie afdeling gebruik tegnieke wat onbekend is vir diegene wat nie calculus bestudeer het nie. Sien ons calculus-artikels vir hulp.

1. Let daarop dat spoed gedefinieer word as die grootte van die spoed. Hoër vlak snelheidsberekeninge kan verwarrend wees omdat wiskundiges en wetenskaplikes verskillende definisies vir "spoed" gebruik. `n Snelheid (snelheid) het twee komponente: a grootte en a rigting. Die grootte is gelyk aan die spoed van die voorwerp. `n Verandering van rigting sal `n verandering in snelheid (snelheid) veroorsaak, maar nie in snelheid nie.

Byvoorbeeld, kom ons sê twee motors ry in teenoorgestelde rigtings. Die spoedmeters van albei motors lees 50 km/h sodat hulle albei dieselfde spoed het. Aangesien hulle egter uitmekaar beweeg, kan ons sê dat een motor a spoed (snelheid) van -50 km/h en een het `n spoed (snelheid) vanaf 50 km/h.
Net soos jy die oombliklike snelheid (spoed) kan bereken, kan jy ook die Bereken oombliklike spoed (snelheid).

2. Gebruik absolute waardes vir negatiewe snelhede. Voorwerpe kan spoed van negatiewe grootte hê (as hulle in `n negatiewe rigting beweeg relatief tot iets anders). Daar is egter nie iets soos `n negatiewe snelheid (spoed) nie so in hierdie gevalle die absolute waarde van grootte verander die spoed van die voorwerp.

Om hierdie rede het beide motors in die voorbeeldprobleem hierbo `n spoed (spoed) deur 50 km/h.

3. Neem die afgeleide van `n posisiefunksie. As jy `n funksie s(t) het wat jou die posisie van `n voorwerp met betrekking tot tyd gee, dan sal die afgeleide van s(t) jou gee spoed (snelheid) gee met betrekking tot tyd. Prop net `n tydwaarde in hierdie vergelyking vir die veranderlike t (of wat ook al die tydwaarde is) om die spoed op hierdie punt te kry. Van hier af is dit maklik om die spoed te vind.

Gestel die posisie van `n voorwerp in meter word gegee deur die vergelyking 3t + t - 4 waar t = tyd in sekondes. Ons wil weet wat die spoed van die voorwerp is by t = 4 sekondes. In hierdie geval kan ons dit soos volg oplos:

3t + t - 4

s`(t) = 2 × 3t + 1

s`(t) = 6t + 1

Nou vul ons t = 4 in:

s`(t) = 6(4) + 1 = 24 + 1 = 25 meter/sekonde. Dit is tegnies `n snelheidsmeting (snelheid), maar aangesien dit positief is en rigting nie in die probleem genoem word nie, kan ons dit in wese vir snelheid gebruik.

4. Neem die integraal van `n versnellingsfunksie. Versnelling is `n manier om verandering in die spoed van `n voorwerp oor tyd te meet. Hierdie onderwerp is `n bietjie te kompleks om volledig in hierdie artikel te verduidelik. Dit is egter nuttig om daarop te let dat wanneer jy `n funksie a(t) het wat versnelling met betrekking tot tyd gee, die integraal van a(t) jou snelheid (snelheid) met betrekking tot tyd gee. Let daarop dat dit nuttig is om die aanvanklike snelheid van die voorwerp te ken sodat jy die konstante wat voortspruit uit `n onbepaalde integraal kan definieer.

Gestel `n voorwerp het `n konstante versnelling (in m/s gegee deur a (t) = -30. Kom ons sê ook dat die voorwerp `n beginsnelheid van 10 m/s het. Ons moet die spoed vind by t = 12s. In hierdie geval kan ons dit soos volg oplos:

a(t) = -30

v(t)= ∫ a(t)dt =∫ -30dt = -30t + C

Om C te vind, los ons op vir v(t) vir t = 0. Onthou dat die aanvanklike spoed van die voorwerp 10 m/s is.

v(0) = 10 = -30(0) + C

10 = C, dus v(t) = -30t + 10

Nou kan ons t = 12 sekondes invoer.

v(12) = -30(12) + 10 = -360 + 10 = -350. Aangesien snelheid die absolute waarde van snelheid is, is die snelheid van die voorwerp 350 meter/sekonde.

Wenke

Oefening maak perfek! Probeer om jou eie somme te maak deur verskillende getalle in die voorbeeldprobleme hierbo te vervang.
As jy op soek is na `n vinnige manier om te bereken vir gevorderde spoedberekeninge, gebruik hier as die aanlyn afgeleide sakrekenaar en die aanlyn integrale sakrekenaar hier.

Artikels oor die onderwerp "Bereken spoed"

Bereken kinetiese energie

Bereken vergroting

Bereken oombliklike spoed

Bereken versnelling

Оцените, пожалуйста статью