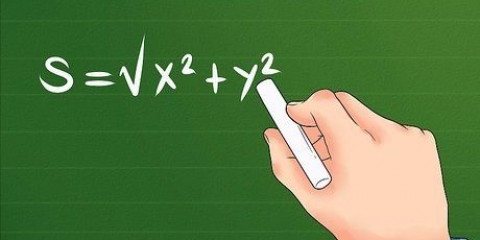Gratis stap vir stap instruksies 
In ons voorbeeldprobleem kan ons die lensvergelyking gebruik om d te vindi om te besluit. Vul die waardes van f en d inO en los op: Die brandpunt van `n lens is die afstand vanaf die middel van die lens tot by die punt waar die ligstrale in `n brandpunt konvergeer. As jy al ooit probeer het om `n gat in `n stuk papier met `n vergrootglas te brand, weet jy wat dit beteken. Hierdie waarde word dikwels gegee vir fisika probleme. In die werklike lewe sal jy soms hierdie inligting op die lens self gemerk vind. 
In ons voorbeeldprobleem bepaal ons hi soos volg: Let daarop dat `n negatiewe hoogte aandui dat die beeld wat ons sien omgekeer is. 
In ons voorbeeld bepaal ons M soos volg: Ons kry ook dieselfde antwoord as ons die d-waardes gebruik: Let daarop dat vergroting geen eenheid het nie. 
Die grootte. Hoe groter die absolute waarde van M, hoe meer sal die voorwerp deur die lens vergroot word. Die waardes van M tussen 1 en 0 dui aan dat die voorwerp kleiner sal lyk. Die oriëntasie. Negatiewe waardes dui aan dat die beeld onderstebo is. In ons voorbeeld is die waarde van M -0.666, wat beteken dat, onder die gegewe toestande, die beeld van die aksiepop onderstebo en twee derdes die normale grootte. 
Kom ons ondersoek bogenoemde probleem weer, net hierdie keer vir `n divergerende lens met `n brandpunt van -20 sentimeter. Alle ander voorletters is dieselfde. Eers bepaal ons di met die lensvergelyking: Nou bepaal ons hi en M met ons nuwe waarde vir di. 
Byvoorbeeld: veronderstel ons het `n klein teleskoop. As die brandpunt van die objektief 10 sentimeter is en die brandpunt van die oogstuk is 5 sentimeter, dan is die 10/5 = 2.
Bereken vergroting
Inhoud
In optika, die vergroting van `n voorwerp soos `n lens, die verhouding tussen die hoogte van die beeld van `n voorwerp wat jy kan sien en die werklike grootte daarvan. Byvoorbeeld, `n lens wat `n klein voorwerp groot laat lyk, het `n sterk vergroting, terwyl `n lens wat `n voorwerp kleiner laat lyk, a swak vergroting het. Die vergroting van `n voorwerp word gewoonlik deur die formule gegee M = (hi/hO) = -(di/dO), waar M = vergroting, hi = beeldhoogte, hO = voorwerphoogte, en di en dO =beeldafstand en voorwerpafstand.
Trappe
Metode 1 van 2: Bepaal die grootte van `n enkele lens
Let wel: A konvergerende lens is breër in die middel as aan die rand (soos `n vergrootglas). A divergerende lens is wyer by die rand en dunner in die middel (soos `n bak). Dieselfde reëls geld vir beide wanneer dit kom by die bepaling van vergroting, met een belangrike uitsondering, soos jy hieronder sal sien.
1. Neem die vergelyking/formule as `n beginpunt en bepaal watter data jy het. Soos met ander fisika-probleme, is `n goeie benadering om eers die vergelyking wat jy nodig het, neer te skryf. Dan kan jy begin soek na die ontbrekende stukke uit die vergelyking.
- Veronderstel byvoorbeeld dat `n aksiepop van 6 sentimeter `n halwe meter van a af is konvergerende lens met `n brandpunt van 20 sentimeter geplaas word. As ons die vergroting, beeld grootte en beeld afstand ons wil bepaal, dan begin ons deur die vergelyking te skryf:
- M = (hi/hO) = -(di/dO)
- Op hierdie stadium weet ons hO (die hoogte van die aksiepop) en dO (die afstand van die aksiepop na die lens.) Ons ken ook die brandpuntsafstand van die lens, wat nie by die vergelyking ingesluit is nie. ons sal nou hi, di en M moet vind.
2. Gebruik die lensvergelyking om d te vindi om te besluit. As jy die afstand van die voorwerp wat jy vergroot vanaf die lens en die brandpuntafstand van die lens weet, is dit maklik om die afstand van die beeld te bepaal deur die lensvergelyking te gebruik. Die lensvergelyking is 1/f = 1/dO + 1/di, waar f = die brandpunt van die lens.
- 1/f = 1/dO + 1/di
- 1/20 = 1/50 + 1/di
- 5/100 - 2/100 = 1/di
- 3/100 = 1/di
- 100/3 = di = 33.3 sentimeter
3. Los op vir hi. weet jy dO en di, dan kan jy die hoogte van die vergrote beeld en die vergroting van die lens vind. Let op die twee gelyke tekens in die vergelyking (M = (hi/hO) = -(di/dO)) — dit beteken dat alle terme gelyk aan mekaar is, dus het ons nou M en hi kan bepaal, in enige volgorde.
- (hi/hO) = -(di/dO)
- (hi/6) = -(33.3/50)
- hi = -(33.3/50) × 6
- hi = -3.996 cm
4. Los op vir M. Jy kan nou die laaste veranderlike oplos met -(di/dO) of met (hi/hO).
- M = (hi/hO)
- M = (-3.996/6) = -0.666
- M = -(di/dO)
- M = -(33.3/50) = -0.666
5. Interpreteer die waarde van M. Sodra jy die vergroting gevind het, kan jy verskillende dinge voorspel oor die beeld wat jy deur die lens sal sien. Hierdie is:
6. Gebruik `n negatiewe brandpunt vir divergerende lense. Selfs al lyk divergerende lense baie anders as konvergerende lense, kan jy hul vergroting bepaal deur dieselfde formules hierbo genoem. Die enigste beduidende uitsondering is dit divergerende lense het `n negatiewe brandpuntsafstand om te hê. In `n soortgelyke probleem soos hierbo aangedui, sal dit die waarde van d beïnvloedi, maak dus seker jy gee aandag daaraan.
- 1/f = 1/dO + 1/di
- 1/-20 = 1/50 + 1/di
- -5/100 - 2/100 = 1/di
- -7/100 = 1/di
- -100/7 = di = -14.29 sentimeter
- (hi/hO) = -(di/dO)
- (hi/6) = -(-14.29/50)
- hi = -(-14.29/50) × 6
- hi = 1.71 sentimeter
- M = (hi/hO)
- M = (1.71/6) = 0.285
Metode 2 van 2: Bepaal die vergroting van veelvuldige lense in `n ry
Twee-lens metode
1. Bepaal die brandpuntsafstand vir beide lense. Wanneer jy te doen het met `n toestel wat twee lense in `n ry gebruik (soos in `n teleskoop of `n deel van `n verkyker), is al wat jy moet weet die brandpunt van beide lense om die finale vergroting van die beeld te kry bepaal. Jy doen dit met die eenvoudige vergelyking M = fO/fe.
- In die vergelyking verwys fO na die brandpunt van die lens en fe na die brandpunt van die oogstuk. Die doelwit is die groot lens aan die einde van die toestel, terwyl die oogstuk die deel is waardeur jy kyk.
2. Gebruik hierdie data in die vergelyking M = fO/fe. Sodra jy die brandpuntsafstand vir albei lense gevind het, word dit maklik om die probleem op te los; jy vind die verhouding deur die brandpunt van die objektief deur dié van die oogstuk te deel. Die antwoord is die vergroting van die toestel.
Gedetailleerde metode
- Gestel ons het byvoorbeeld dieselfde opstelling as in die voorbeeld van Metode 1: `n 6 sentimeter voorwerp op `n afstand van 50 sentimeter vanaf `n konvergerende lens met `n brandpuntsafstand van 20 sentimeter. Nou plaas ons `n tweede konvergerende lens met `n brandpuntsafstand van 5 sentimeter agter die eerste lens (100 sentimeter weg van die aksiepop.) In die volgende stappe sal ons hierdie inligting gebruik om die vergroting van die finale prent te vind.
- Uit ons werk in Metode 1 weet ons dat die eerste lens `n beeld van -3.996 sentimeter hoog, 33.3 sentimeter agter die lens, en met `n vergroting van -0.666.
- In ons voorbeeld is dit 50-33.3 = 16.7 sentimeter vir die tweede, want die beeld 33.3 sentimeter agter die eerste lens. Kom ons gebruik dit, saam met die brandpuntafstand van die nuwe lens, om die beeld van die tweede lens te vind.
- 1/f = 1/dO + 1/di
- 1/5 = 1/16.7 + 1/di
- 0.2 - 0.0599 = 1/di
- 0.14 = 1/di
- di= 7.14 sentimeter
- Nou kan ons hi en bereken M vir die tweede lens:
- (hi/hO) = -(di/dO)
- (hi/-3.996) = -(7.14/16.7)
- hi = -(0,427) × -3.996
- hi = 1.71 sentimeter
- M = (hi/hO)
- M = (1.71/-3.996) = -0,428
- Moenie vergeet dat die volgende lense jou beeld weer kan omkeer nie. Byvoorbeeld, die vergroting wat ons hierbo bereken het (-0,428) dui aan dat die beeld ongeveer 4/10 die grootte van die beeld vanaf die eerste lens is, maar regop, omdat die beeld van die eerste lens omgekeer is.
1. Bepaal die afstand tussen die lense en die voorwerp. As jy twee lense voor `n voorwerp plaas, is dit moontlik om die vergroting van die finale beeld te bepaal, mits jy die verhouding van die afstand van die lense tot die voorwerp, die grootte van die voorwerp en die brandpunt van die voorwerp, albei lense. Alles anders kan jy jou aandag aflei.
2. Bepaal die beeldafstand, hoogte en vergroting vir lens nommer 1. Die eerste deel van enige probleem wat veelvuldige lense behels, is dieselfde as dié wat net een lens behels. Begin met die lens naaste aan die voorwerp, en gebruik die lensvergelyking om die afstand vanaf die beeld te vind; Gebruik nou die vergrotingsvergelyking om die hoogte en vergroting van die beeld te vind.
3. Gebruik die beeld van die eerste as `n voorwerp vir die tweede. Bepaal nou die vergroting, hoogte, ens. vir die tweede lens maklik; gebruik net dieselfde tegnieke as wat vir die eerste lens gebruik is. Net hierdie keer gebruik jy die beeld in plaas van die voorwerp. Onthou dat die beeld gewoonlik op `n ander afstand van die tweede lens sal wees in vergelyking met die afstand tussen die voorwerp en die eerste lens.
4. Gaan so voort met enige bykomende lense. Die standaardbenadering is dieselfde of jy 3, 4 of 100 lense in `n ry vir `n voorwerp plaas. Vir elke lens, beskou die beeld van die vorige lens as die voorwerp en gebruik dan die lensvergelyking en vergrotingsvergelyking om die antwoord te bereken.
Wenke
- Verkykers word gewoonlik deur `n vermenigvuldiging van twee getalle aangedui. Verkykers kan byvoorbeeld as 8x25 of 8x40 gemerk word. Die eerste getal is die vergroting van die verkyker. Die tweede nommer is die skerpte van die beeld.
- Let daarop dat `n vergroting met `n enkele lens, hierdie vergroting `n negatiewe getal is as die afstand na die voorwerp groter is as die brandpunt van die lens. Dit beteken nie dat die voorwerp kleiner sal lyk nie, maar dat die beeld omgekeerd waargeneem sal word.
Artikels oor die onderwerp "Bereken vergroting"
Оцените, пожалуйста статью
Gewilde
