In algemene woorde, A+B = Kom ons voeg die twee vektore A en B by. A = <5, 9, -10> en B = <17, -3, -2>. A + B = <5+17, 9+-3, -10+-2>, of <22, 6, -12>. 
In algemene woorde, A-B = Kom ons trek die twee vektore A en B af. A = <18, 5, 3> en B = <-10, 9, -10>. A - B = <18--10, 5-9, 3--10>, of <28, -4, 13>. 

Let daarop dat die volgorde waarin jy die vektore teken nie belangrik is nie, solank ons aanneem dat jy altyd dieselfde beginpunt gebruik. Vektor A + Vektor B = Vektor B + Vektor A 


Aangesien jy alle vektore volgens skaal geteken het en die hoeke presies gemeet het, kan jy die grootte van die resulterende vektor vind deur die lengte te meet. Jy kan ook die hoek meet wat hierdie resultant maak met `n spesifieke vektor of met die horisontale/vertikale ens. om die rigting te vind. Aangesien jy nie alle vektore volgens skaal geteken het nie, sal jy waarskynlik die grootte van die resultant met behulp van trigonometrie moet bereken. Gebruik die sinus- of cosinusreël hiervoor. Aangesien jy meer as twee vektore byvoeg, is dit nuttig om eers twee daarvan by te voeg, dan hul resultant by die derde vektor te voeg, ensovoorts. Sien die volgende afdeling vir meer inligting. 
Byvoorbeeld, as die vektore wat ons bygevoeg het `n snelheidsvektor in ms voorstel, kan ons die resulterende vektor voorstel as "`n snelheidsvektor van X mev by y relatief tot die horisontale". 

Ons neem byvoorbeeld die vektor van die vorige stap, <-2.12 en 2.12>, en voeg dit by die vektor <5.78 en -9>. In hierdie geval is ons resulterende vektor <-2.12+5.78 en 2.12-9>, of <3,66 en-6,88>. 
Om die grootte van die vektor wie se komponente ons in die vorige stap bepaal het, te vind, <3,66 en -6,88>, ons gebruik die Pythagoras-stelling. Los soos volg op: c=(3.66)+(-6.88) c=13.40+47.33 c=√60.73 = 7,79 
Om die rigting van ons voorbeeldvektor te bepaal, gebruik ons θ=tan(b/a). θ=bruin(-6.88/3.66) θ=bruin(-1.88) θ=-61.99 
Byvoorbeeld, as die voorbeeldvektor `n krag voorstel (in Newton), kan ons dit skryf as "`n krag van 7,79 N aan -61,99 vanaf die horisontale".
Bereken met vektore
Inhoud
Vektore is hoeveelhede wat uit `n grootte en `n rigting bestaan (byvoorbeeld: snelheidsvektor of vektorsnelheid, versnelling en verplasing), in teenstelling met skalare, wat net grootte het (soos spoed, afstand en energie). Terwyl skalare saamgetel kan word deur hul groottes (bv. 5 kJ + 6kJ = 11kJ), is vektore `n bietjie meer ingewikkeld om mee te bereken. Sien Stap 1 hieronder om meer te wete te kom oor maniere om dit te doen.
Trappe
Metode 1 van 3: Optel en aftrek van vektore

1. Druk die afmetings van `n vektor uit deur vektornotasie te gebruik. Omdat vektore `n grootte en `n rigting het, is dit gewoonlik maklik om hulle af te breek in hul x-, y- en/of z-afmetings. Hierdie afmetings word gewoonlik uitgedruk in `n notasie gelykstaande aan die beskrywing van `n punt in `n koördinaatstelsel (bv. Let daarop dat vektore 1, 2 of 3-dimensioneel kan wees. Vektore kan dus `n x-komponent, `n x en y-komponent, of `n x, y ens-komponent hê. Ons voorbeeld hieronder handel oor 3-dimensionele vektore, maar die proses is soortgelyk aan dié van die vlak of `n lyn. Kom ons neem aan ons het twee 3-dimensionele vektore, vektor A en vektor B. Ons kan hierdie vektore in vektornotasie skryf as A =

2. Om twee vektore bymekaar te tel, voeg die komponente by. As die komponente van twee vektore bekend is, dan is dit moontlik om die vektore te bepaal deur hul ooreenstemmende komponente by te voeg. Met ander woorde, voeg die x-komponent van die eerste vektor by die x-komponent van die tweede en doen dieselfde vir y en z. Die antwoorde wat jy kry deur x-, y- en z-komponente van die oorspronklike vektore by te voeg, is die x-, y- en z-komponente van die nuwe vektor.

3. Om twee vektore af te trek, trek jy hul komponente af. Dus dieselfde as met optelling, maar omgekeerd.As die komponente van twee vektore bekend is, is die aftrekking van een vektor van die ander nie meer as om die komponente af te trek nie.
Metode 2 van 3: Optel en aftrek deur die agterste metode te gebruik

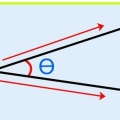
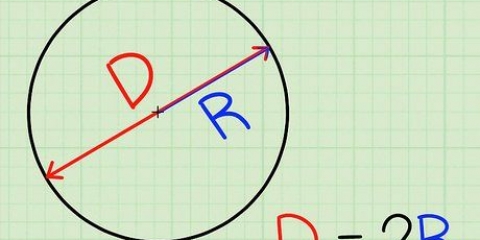
1. Dui vektore met `n pyl aan. Omdat vektore `n grootte en `n rigting het, kan jy hulle met `n pyl aandui. Met ander woorde, hulle het `n "beginpunt" en a "eindpunt", wys in die rigting van die vektor, met die grootte van die vektor wat deur die pyl aangedui word.
- Wanneer jy `n vektor volgens skaal teken, moet jy die hoeke noukeurig meet. Verkeerde hoeke sal lei tot `n verkeerde antwoord met hierdie metode.

2. Teken die pyle in agterste volgorde. Die kop van die pyl word teen die stert van die volgende pyl geplaas. Aangesien jy net twee vektore byvoeg, is dit al wat jy hoef te doen om die resulterende vektor te vind.

3. Om af te trek maak die vektor "negatief". Om vektore met hierdie visuele metode af te trek is relatief maklik. Draai die rigting van die vektor om, maar hou die grootte dieselfde, en voeg dit by met die kop-tot-stert-metode soos gewoonlik. Met ander woorde, om `n vektor af te trek, draai jy die vektor 180 en tel op.

4. As jy meer as twee vektore wil byvoeg of aftrek, koppel dan al daardie vektore een na die ander deur die agterste metode te gebruik. Die volgorde maak nie saak nie. Jy kan dit vir enige aantal vektore gebruik.
5. Teken `n nuwe vektor vanaf die stert van die eerste vektor tot by die kop van die laaste. Of jy nou met 2 of 100 vektore werk, die vektor wat strek vanaf die beginpunt (die stert van jou eerste vektor) tot by die eindpunt van die bygevoegde vektore (die kop van jou laaste vektor) is die gevolglike vektor, of die som van alle vektore. Let daarop dat hierdie vektor gelyk is aan die vektor wat verkry word deur die x-, y- en/of z-komponente van alle vektore by te tel.


6. Vertoon die resulterende vektor volgens grootte en rigting. Vektore word bepaal deur hul lengte en rigting. Soos hierbo genoem, as jy aanvaar dat jy die vektore akkuraat geteken het, is die grootte van die vektor gelyk aan sy lengte en rigting, en sy hoek is relatief tot die vertikale, horisontale, ens. Gebruik die eenhede van die vektore wat jy saamgevoeg het om die eenhede vir die grootte van die resulterende vektor te kies.
Metode 3 van 3: Optel en aftrek van vektore deur die komponente te bepaal

1. Gebruik trigonometrie om die vektor se komponente te vind. Jy benodig die grootte en rigting relatief tot die horisontale of vertikale, en jy moet `n bietjie werkende kennis van trigonometrie hê. Gestel ons het `n 2-D vektor. Eerstens maak jy die vektore die skuinssy van `n reghoekige driehoek, met die ander twee sye parallel aan die x- en y-asse. Jy kan aan hierdie twee kante dink as kop-tot-stert vektore wat, wanneer dit saamgevoeg word, die oorspronklike vektor lewer.
- Die lengtes van die twee sye is gelyk aan die groottes van die x- en y-komponente van jou vektor en kan met behulp van trigonometrie bereken word. As x die grootte van die vektor is, dan is die sy aangrensend aan die hoek van die vektor (relatief tot die horisontale, vertikale, ens.) gelyk aan xcos(θ), terwyl die teenoorgestelde gelyk is aan xsin(θ).
- Dit is ook belangrik om die oriëntasie van jou komponente in ag te neem. As die komponent in die negatiewe rigting van een van die asse wys, kry dit `n minusteken. Byvoorbeeld, as `n komponent na links of na onder in die vliegtuig wys, kry dit `n minusteken.
- Byvoorbeeld, kom ons sê ons het `n vektor van grootte 3 en `n rigting 135 relatief tot die horisontale. Met hierdie inligting kan ons bepaal dat die x-komponent gelyk is aan 3cos(135) = -2.12 en die y-komponent is 3sin(135) = 2.12

2. Tel die ooreenstemmende komponente van twee of meer vektore bymekaar. Wanneer jy die komponente van al die vektore gevind het, tel eenvoudig die groottes bymekaar om die komponente van jou resulterende vektor te vind. Tel eers die groottes van die horisontale komponente by (parallel aan die x-as). Voeg dan die groottes van die vertikale komponente by (parallel aan die y-as). As `n komponent `n minusteken (-) voor dit het, word die grootte daarvan afgetrek. Die antwoorde wat jy kry is die komponente van jou resulterende vektor.

3. Bereken die grootte van die resulterende vektor deur die Pythagoras-stelling te gebruik. Met hierdie stelling, c=a+b, kan jy die lengte van die sye van reghoekige driehoeke vind?. Aangesien die driehoek wat deur die resulterende vektor en sy komponente gevorm word `n reghoekige driehoek is, kan ons hierdie stelling gebruik om die vektor se lengte en dus sy grootte te vind. Van c as die grootte van die resulterende vektor wat jy probeer vind, sê a in as die grootte van die x-komponent en b as die grootte van die y-komponent. Los op met algebra.

4. Bereken die rigting van die resultant met die raaklyn. Laastens bepaal ons die rigting van die resulterende vektor. Gebruik die formule θ=bruin(b/a), waar θ die hoek is wat die resultant met die x-as vanaf die horisontale maak, waar b die grootte van die y-komponent is en a die grootte van die x-komponent is.

5. Vertoon die resulterende vektor volgens grootte en rigting. Soos hierbo aangedui, word vektore gedefinieer deur hul grootte en rigting. Maak seker jy gebruik die korrekte eenhede vir die vektorgrootte.
Wenke
- Vektore moet nie met groottes verwar word nie.
- Jy kan die grootte van `n vektor in die ruimte vind deur die formule a=b+c+d om te gebruik, waar a is die grootte van die vektor en b, c en d die komponente in elke rigting.
- Vektore voorgestel as xi + yj + Zk kan opgetel of afgetrek word deur eenvoudig die koëffisiënte van die drie vektore op te tel of af te trek. Die antwoord is dan ook in die vorm i, j, k.
- Kolomvektore kan opgetel en afgetrek word deur die waardes in elke ry op te tel of af te trek.
Artikels oor die onderwerp "Bereken met vektore"
Оцените, пожалуйста статью
Gewilde