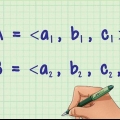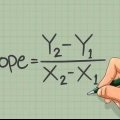Vind die hoek tussen twee vektore

Inhoud

Trappe
Wenke

Wiskundiges en fisici moet dikwels die hoek tussen twee gegewe vektore vind. Alhoewel dit maklik is om die hoek tussen twee vektore in dieselfde vlak te vind deur grafieke te teken, kan dit `n bietjie moeiliker wees in ruimte of in drie dimensies. Hierdie artikel verduidelik die metode om te gebruik om die hoek tussen twee vektore in die vlak of in die ruimte te vind.

Trappe

Metode 1 van 4: Bepaal die vektore

1. Bepaal die vektore wat jy nodig het om die hoek te vind. Neem die twee vektore AAN en OQ wat by punt O sny, en bereken die hoek MOQ. Jy moet die vektore gebruik AAN en OQ gebruik, moenie MO of QO. In die geval dat MO bekend is, vermenigvuldig dit met -1 om te kry AAN om te kry.

Metode 2 van 4: Vind die skalêre produk

Vind die skalaarproduk (of puntproduk) van die twee vektore. As jy nie weet hoe om die skalêre produk van twee vektore te bereken nie, lees verder:

1. Bepaal die komponente van die vektor in elke rigting. Wanneer die vektore in `n tabel gelys word, verteenwoordig die eerste ry gewoonlik die x-as, die tweede ry verteenwoordig die y-as en die derde verteenwoordig die z-as. As die vektor in die vorm x geskryf isi + yj + Zk, stel dan die koëffisiënte van ek, jo, en k die grootte van die komponente langs die x-, y- en z-asse (ek, jo, en k is die vektore langs die x-, y- en z-asse).

2. Vermenigvuldig die komponente van beide vektore langs die x-as. Vermenigvuldig dan die komponente van beide vektore langs die y-as en doen dieselfde vir die komponente langs die z-as.

3. Voeg die drie produkte saam. Dit is die skalaarproduk van beide vektore. Die skalêre produk, of "interne produk", van twee vektore is `n baie nuttige getal in meetkunde en fisika. Op die oomblik gebruik ons hierdie produk net as `n hulpmiddel om die hoek tussen twee vektore te bereken. In `n tweedimensionele vektor is die komponent langs die z-as nul, dus kan die skalêre produk gevind word deur slegs die komponente langs die x- en y-as te oorweeg.

Metode 3 van 4: Bereken die grootte

1. Bereken die grootte van die twee vektore. Bereken die grootte van die twee vektore deur die formule te gebruik a=b+c+d, waardeur a is die grootte van die vektor, en b,c, en d die grootte van die komponente in die drie verskillende rigtings. In die plat vliegtuig d gelyk aan nul wees.

Metode 4 van 4: = Vind die hoek

1. Gebruik die waardes wat hierbo bereken is in hierdie formule: cosθ = a.b / |a||b|

2. Lei die inverse cosinus hieruit af.

3. Klaar.

Wenke

Jy kan hierdie metode gebruik om die hoek in 3D- of x-y-z-grafieke te bereken deur die sye as vektore te beskou en die vektor as vrye vektore te behandel.