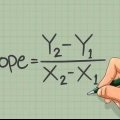Hoe om akkuraatheid te bepaal

Inhoud

Trappe
Wenke

Akkuraatheid beteken dat `n meting met `n spesifieke instrument of instrument soortgelyke resultate lewer elke keer as dit gebruik word. Byvoorbeeld, as jy vyf keer in `n ry op `n skaal trap, moet `n presiese skaal jou elke keer dieselfde gewig wys. In wiskunde en wetenskap is die berekening van akkuraatheid noodsaaklik om te bepaal of jou instrumente en metings goed genoeg is om goeie data te kry. Jy kan die akkuraatheid van elke datastel voorstel deur die reeks van die waardes, die gemiddelde afwyking of die standaardafwyking te gebruik.

Trappe

Metode 1 van 4: Bereken die reeks

1. Bepaal die hoogste gemete waarde. Dit help om jou data in numeriese volgorde te begin sorteer, van laagste na hoogste. Dit sal verseker dat jy nie enige van die waardes oorslaan nie. Kies dan die waarde aan die einde van die lys.

Sê byvoorbeeld jy toets die akkuraatheid van `n skaal en sien vyf lesings: 11, 13, 12, 14, 12. Gesorteer word hierdie waardes getoon as 11, 12, 12, 13, 14. Die hoogste waarde is 14.

Prent getiteld Bereken akkuraatheid Stap 2

2. Bepaal die laagste gemete waarde. Sodra jou data gesorteer is, is dit so eenvoudig om die laagste waarde te vind as om aan die begin van die lys te kyk.

Binne die meetdata van die skaal is die laagste waarde 11.

3. Trek die laagste waarde van die hoogste af. Die omvang van `n stel data is die verskil tussen die hoogste en laagste lesings. Trek net van mekaar af. Algebraïes word die reeks uitgedruk as:

reeks = X (m a X) - X (m i n)

${text{Reikwydte}}=x(maks)-x(min)$

Die omvang van die voorbeelddata is:

reeks = X (m a X) - X (m i n) = 14 - 11 = 3

${text{Reikwydte}}=x(maks)-x(min)=14-11=3$

Prent getiteld Bereken akkuraatheid Stap 4

4. Vertoon die reeks as die akkuraatheid. Wanneer data gerapporteer word, is dit belangrik dat lesers weet wat jy gemeet het. Omdat akkuraatheid in verskillende maatstawwe voorkom, moet jy spesifiseer wat jy wil rapporteer. Vir hierdie data noem jy: gemiddelde = 12.4, reeks = 3. Of eenvoudig: gemiddeld = 12,4 ±3.

Die gemiddelde is nie noodwendig deel van die berekening van omvang of akkuraatheid nie, maar is gewoonlik die eerste berekening om die gemete waarde aan te gee. Die gemiddelde word verkry deur die som van die gemete waardes te deel deur die aantal items in die groep. Die gemiddelde van hierdie datareeks is (11 + 13 + 12 + 14 + 12) / 5 = 12.4.

Metode 2 van 4: Berekening van gemiddelde afwyking

Prent getiteld Bereken akkuraatheid Stap 5

1. Bepaal eers die gemiddelde van die data. Die gemiddelde afwyking is `n meer gedetailleerde maatstaf van die akkuraatheid van `n groep metings of waardes van `n eksperiment. Die eerste stap om die gemiddelde afwyking te vind, is om die gemiddelde van die gemete waardes te bereken. Die gemiddelde is die som van die waardes gedeel deur die aantal metings.

In hierdie voorbeeld gebruik ons dieselfde voorbeelddata as voorheen. Aanvaar dat vyf metings geneem is, 11, 12, 13, 14 en 12. Die gemiddelde van hierdie waardes is (11 + 13 + 12 + 14 + 12) / 5 = 12.4.

Prent getiteld Bereken akkuraatheid Stap 6

2. Bereken die absolute afwyking van elke waarde van die gemiddelde. Vir hierdie berekening van akkuraatheid moet jy bepaal hoe naby elke waarde aan die gemiddelde is. Om dit te doen, trek die gemiddelde van elke getal af. Vir hierdie meting maak dit nie saak of die waarde bo of onder die gemiddelde is nie. Trek die getalle af en gebruik net die positiewe waarde van die resultaat. Dit staan ook bekend as die `absolute waarde`.

Algebraïes word die absolute waarde voorgestel deur twee vertikale stawe om die berekening te plaas. Soos volg:

Absolute afwyking = | X - μ |

${text{Absolute afwyking}}=|x-mu |$

Hierdie berekening stel

X

$X$ vir elk van die eksperimentele waardes en

μ

$mu$ vir die berekende gemiddelde.

Wat die waardes van die monsterdatareeks betref, is die absolute afwykings:

| 12 - 12, 4 | = 0, 4

$|12-12.4|=0.4$

| 11 - 12, 4 | = 1, 4

$|11-12.4|=1.4$

| 14 - 12, 4 | = 1, 6

$|14-12.4|=1.6$

| 13 - 12, 4 | = 0, 6

$|13-12.4|=0.6$

| 12 - 12, 4 | = 0, 4

$|12-12.4|=0.4$

Prent getiteld Bereken akkuraatheid Stap 7

3. Bepaal die gemiddelde afwyking. Gebruik die absolute afwykings en vind hul gemiddelde. Soos met die oorspronklike stel data, voeg jy die waardes bymekaar en deel die som deur die aantal waardes. Dit word algebraïes voorgestel as:

Gemiddelde afwyking = Σ | X - μ | n

${text{Gemiddelde Afwyking}}={frac{Sigma |x-mu |}{n}}$

Wat hierdie voorbeelddata betref, gaan die berekening soos volg uit:

Gemiddelde afwyking = 0, 4 + 1, 4 + 1, 6 + 0, 6 + 0, 4 5

${text{Gemiddelde afwyking}}={frac{0.4+1.4+1.6+0.6+0.4}{5}}$

Gemiddelde afwyking = 4, 4 5

${text{Gemiddelde afwyking}}={frac{4,4}{5}}$

Gemiddelde afwyking = 0, 88

${text{Gemiddelde afwyking}}=0.88$

Prent getiteld Bereken akkuraatheid Stap 8

4. Noem die resultaat van die akkuraatheid. Hierdie resultaat kan gerapporteer word as die gemiddelde, plus of minus die gemiddelde afwyking. Vir hierdie steekproefdatastel lyk dit soos 12.4 ±0.88. Let daarop dat om die akkuraatheid as die gemiddelde afwyking te noem, die meting baie meer akkuraat laat lyk as met die reeks.

Metode 3 van 4: Bereken die standaardafwyking

Prent getiteld Bereken akkuraatheid Stap 9

1. Gebruik die korrekte formule vir die standaardafwyking. Vir enige datastelgrootte is die standaardafwyking `n betroubare statistiek om akkuraatheid te vertoon. Daar is twee formules vir die berekening van die standaardafwyking, met `n baie klein verskil tussen hulle. Jy gebruik een formule as jou maatstawwe `n hele populasie dek. Die tweede formule word gebruik as die gemete data slegs `n steekproef van die populasie is.

Jou data verteenwoordig `n hele populasie as jy alle moontlike maatstawwe van alle moontlike vakke versamel het. Byvoorbeeld, as jy mense met `n baie seldsame siekte toets, en jy is vol vertroue dat jy almal met hierdie siekte getoets het, sluit dit die hele bevolking in. Die formule vir die standaardafwyking in hierdie geval is:

$Σ = \sqrt{} Σ (X - μ) 2 n$ $sigma ={sqrt{{frac{Sigma (x-mu )^{2}}{n}}}}$

`n Steekproef is `n groep data kleiner as `n hele populasie. Jy sal gewoonlik hierdie een die meeste gebruik. Die standaardafwykingsformule vir `n steekproef is:

Σ = \sqrt{} Σ (X - μ) 2 n - 1

$sigma ={sqrt{{frac{Sigma (x-mu)^{2}}{n-1}}}}$

Let daarop dat die enigste verskil die noemer van die breuk is. Vir `n volle bevolking, deel deur

n

$n$ . As jy `n voorbeeld het, deel asseblief

n - 1

$n-1$ .

2. Vind die gemiddelde van die datawaardes. Soos met die berekening van die gemiddelde afwyking, begin jy deur die gemiddelde van die datawaardes te bepaal.

Deur dieselfde stel lesings te gebruik as hierbo genoem, is die gemiddelde 12,4.

Prent getiteld Bereken akkuraatheid Stap 11

3. Vind die vierkant van elke variant. Trek die datawaarde van die gemiddelde af vir elke datapunt en kwadraat die resultaat. Aangesien jy hierdie variasies kwadrateer, maak dit nie saak of die verskil positief of negatief is nie. Die vierkant van die verskil is altyd positief.

Vir die vyf datawaardes in hierdie voorbeeld gaan hierdie berekeninge soos volg:

(12 - 12, 4) 2 = (- 0, 4)^{2} = 0, 16

$(12-12.4)^{2}=(-0.4)^{2}=0.16$

(11 - 12, 4) 2 = (- 1, 4)^{2} = 1, 96

$(11-12.4)^{2}=(-1.4)^{2}=1.96$

(14 - 12, 4) 2 = 1, 6^{2} = 2, 56

$(14-12.4)^{2}=1.6^{2}=2.56$

(13 - 12, 4) 2 = 0, 6^{2} = 0, 36

$(13-12.4)^{2}=0.6^{2}=0.36$

(12 - 12, 4) 2 = (- 0, 4)^{2} = 0, 16

$(12-12.4)^{2}=(-0.4)^{2}=0.16$

Prent getiteld Bereken akkuraatheid Stap 12

4. Bereken die som van die kwadraatverskille. Die teller van die breuk in die standaardafwyking is die som van die kwadraatverskille tussen die waardes en die gemiddelde. Jy kan hierdie bedrag bepaal deur die getalle van die vorige berekening bymekaar te tel.

Vir die voorbeelddatastel is dit:

0, 16 + 1, 96 + 2, 56 + 0, 36 + 0, 16 = 5, 2

$0,16+1,96+2,56+0,36+0,16=5,2$

5. Verdeel volgens datagrootte. Dit is die enigste stap wat verskil in `n populasieberekening in vergelyking met `n steekproef. Vir `n volledige bevolking, deel jy deur

n

$n$ (die aantal waardes). In `n steekproef deel jy deur

n - 1

$n-1$ .

Die volgende voorbeeld het slegs vyf mates en is dus slegs `n steekproef. Dus vir die vyf waardes wat gebruik word, deel deur (5 - 1) of 4. Die resultaat is

5, 2 / 4 = 1, 3

$5.2/4=1.3$ .

6. Vind die vierkantswortel van die resultaat. Op hierdie punt verteenwoordig die berekening wat die variansie van die datastel genoem word. Die standaardafwyking is die vierkantswortel van die variansie. Gebruik `n sakrekenaar om die vierkantswortel te vind, en daarmee saam die standaardafwyking.

Σ = \sqrt{1.3} = 1, 14

$sigma ={sqrt{1.3}}=1,14$

7. Wys jou resultaat. Deur hierdie berekening te gebruik, kan die akkuraatheid van die skaal aangedui word deur die gemiddelde plus of minus die standaardafwyking te noem. Vir hierdie data word dit 12,4 ±1,14.

Die standaardafwyking is miskien die mees algemene maatstaf van akkuraatheid. Vir duidelikheid is dit egter steeds `n goeie idee om `n voetnoot of hakies te gebruik om aan te dui dat die presisiewaarde die standaardafwyking verteenwoordig.

Metode 4 van 4: Besluit hoe om akkuraatheid te stel

1. Gebruik die woord akkuraatheid korrek. Akkuraatheid is `n term wat gebruik word om die herhaalbaarheid van metings aan te dui. As jy `n groep data insamel, hetsy deur meting of deur `n spesifieke eksperiment, beskryf die akkuraatheid hoe na aan mekaar die resultate van elke meting of eksperiment sal wees.

Akkuraatheid is nie dieselfde as akkuraatheid nie. Akkuraatheid meet hoe naby eksperimentele waardes aan die werklike of teoretiese waarde is, terwyl akkuraatheid meet hoe naby die gemete waardes aan mekaar is.
Data kan akkuraat maar nie akkuraat of akkuraat maar nie akkuraat wees nie. Akkurate lesings kan naby aan die teiken wees, maar dalk nie naby mekaar nie. Akkurate lesings is naby aan mekaar of dit naby teikenwaardes is of nie.

2. Kies die beste graad van akkuraatheid. Die woord `akkuraatheid` het nie `n enkele betekenis nie. Dit is moontlik om akkuraatheid met verskeie verskillende metings te vertoon. Jy sal moet besluit watter een die beste is.

Reeks. Vir klein datastelle met ongeveer tien of minder metings, is die reeks waardes `n goeie maatstaf van akkuraatheid. Dit is veral waar as die waardes redelik nou saam gegroepeer is. As jy vind dat een of twee waardes ver van die ander waardes is, moet jy waarskynlik `n ander berekening gebruik.

Gemiddelde afwyking. Die gemiddelde afwyking is `n meer akkurate maatstaf van die akkuraatheid van `n klein stel datawaardes.

standaard afwyking. Die standaardafwyking is miskien die mees erkende maatstaf van akkuraatheid. Standaardafwyking kan gebruik word om die akkuraatheid van die metings vir `n hele populasie of `n steekproef van die populasie te bereken.

3. Gee `n duidelike voorstelling van jou resultate. Baie dikwels sal navorsers data rapporteer deur die gemiddelde van die gemete waarde te gee, gevolg deur die graad van akkuraatheid. Die akkuraatheid word getoon met die `±`-simbool. Dit gee `n aanduiding van akkuraatheid, maar dit verduidelik nie duidelik aan die leser of die getal na die `±`-simbool `n reeks, standaardafwyking of `n ander meting is nie. Om dit duidelik te stel, moet jy definieer watter vlak van akkuraatheid jy gebruik het, hetsy in `n voetnoot of as `n opmerking tussen hakies.

Vir `n gegewe datareeks kan die resultaat as 12.4 ±3 vertoon word. `n Meer beskrywende manier om dieselfde data te stel sal egter die volgende wees: `Gemiddeld = 12.4, Omvang = 3.`

Wenke

As een van die waardes in die steekproef baie hoër of laer is as die res van jou waardes, moenie hierdie waarde van jou berekeninge uitsluit nie. Selfs al was dit `n fout, bly dit data en moet dit vir korrekte berekening gebruik word.
Slegs vyf waardes is in hierdie artikel gebruik vir wiskundige eenvoud. In `n werklike eksperiment moet jy meer as vyf maatstawwe gebruik vir `n meer akkurate berekening. Hoe meer monsters jy hardloop, hoe meer akkuraat.