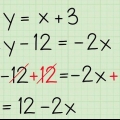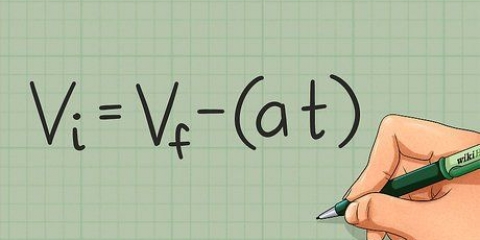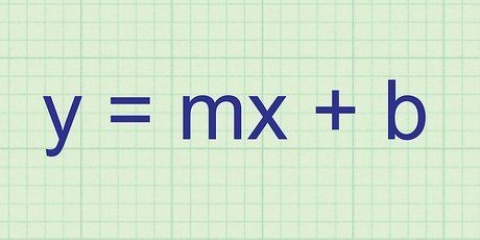Hoe om te bepaal of twee lyne parallel is

Inhoud

Trappe

Parallelle lyne is twee lyne in `n vliegtuig wat nooit sal sny nie (wat beteken dat hulle vir ewig sal aanhou sonder om ooit aan te raak). `n Belangrike kenmerk van parallelle lyne is dat hulle identiese hellings het. Die helling van `n lyn word gedefinieer as die styging (verandering in y-koördinate) oor die daling (verandering in x-koördinate) van `n lyn, met ander woorde hoe steil die lyn is. Parallelle lyne word dikwels voorgestel deur twee vertikale lyne (ll). Byvoorbeeld, AB11CD dui aan dat lyn AB parallel aan CD is.

Trappe

Metode 1 van 3: Vergelyk die helling van elke lyn

Prent getiteld Bepaal of twee lyne parallel is Stap 1

1. Vind die formule vir die helling. Die helling (helling) van `n lyn word gedefinieer deur (Y₂ - Y₁)/(X₂ - X₁) waar X en Y die horisontale en vertikale koördinate van punte op die lyn is. Jy moet twee punte op die lyn bepaal om hierdie formule te bereken. Die punt nader aan die onderkant van die lyn is (X₁, Y₁) en die punt hoër op die lyn, bokant die eerste punt, is (X₂, Y₂).

Hierdie formule kan herformuleer word as die toename oor die afstand. Dit is die vertikale verandering in vergelyking met die horisontale verandering, of die steilheid van die lyn.
As `n lyn na regs en opwaarts wys, sal dit `n positiewe helling hê.
As die lyn na regs en af wys, sal dit `n negatiewe helling hê.

Prent getiteld Bepaal of twee lyne parallel is Stap 2

2. Identifiseer die X- en Y-koördinate van twee punte op elke lyn. `n Punt op `n lyn word gegee deur sy koördinaat (X, Y) waar X die ligging op die horisontale as is en Y die ligging op die vertikale as is. Om die helling te bereken, moet jy twee punte op elk van die betrokke lyne bepaal.

Punte is maklik om te bepaal as jy `n lyn op grafiekpapier getrek het.

Om `n punt te bepaal, trek `n stippellyn op vanaf die horisontale as totdat dit die lyn sny. Die posisie waar jy die lyn op die horisontale as begin het, is die x-koördinaat, terwyl die y-koördinaat is waar die stippellyn die lyn op die vertikale as sny.

Byvoorbeeld: lyn l het die punte (1, 5) en (-2, 4) terwyl lyn r het die punte (3, 3) en (1, -4).

Prent getiteld Bepaal of twee lyne parallel is Stap 3

3. Verwerk die punte vir elke lyn in die hellingsformule. Om die helling te bereken, voer die getalle in, trek af en deel. Maak seker dat jy die koördinate in die korrekte x- en y-waarde in die formule invoeg.

Na die helling van die lyn l om te bereken: helling = (5 - (-4))/(1 - (-2))

Trek af: helling = 9/3

Verdeel: helling = 3

Die helling van die lyn r = (3 - (-4))/(3 - 1) = 7/2

Prent getiteld Bepaal of twee lyne parallel is Stap 4

4. Vergelyk die hellings van elke lyn. Onthou dat twee lyne net parallel is as hulle dieselfde hellings het. Lyne kan ewewydig op papier voorkom en selfs baie naby aan parallel wees, maar as hul hellings nie presies gelyk is nie, is hulle nie ewewydig nie.

In hierdie voorbeeld is 3 nie gelyk aan 7/2 nie, so hierdie twee lyne is nie parallel nie.

Metode 2 van 3: Gebruik die helling- en kruisingsformule

Prent getiteld Bepaal of twee lyne parallel is Stap 5

1. Vind die formule vir helling en snypunt van `n lyn. Die hellingsformule, die vergelyking van `n reguit lyn. is y = mx + b, waar m die helling is, b die snypunt met die y-as is, en x en y is veranderlikes wat koördinate op die lyn verteenwoordig -- gewoonlik sien jy hulle as x en y in die vergelyking. In hierdie vorm kan jy maklik die helling van die lyn bepaal as die veranderlike `m`.

`n Voorbeeld: herskryf 4y - 12x = 20 en y = 3x -1. Die vergelyking 4y - 12x = 20 moet met algebra herskryf word terwyl y = 3x -1 reeds die vorm van die hellingsformule het en nie herskryf hoef te word nie.

Prent getiteld Bepaal of twee lyne parallel is Stap 6

2. Herskryf die formule van die lyn as hellingsformule. Dikwels sal die formule van die lyn wat jy kry nie in die vorm van `n skuins vlak wees nie. Dit verg net `n bietjie wiskunde en veranderlike herrangskikking om dit in die hellingformulevorm te kry.

Byvoorbeeld: Herskryf die reël 4y-12x=20 as hellingsformule.

Tel 12x by albei kante van die vergelyking: 4y - 12x + 12x = 20 + 12x

Deel elke kant deur 4 om y te isoleer: 4y/4 = 12x/4 +20/4

Hellingsformule: y = 3x + 5

Prent getiteld Bepaal of twee lyne parallel is Stap 7

3. Vergelyk die hellings van elke lyn. Onthou dat as twee lyne parallel aan mekaar is, hulle presies dieselfde helling sal hê. Deur die vergelyking y = mx + b te gebruik, waar m die helling van die lyn is, kan jy die hellings van twee lyne bepaal en vergelyk.

In ons voorbeeld het die eerste lyn `n vergelyking van y = 3x + 5, dus die helling is 3. Die ander lyn het `n vergelyking van y = 3x - 1 wat ook `n helling van 3 het. Aangesien die hellings identies is, is hierdie twee lyne parallel.

Let daarop dat as hierdie vergelykings dieselfde snypunt met die y-as het, hulle dieselfde lyn sal wees in plaas van parallel.

Metode 3 van 3: Bepaling van `n parallelle lyn met die punt-helling-vergelyking

Prent getiteld Bepaal of twee lyne parallel is Stap 8

1. Definieer die punt-helling vergelyking. Met die punt-helling vergelyking kan jy die vergelyking van `n lyn skryf as jy die helling ken en `n (x, y) koördinaat het. Jy gebruik hierdie formule as jy `n tweede parallelle lyn op `n reeds gegewe lyn met `n sekere helling wil definieer. Die formule is y – y₁= m(x – x₁) waar m die helling van die lyn is, x₁ die x-koördinaat van `n gegewe punt op die lyn en y₁ die y-koördinaat van daardie punt. Soos in die hellingsformule, is x en y veranderlikes wat koördinate op die lyn verteenwoordig -- gewoonlik sal hulle as x en y in die vergelyking bly.

Die volgende stappe werk hierdie voorbeeld uit: Skryf die vergelyking van `n lyn parallel aan die lyn y = -4x + 3 wat deur punt (1, -2) gaan.

Prent getiteld Bepaal of twee lyne parallel is Stap 9

2. Vind die helling van die eerste lyn. Wanneer jy die vergelyking van `n nuwe lyn skryf, moet jy eers die helling van die lyn bepaal waaraan jou lyn parallel moet wees. Maak seker dat die vergelyking van die oorspronklike lyn `n hellingsformule is sodat jy dadelik die helling (m) ken.

Die lyn wat ons parallel wil maak is y = -4x + 3. In hierdie vergelyking verteenwoordig -4 die veranderlike m en dus die helling van die lyn.

Prent getiteld Bepaal of twee lyne parallel is Stap 10

3. Identifiseer `n punt op die nuwe lyn. Hierdie vergelyking werk net as jy `n koördinaat het wat deur die nuwe lyn gaan. Maak seker dat jy nie `n koördinaat kies wat op die oorspronklike lyn is nie. As jou finale vergelykings dieselfde y-afsnit het, is hulle nie parallel nie, maar dieselfde lyn.

In ons voorbeeld gebruik ons die koördinaat (1, -2).

Prent getiteld Bepaal of twee lyne parallel is Stap 11

4. Skryf die vergelyking van die nuwe lyn in die punt-helling vorm. Onthou die formule is: y – y₁= m(x – x₁). Voer die helling en koördinate van jou punt in om die vergelyking van jou nuwe lyn parallel met die eerste te maak.

Deur ons voorbeeld met helling (m) -4 en (x, y) koördinaat (1, -2) te gebruik, word dit: y – (-2) = -4(x – 1)

Prent getiteld Bepaal of twee lyne parallel is Stap 12

5. Vereenvoudig die vergelyking. Nadat jy die getalle ingevul het, kan die vergelyking na die meer algemene hellingsformule vereenvoudig word. Die lyn van hierdie vergelyking, wanneer dit in `n koördinaatstelsel getrek word, is parallel aan die gegewe vergelyking.

Byvoorbeeld: y - (-2) = -4(x - 1)

Twee negatiewe maak `n positief: y + 2 = -4(x -1)

Gebruik die verspreidingseienskap om -4(x -1) te bereken: y + 2 = -4x + 4.

Trek -2 van beide kante af: y + 2 - 2 = -4x + 4 - 2

Die vereenvoudigde vergelyking: y = -4x + 2