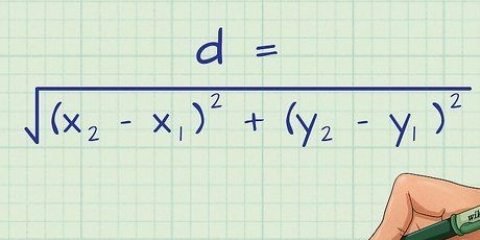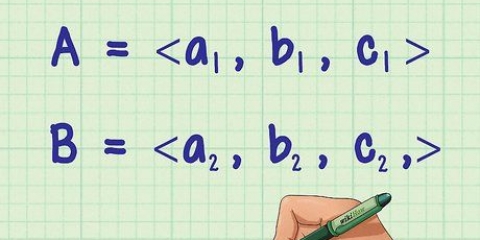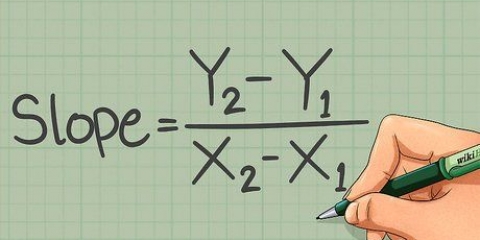Hoe om die afstand tussen twee punte te bereken: 6 stappe (met prente)

Inhoud

Trappe
Wenke

Dink aan die afstand tussen enige twee punte as `n lyn. Die lengte van hierdie lyn kan gevind word deur die afstandformule te gebruik: $\sqrt{(} (X_{2} - X_{1})^{2} + (y_{2} - y_{1})^{2})$ ${sqrt(}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})$ .

Trappe

Prent getiteld Vind die afstand tussen twee punte Stap 2

1. Neem die koördinate van twee punte waartussen jy die afstand wil vind. Noem een punt 1 (x1,y1) en die ander punt 2 (x2,y2). Dit maak nie saak vanaf watter punt jy begin nie, solank jy die etikette (1 en 2) konsekwent deur die hele probleem aanbring.

x1 is die horisontale koördinaat (langs die x-as) van punt 1, en x2 is die horisontale koördinaat van punt 2. y1 is die vertikale koördinaat (langs die y-as) van punt 1, en y2 is die vertikale koördinaat van punt 2.
Nee, byvoorbeeld die punte (3.2) en (7.8). As (3.2) gelyk is aan (x1,y1), dan is (7.8) gelyk aan (x2,y2).

Prent getiteld Vind die afstand tussen twee punte Stap 1

2. Gebruik die afstandsformule. Hierdie formule bepaal die lengte van `n reguit lyn tussen twee punte: punt 1 en punt 2. Die lineêre afstand is die vierkantswortel van die vierkant van die horisontale afstand, plus die vierkant van die vertikale afstand tussen twee punte. Eenvoudig gestel, dit is die vierkantswortel van:

(X 2 - X_{1})^{2} + (y_{2} - y_{1})^{2}

$(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$

Prent getiteld Vind die afstand tussen twee punte Stap 3

3. Bepaal die horisontale en vertikale afstand tussen die punte. Bereken eers y2 - y1 om die vertikale afstand te vind. Bereken dan x2 - x1 om die horisontale afstand te vind. Moenie bekommerd wees as die aftrekking negatiewe getalle produseer nie. Die volgende stap is om hierdie waardes te vier (wat altyd `n positiewe heelgetal tot gevolg het).

Bepaal die afstand langs die y-as. Vir die voorbeeldpunte (3.2) en (7.8), waar punt 1 (3.2) en punt 2 (7.8) is, word dit: (y2 - y1) = 8 - 2 = 6. Dit beteken dat die afstand op die y-as tussen hierdie twee punte ses lengte-eenhede is.

Bepaal die afstand langs die x-as. Vir dieselfde monsterpunte (3.2) en (7.8): (x2 - x1) = 7 - 3 = 4. Dit beteken dat daar vier lengte-eenhede is wat die twee punte op die x-as skei.

Prent getiteld Vind die afstand tussen twee punte Stap 4

4. Vierkant beide waardes. Dit beteken dat jy die afstand van die x-as kwadraat (x2 - x1), en jy die afstand van die y-as kwadraat (y2 - y1).

62 = 36

$6^{2}=36$

42 = 16

$4^{2}=16$

Prent getiteld Vind die afstand tussen twee punte Stap 5

5. Voeg die blokkies bymekaar. Dit sal jou die vierkant van die diagonale, lineêre afstand tussen jou twee punte gee. In die voorbeeld van punte (3.2) en (7.8) is die vierkant van (7 - 3) 16, en die vierkant van (8 - 2) is 36. 36 + 16 = 52.

Prent getiteld Vind die afstand tussen twee punte Stap 6

6. Neem die vierkantswortel van die vergelyking. Dit is die laaste stap in die vergelyking. Die lineêre afstand tussen die twee punte is die vierkantswortel van die som van die vierkante van die afstand op die x-as en die afstand op die y-as.

Gaan voort met die voorbeeld, die afstand tussen (3.2) en (7.8) is die vierkantswortel van 52, of ongeveer 7.21.

Wenke

Dit maak nie saak of jy `n negatiewe getal kry nadat jy y2 - y1 of x2 - x1 afgetrek het nie. Omdat die verskil kwadraat is kry jy altyd `n positiewe afstand in jou antwoord.