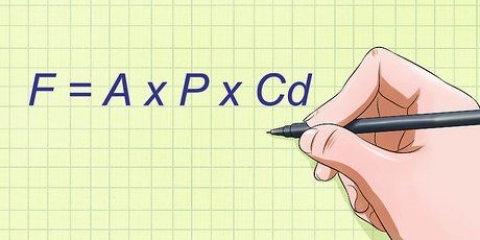Die x-as is die horisontale as; die y-as is die vertikale as. Die koördinate van `n punt word geskryf as  .
. Byvoorbeeld, `n lynsegment kan `n eindpunt hê by  en nog een aan
en nog een aan  .
. 
Byvoorbeeld, met die punte  en
en  , jou formule sal soos volg lyk:
, jou formule sal soos volg lyk: 


Byvoorbeeld:



Byvoorbeeld:



Aangesien jy die vierkantswortel bepaal, moet jy dalk jou antwoord afrond. Aangesien jy vanaf `n koördinaatstelsel werk, sal jou antwoord in die algemeen "eenhede" wees en nie in sentimeters, meters of enige ander eenheid nie. Byvoorbeeld:

 eenhede.
eenhede.
Bereken die lengte van 'n lyn deur die afstandformule te gebruik
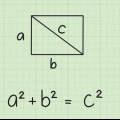
Jy kan die lengte van `n vertikale of horisontale lyn in `n koördinaatstelsel meet deur eenvoudig die koördinate by te voeg; dit is egter `n bietjie moeiliker om die lengte van `n diagonale lyn te meet. Jy kan die afstandformule gebruik om die lengte van so `n lyn te bepaal. Hierdie formule is eintlik die Pythagoras-stelling, wat duidelik word wanneer jy die lynstuk voorstel as die skuinssy van `n reghoekige driehoek. Deur `n eenvoudige meetkundige formule te gebruik, word die meet van lyne langs `n aantal koördinate `n relatief eenvoudige taak.
Trappe
Deel 1 van 2: Skryf die formule

1. Skryf die afstandformule neer. Die formule stel dit  , waardeur
, waardeur  is gelyk aan die afstand van die lyn,
is gelyk aan die afstand van die lyn,  is gelyk aan die koördinate van die eerste eindpunt van die lynstuk, en
is gelyk aan die koördinate van die eerste eindpunt van die lynstuk, en  is gelyk aan die koördinate van die tweede eindpunt van die lynstuk.
is gelyk aan die koördinate van die tweede eindpunt van die lynstuk.
 , waardeur
, waardeur  is gelyk aan die afstand van die lyn,
is gelyk aan die afstand van die lyn,  is gelyk aan die koördinate van die eerste eindpunt van die lynstuk, en
is gelyk aan die koördinate van die eerste eindpunt van die lynstuk, en  is gelyk aan die koördinate van die tweede eindpunt van die lynstuk.
is gelyk aan die koördinate van die tweede eindpunt van die lynstuk.
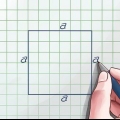
2. Bepaal die koördinate van die eindpunte van die lynstuk. Hierdie is dalk reeds gegee. Indien nie, tel langs die x-as en y-as om die koördinate te vind.
 .
. en nog een aan
en nog een aan  .
.
3. Pas die koördinate toe op die afstandformule. Maak seker dat jy die waardes vir die korrekte veranderlikes invoer. Die twee  -koördinate is binne die eerste hakies, en die twee
-koördinate is binne die eerste hakies, en die twee  -koördinate is binne die volgende twee hakies.
-koördinate is binne die volgende twee hakies.
 -koördinate is binne die eerste hakies, en die twee
-koördinate is binne die eerste hakies, en die twee  -koördinate is binne die volgende twee hakies.
-koördinate is binne die volgende twee hakies. en
en  , jou formule sal soos volg lyk:
, jou formule sal soos volg lyk: 
Deel 2 van 2: Berekening van die afstand

1. Bereken die minussom tussen hakies. Volgens die volgorde van bewerkings moet elke berekening tussen hakies eers bereken word.
- Byvoorbeeld:

2. Vierkant die waarde tussen hakies. Die volgorde van bewerkings sê dat jy dan die magte moet bereken.



3. Voeg die getalle onder die radikale teken by. Jy kan hierdie berekening doen asof jy met heelgetalle werk.



4. Los op vir d  . Om die finale antwoord te benader, vind die vierkantswortel van die som onder die radikaal.
. Om die finale antwoord te benader, vind die vierkantswortel van die som onder die radikaal.
 . Om die finale antwoord te benader, vind die vierkantswortel van die som onder die radikaal.
. Om die finale antwoord te benader, vind die vierkantswortel van die som onder die radikaal.
 eenhede.
eenhede.Wenke
- Moenie hierdie formule met ander verwar nie, soos die middelpuntformule, die hellingformule of die vergelyking van `n lyn.
- Hou die volgorde van bewerkings in gedagte wanneer die antwoord bereken word. Trek eers af, dan vierkant die verskil, tel dan op en bereken dan die vierkantswortel.
Artikels oor die onderwerp "Bereken die lengte van 'n lyn deur die afstandformule te gebruik"
Оцените, пожалуйста статью
Gewilde