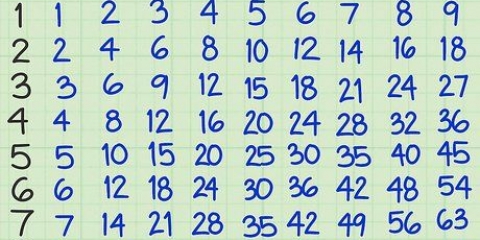
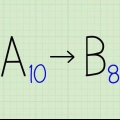In ons voorbeeld neem ons die vierkantswortels van 25 en 16. Sien onder: Sqrt(25×16) Sqrt(25) × Sqrt(16) 5 × 4 = 20 
Kom ons neem die vierkantswortel van 147 as `n voorbeeld. 147 is nie die produk van twee perfekte vierkante nie, so ons kan nie `n mooi heelgetalwaarde kry nie. Maar dit is die produk van `n perfekte vierkant en `n ander getal - 49 en 3. Ons kan hierdie inligting gebruik om ons antwoord in die eenvoudigste terme te skryf: sqrt(147) = Sqrt(49 × 3) = Sqrt(49) × Sqrt(3) = 7 × Sqrt(3) 
Kom ons keer terug na ons voorbeeld. Aangesien 2 = 4 en 1 = 1, weet ons dat Sqrt(3) tussen 1 en 2 is – waarskynlik nader aan 2 as 1. Ons skat dat 1.7. 7 × 1,7 = 11.9. As ons dit met die sakrekenaar nagaan, sien ons dat ons redelik naby aan die antwoord is: 12.13. Dit werk ook vir die groter getalle. Byvoorbeeld, Sqrt(35) is ongeveer tussen 5 en 6 (waarskynlik nader aan 6). 5 = 25 en 6 = 36. 35 is tussen 25 en 36, so die vierkantswortel sal tussen 5 en 6 wees. Aangesien 35 net onder 36 is, kan ons met `n mate van vertroue sê dat sy vierkantswortel net is laer as 6. Om met `n sakrekenaar na te gaan, gee ons `n antwoord van ongeveer 5,92 - ons was reg. 
`n Voorbeeld: ons bepaal die vierkantswortel van 45 deur hierdie metode te gebruik. Ons weet dat 45 = 9 × 5 en dat 9 = 3 × 3. Ons kan dus die vierkantswortel soos volg skryf: Sqrt(3 × 3 × 5). Verwyder net die 3`e en plaas `n 3 buite die radikaal om `n vereenvoudigde vierkantswortel te kry: (3)Sqrt(5). Nou kan jy maklik skat. `n Laaste voorbeeld; ons bepaal die vierkantswortel van 88: sqrt(88) = Sqrt(2 × 44) = Sqrt(2 × 4 × 11) = Sqrt(2 × 2 × 2 × 11). Ons het verskeie 2`e in ons vierkantswortel. Aangesien 2 priem is, kan ons `n paar verwyder en `n 2 buite die vierkantswortel plaas. = Ons vierkantswortel in eenvoudigste terme is (2) Sqrt(2 × 11) of (2) Sqrt(2) Sqrt(11). Nou kan ons Sqrt(2) en Sqrt(11) nader en `n geskatte antwoord vind, as ons wil. 

In ons voorbeeld is die syfer 7 heel links. Omdat ons weet dat 2 = 4 7 < 3 = 9, kan ons sê dat n = 2 omdat dit die grootste heelgetal is waarvan die vierkant kleiner as of gelyk is aan 7. Skryf 2 in die boonste regterkantste kwadrant. Dit is die eerste syfer van die antwoord. Skryf 4 (die vierkant van 2) in die regter onderste kwadrant. Hierdie nommer is belangrik vir die volgende stap. 
In ons voorbeeld skryf ons `n 4 onder 7 en trek dit af. Dit gee 3 as antwoord. 
In ons voorbeeld is die volgende getal "80". nota "80" langs die 3 in die linkerkwadrant. Vermenigvuldig dan die getal regs bo met 2. Hierdie getal is 2, dus 2 × 2 = 4. nota "`4"` regs onder, gevolg deur _×_=. 
In ons voorbeeld vul ons 8 in, en dit gee 4(8) × 8 = 48 × 8 = 384. Dit is meer as 380. So 8 is te groot, maar 7 is waarskynlik nie. Vul 7 in en los op: 4(7) × 7 = 329. 7 is goed, want 329 is kleiner as 380. Nota 7 regs bo. Dit is die tweede syfer in die vierkantswortel van 780.14. 
In ons voorbeeld trek ons 329 van 380 af, en dit gee 51 as gevolg. 
In ons antwoord skryf ons nou `n komma omdat ons dit ook in 780.14 teëkom. Beweeg die volgende paar (14) af in die linkerkwadrant. 27 x 2 = 54, so ons skryf "54 _×_=" in die onderste regter kwadrant. 
In ons voorbeeld, 549 × 9 = 4941, wat minder as of gelyk is aan die getal aan die linkerkant (5114). 549 × 10 = 5490, wat te hoog is, so 9 is ons antwoord. Skryf 9 as die volgende getal regs bo en trek die vermenigvuldigingsresultaat van die linkergetal af: 5114 -4941 = 173. 
Bereken die vierkantswortel van 'n getal sonder 'n sakrekenaar
Inhoud
Voor die koms van sakrekenaars moes beide studente en professore vierkantswortels met pen en papier bereken. Verskeie tegnieke is destyds ontwikkel om hierdie soms swaar taak aan te pak, met sommige wat `n rowwe skatting gee en ander wat die presiese waarde bereken. Lees verder om te leer hoe om die vierkantswortel van `n getal in `n paar maklike stappe te vind.
Trappe
Metode 1 van 2: Worteling met priemfaktore

1. Verdeel jou getal in vierkante. Hierdie metode gebruik die faktore van `n getal om die vierkantswortel van `n getal te vind (afhangende van die getal, kan dit `n presiese antwoord of `n skatting wees). Die faktore van `n gegewe getal is `n ewekansige reeks getalle wat saam vermenigvuldig word om daardie spesifieke getal te vorm. Byvoorbeeld, jy kan sê dat die faktore van 8 gelyk is aan 2 en 4 omdat 2 × 4 = 8. Volmaakte vierkante, aan die ander kant, is heelgetalle wat die produk van ander heelgetalle is. Byvoorbeeld: 25, 36 en 49 is perfekte vierkante omdat hulle onderskeidelik gelyk is aan 5, 6 en 7. Tweede arbeidsfaktore is, soos jy sal verstaan, faktore wat ook perfekte vierkante is. Om `n vierkantswortel te vind deur priemfaktore te gebruik, probeer eers om die getal in sy derdemagsfaktore te verdeel.
- Neem die volgende voorbeeld. Ons gaan die vierkantswortel van 400 vind. Om mee te begin, verdeel ons die getal in vierkante. Aangesien 400 `n veelvoud van 100 is, weet ons dat dit eweredig deelbaar is deur 25 - `n perfekte vierkant. Vinnige memorisering vertel ons dat 400 / 25 = 16. 16 is toevallig ook `n perfekte vierkant. So die kwadratiese faktore van 400 is 25 en 16 want 25 × 16 = 400.
- Ons skryf dit as: Sqrt(400) = Sqrt(25 × 16)

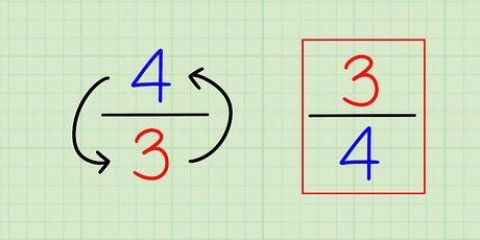
2. Neem die vierkantswortels van jou vierkantswortels. Die produkreël van vierkantswortels stel dit vir enige gegewe getal a en b, Sqrt(a × b) = Sqrt(a) × Sqrt(b). As gevolg van hierdie eienskap kan ons nou die vierkantswortels van die derdemagsfaktore neem en dit met mekaar vermenigvuldig vir die antwoord.

3. As jou nommer nie heeltemal perfek in berekening gebring kan word nie, vereenvoudig dit. In werklikheid sal die getalle waarvan jy die vierkantswortels wil vind nie mooi afgeronde getalle met mooi vierkantswortels soos 400 wees nie. In hierdie gevalle is dit dalk nie moontlik om `n heelgetal as `n antwoord te kry nie. In plaas daarvan, deur al die kubusse te gebruik wat jy kan vind, kan jy die antwoord bepaal as `n kleiner, makliker om te gebruik vierkantswortel. Jy doen dit deur die getal te verminder tot `n kombinasie van kubusfaktore en ander faktore, en dit dan te vereenvoudig.

4. Vereenvoudig, indien nodig. Deur die vierkantswortel in die eenvoudigste terme te gebruik, is dit gewoonlik redelik maklik om `n rowwe skatting van die antwoord te kry deur die oorblywende vierkantswortels te skat en dit te vermenigvuldig. Een manier om jou raaiskote te verbeter, is om die perfekte vierkante aan weerskante van die getal in jou vierkantswortel te vind. Jy weet dat die desimale waarde van die getal in jou vierkantswortel iewers tussen hierdie twee getalle is, dus moet jou raaiskoot ook tussen hierdie getalle wees.

5. Alternatiewelik, as `n eerste stap, kan jy die nommer vereenvoudig na dieminste gemene veelvoud. Die soektog na vierkantsfaktore is nie nodig as jy maklik die priemfaktore van `n getal kan vind nie (faktore wat terselfdertyd ook priemgetal is). Skryf die getal in terme van kleinste gemene veelvoude. Soek dan tussen jou faktore vir ooreenstemmende pare priemgetalle. As jy twee priemfaktore vind wat ooreenstem, verwyder hulle van die vierkantswortel en sit a van hierdie getalle buite die radikale.
Metode 2 van 2: Vind vierkantswortels sonder `n sakrekenaar
Met `n lang verdeling

1. Verdeel die syfers van jou nommer in pare. Hierdie metode is soortgelyk aan lang verdeling, wat jou toelaat om presies vind die vierkantswortel van `n getal syfer vir syfer. Alhoewel dit nie noodsaaklik is nie, kan die verdeling van `n getal in werkbare stukke dit makliker maak om op te los, veral as dit lank is. Trek eers `n vertikale lyn wat die werkarea in 2 areas verdeel, dan `n korter lyn naby die bokant van die regte area, verdeel dit in `n kleiner boonste deel en `n groter deel onder. Verdeel dan die getal in pare getalle, vanaf die desimale punt. Volgens hierdie reël word 79520789182.47897 gelyk aan "7 95 20 78 91 82.47 89 70". Skryf hierdie nommer in die boonste linker area.
- As `n voorbeeld, kom ons bereken die vierkantswortel van 780.14. Verdeel jou werkspasie soos hierbo aangedui en skryf neer "7 80, 14" in die boonste linkerhoek. Dit is goed as daar net een nommer heel links is, in plaas van twee. Jy skryf dan die antwoord (die vierkantswortel van 780.14) bo-aan die regte area neer.

2. Vind die grootste heelgetal n waarvan die vierkant kleiner as of gelyk is aan die syfer of getal heel links. Vind die grootste vierkant wat kleiner as of gelyk is aan hierdie getal, en vind dan die vierkantswortel van hierdie vierkant. Hierdie nommer is n. Let daarop dat in die boonste regterkantste area en skryf die vierkant van n in die onderste kwadrant van daardie area.

3. Trek die getal wat jy bereken het af van die syfer of nommer heel links. Soos met langdeling, is die volgende stap om die vierkant af te trek van die getal wat ons sopas gebruik het om te bereken. Skryf hierdie getal onder die nommer heel links en trek dit van mekaar af. Skryf die antwoord hieronder neer.

4. Skuif die volgende nommer af. Plaas dit langs die waarde wat jy in die vorige wysiging gevind het. Vermenigvuldig die getal regs bo met twee en skryf dit regs onder neer. Bespaar spasie langs die getal wat jy sopas neergeskryf het vir die vermenigvuldigingssom wat jy in die volgende stap sal doen. Skryf hier`"_×_="`.

5. Tik die nommers aan die regterkant in. In die leë spasie van die som (aan die regterkant), voer die grootste heelgetal in wat die resultaat van die vermenigvuldigingsom aan die regterkant minder as of gelyk aan die huidige getal aan die linkerkant sal maak.

6. Trek die getal wat jy pas bereken het af van die huidige getal aan die linkerkant. Dus trek jy die resultaat van die vermenigvuldiging aan die regterkant af van die huidige antwoord aan die linkerkant. Skryf jou antwoord direk hieronder.

7. Herhaal stap 4. Skuif die volgende paar getalle van 780.14 af. As jy by `n komma uitkom, skryf daardie komma in die antwoord aan die regterkant. Vermenigvuldig dan die getal regs bo met 2 en skryf die antwoord langs ("_ × _") soos hierbo.

8. Herhaal stappe 5 en 6. Vind die grootste getal wat `n antwoord kleiner as of gelyk aan die huidige getal aan die linkerkant gee. Los op.

9. Om die resultaat akkuraat te maak, herhaal die vorige prosedure totdat jy die antwoord kry met die aantal desimale (honderdes, duisendstes) wat jy nodig het.
Verstaan die prosedure
- Let daarop dat as jy 88962 deur 7 deel deur langdeling te gebruik, die eerste stap dieselfde is: jy het te doen met die eerste syfer van 88962 (8) en jy wil hê dat die grootste syfer vermenigvuldig met 7 minder as of gelyk aan 8 moet wees. In wese besluit jy d sodat 7×d ≤ 8 < 7×(d+1). In hierdie geval is d gelyk aan 1.
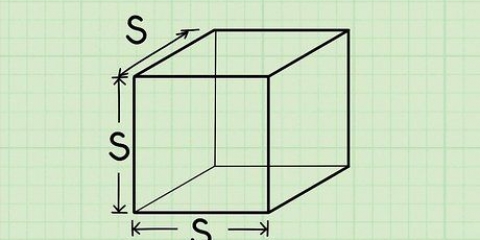
- In ons voorbeeld (10A+B)² = L = S = 100A² + 2×10A×B + B². Onthou dat 10A+B ons antwoord L verteenwoordig saam met B in die eenhede posisie, en A in die tiene posisie. Byvoorbeeld, as A=1 en B=2, dan is 10A+B die getal 12. (10A+B)² is die oppervlakte van die hele vierkant, terwyl 100A² is die oppervlakte van die grootste binneste vierkant, B² is die oppervlakte van die kleinste vierkant en 10A×B is die oppervlakte van elk van die oorblywende reghoeke. Deur hierdie lang, ingewikkelde prosedure kan ons die oppervlakte van die hele vierkant vind deur die oppervlaktes van die vierkante en reghoeke wat dit vorm by te voeg.

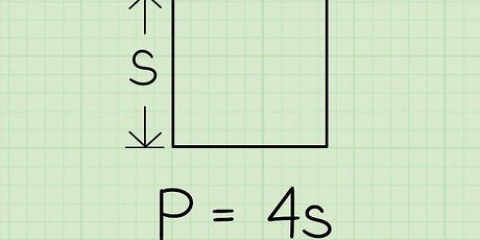
1. Beskou die getal wie se vierkantswortel jy wil bereken as die oppervlakte S van `n vierkant. Aangesien die oppervlakte van `n vierkant L is, waar L die lengte van een van sy sye is, so deur die vierkantswortel van jou getal te neem, probeer jy om die lengte L van die sy van daardie vierkant te bereken.

2. Gee elke syfer van jou antwoord `n letter. Gee die veranderlike A as die eerste syfer van L (die vierkantswortel wat ons probeer bereken). B is die tweede syfer, C is die derde, ensovoorts.

3. Gee vir elkeen `n brief "paar getalle" van die nommer waarmee jy begin. Gee die veranderlike Sa na die eerste paar syfers in S (die beginwaarde), Sb na die tweede syferpaar, ens.

4. Verstaan die verband tussen hierdie metode en lang verdeling. Hierdie metode om `n vierkantswortel te vind is in wese langdeling, deur die aanvanklike waarde deur sy vierkantswortel te deel en die vierkantswortel as die antwoord te neem "datum". Soos met langdeling, waar jy net in die volgende syfer op `n slag belangstel, stel jy net belang in die volgende twee syfers op `n slag (wat ooreenstem met die volgende syfer van die vierkantswortel).

5. Vind die grootste getal waarvan die vierkant kleiner as of gelyk is aan Sa is. Die eerste syfer A in ons antwoord is dan die grootste heelgetal waarvan die vierkant nie groter as S is niea (A sodanig dat A² ≤ Sa < (A+1)²). In ons voorbeeld is Sa = 7, en 2² ≤ 7 < 3², dus A = 2.

6. Visualiseer die vierkant waarvan jy die oppervlakte wil vind. Jou antwoord, die vierkantswortel van die beginwaarde, is L, wat die lengte van `n vierkant van area S (die beginwaarde) beskryf. Die waardes vir A, B en C verteenwoordig die getalle in die waarde L. Nog `n manier om dit te sê is dat vir `n 2-syfer-antwoord, 10A + B = L, en vir `n 3-syfer-antwoord, 100A +10B + C = L, ensovoorts.

7. Trek A² van S afa. Bring `n paar getalle (Sb) af van die nommer S. sa sb is amper die totale oppervlakte van die vierkant, waarvan jy net die oppervlakte van die grootste binneste vierkant afgetrek het. Die res is sê die getal N1, wat ons in stap 4 gekry het (N1 =380 in ons voorbeeld). N1 is gelyk aan 2×10A×B + B² (die oppervlakte van die 2 reghoeke plus die oppervlakte van die klein vierkant).

8. Kyk na N1 = 2×10A×B + B², ook geskryf as N1 = (2×10A + B) × B. In ons voorbeeld ken jy reeds N1 (380) en A (2), so nou moet jy B vind. B is waarskynlik nie `n heelgetal nie, so jy moet eintlik vind die grootste heelgetal B, sodat (2×10A + B) × B ≤ N1. So nou het jy: N1 < (2×10A + (B+1)) × (B+1).)

9. Los die vergelyking op. Om hierdie vergelyking op te los, vermenigvuldig A met 2, skuif dit na die tiene (vermenigvuldig met 10), plaas B in die eenhede en vermenigvuldig die resultaat met B. Met ander woorde, (2×10A + B) × B. Dit is presies wat jy doen wanneer jy skryf "N_×_=" (met N=2×A) in die onderste regterkwadrant in stap 4. In stap 5 bepaal jy die grootste heelgetal B wat onder die lyn pas, sodat (2×10A + B) × B ≤ N1.

10. Trek die oppervlakte (2×10A + B) × B van die totale oppervlakte af. Dit lewer die oppervlakte S-(10A+B)² wat jy nog nie in ag geneem het nie (en wat jy gebruik om die volgende getalle op dieselfde manier te bereken).

11. Om die volgende syfer C te bereken, herhaal die prosedure. Beweeg die volgende paar getalle van S af na onder (Sc) om N2 aan die linkerkant te kry, en soek die grootste C sodat jy nou het: (2×10×(10A+B)+C) × C ≤ N2 (gelyk aan twee keer die tweesyfergetal "A B" gevolg deur "_×_=" . Bepaal nou die grootste getal wat jy hier kan invoer, wat jou `n antwoord sal gee wat minder as of gelyk is aan N2.
Wenke
- Deur die desimale punt twee plekke te skuif (`n faktor van 100) skuif die desimale punt in die ooreenstemmende vierkantswortel met een plek (`n faktor van 10).
- In die voorbeeld kan 1.73 beskou word as "rus": 780,14 = 27,9² + 1,73.
- Hierdie metode werk vir enige getallestelsel, nie net die desimale (tien desimale) stelsel nie.
- Plaas gerus die berekeninge waar jy wil. Sommige mense skryf dit bo die getal waarvan hulle die vierkantswortel wil bereken.
- `n Alternatiewe metode is die volgende: √z = √(x^2+y) = x + y/(2x + y/(2x + y/(2x) + ...))). Byvoorbeeld, om die vierkantswortel van 780.14 te bereken, sal jy die heelgetal kwadraat naaste aan 780.14 (28) neem, dus =780.14, x=28 en y=-3.86. Deur in te vul en te skat gee ons x + y/(2x) en dit gee (vereenvoudigde terme) 78207/2800 of ongeveer 27,931(1); die volgende kwartaal, 4374188/156607 of ongeveer 27.930986(5). Elke term voeg ongeveer 3 desimale plekke van akkuraatheid by die vorige een.
Waarskuwings
- Maak seker dat jy die getal in pare verdeel vanaf die desimale punt. Verdeling 79520789182.47897 as "79 52 07 89 18 2.4 78 97" gee `n resultaat wat nie korrek is nie.
Artikels oor die onderwerp "Bereken die vierkantswortel van 'n getal sonder 'n sakrekenaar"
Оцените, пожалуйста статью
Gewilde