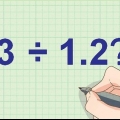Pas 15 in 34? Ja, seker, en so kan ons die antwoord begin bereken. (Die eerste getal hoef nie perfek te pas nie, dit moet net kleiner as die tweede getal wees). 
Ons moet 34 ÷ 15 oplos, of `hoeveel keer gaan 15 in 34`? Jy soek `n getal wat jy met 15 kan vermenigvuldig om `n getal te kry wat minder as 34 is, maar redelik naby: Werke 1? 15 x 1 = 15, dit is minder as 34, maar hou aan raai. Werke 2? 15 x 2 = 30. Dit is steeds minder as 34, so 2 is `n beter antwoord as 1. Werke 3? 15 x 3 = 45, groter as 34. Te hoog! Die antwoord is 2. 
Aangesien jy 34 ÷ 15 bereken, sal jy as antwoord, 2, op die antwoordreël bokant die `4` skryf. 
Jou antwoord was 2 en die kleiner getal in die probleem is 15, so ons bereken 2 x 15 = 30. Skryf `30` onder `34`. 
Los 34 – 30 op en skryf die antwoord hieronder op `n nuwe reël. Die antwoord is 4. Hierdie 4 is steeds `die res` nadat 34 deur 15 twee keer gedeel is, so ons sal dit in die volgende stap gebruik. 
Los die 4 waar dit is en bring die `7` van `3472` af om 47 te maak. 
Ons los op: 47 ÷ 15: 47 is groter as ons laaste getal, so die antwoord sal groter wees. Kom ons probeer vier: 15 x 4 = 60. Nee, te groot! In plaas daarvan probeer ons drie: 15 x 3 = 45. Kleiner as 47 maar naby daaraan. Perfek. Die antwoord is 3, so ons skryf dit bo die `7` op die antwoordreël. (Sou ons eindig met `n som soos 13 ÷ 15, waar die eerste getal kleiner is, moet ons `n derde syfer afneem voordat ons dit kan oplos). 
Onthou, ons het 47 ÷ 15 = 3 bereken, en wil nou vind wat oor is: 3 x 15 = 45, skryf dus `45` onder 47. 47 - 45 = 2. Skryf `2` onder 45. 
Die volgende probleem is 2 ÷ 15, wat nie veel sin maak nie. Bring `n getal af om dit 22 ÷ 15 te maak. 15 gaan een keer in 22, so ons skryf `1` as die laaste syfer van die antwoord. Ons antwoord is nou 231. 
1 x 15 = 15, skryf dus 15 onder 22. Bereken 22 - 15 = 7. Daar is nie meer getalle om af te haal nie, so in plaas daarvan om aan te hou deel skryf ons `rus 7` na ons antwoord. Die finale antwoord: 3472 ÷ 15 = 231 res 7.


As jy dit moeilik vind, tel net in drievoud en voeg `n 0 aan die einde by. Tel totdat jy hoër is as die grootste getal in die probleem (143), en stop daar. 
30 (een vinger), 60 (twee vingers), 90 (drie vingers), 120 (vier vingers). dus 30 x vier = 120. 150 (vyf vingers), dus 30 x vyf = 150. 4 en 5 is die twee mees waarskynlike antwoorde op ons probleem. 
27 x 4 = 108 27 x 5 = 135 
27 x 6 = 162. Dit is hoër as 143, so dit kan nie die regte antwoord wees nie. 27 x 5 het die naaste gekom sonder om oor te gaan, dus 143 ÷ 27 = 5 (plus `n res 8, want 143-135 = 8).
Deel deur 'n getal met twee of meer syfers
Inhoud
Deling deur `n getal met twee of meer syfers is baie soortgelyk aan langdeling met een syfer, maar dit neem `n bietjie langer en verg `n bietjie meer oefening. Aangesien die meeste van ons nie die tabel van 47 onthou nie, verg dit `n bietjie raaiwerk, maar daar is `n netjiese truuk wat jy kan leer om dit vinniger te doen. Dit word ook makliker met bietjie oefening, so moenie gefrustreerd raak as dit aanvanklik stadig lyk nie.
Trappe
Deel 1 van 2: Deling deur `n tweesyfergetal

1. Kyk na die eerste syfer van die groter getal. Skryf die probleem as langafdeling. Soos `n eenvoudiger deelprobleem, kyk jy basies na die kleiner getal en vra jouself af: "Pass dit in die eerste syfer van die groter getal??`
- Gestel jy het die probleem 3472 ÷ 15. Pas 15 in 3? Aangesien 15 beslis groter as 3 is, is die antwoord `nee` en kom ons gaan aan na die volgende stap.

2. Kyk na die eerste twee getalle. Aangesien `n tweesyfergetal nie in `n eensyfergetal kan inpas nie, kom ons kyk nou na twee syfers, net soos ons sou met `n gereelde deelprobleem. As dit steeds onmoontlik is om te verdeel, sal jy na die eerste drie syfers moet kyk, maar in ons voorbeeld is dit nie nodig nie:

3. Gebruik bietjie raaiwerk. Kyk hoeveel keer die eerste nommer in die ander pas. Jy ken dalk reeds die antwoord, maar indien nie, maak `n skatting en kontroleer jou antwoord met `n vermenigvuldiging.

4. Skryf die antwoord bo die laaste nommer wat jy gebruik het. Om dit as `n lang verdeling te skryf, behoort bekend te voel.

5. Vermenigvuldig jou antwoord met die kleiner getal. Dit is dieselfde as normale langdeling, maar hier gebruik ons `n tweesyfergetal.

6. Trek beide getalle van mekaar af. Die laaste ding wat jy geskryf het, het onder die oorspronklike groter nommer (of deel daarvan) gegaan. Behandel dit as `n minussom en skryf die antwoord daaronder op `n nuwe reël neer.

7. Bring die volgende nommer af. Net soos `n gewone deelprobleem, hou ons aan om die volgende syfer van die antwoord te bereken totdat ons klaar is.

8. Los die volgende subprobleem op. Om die volgende nommer te kry, herhaal dieselfde stappe as hierbo vir die nuwe probleem. Jy kan teruggaan na skatting om die antwoord te vind:

9. Gaan voort met lang verdeling. Herhaal langdeling soos ons voorheen gedoen het om ons antwoord met die kleiner getal te vermenigvuldig, skryf die resultaat onder die groter getal neer en trek dit af vir die volgende res.

10. Bepaal die laaste syfer. Soos voorheen bring ons die volgende syfer van die oorspronklike probleem af sodat ons die volgende subprobleem kan oplos. Herhaal die stappe hierbo totdat jy elke syfer van die antwoord kry.

11. Bepaal die res. Nou net `n minus bedrag vir die vind van die laaste rus, en ons is klaar. Trouens, as die antwoord op die minus som 0 is, hoef jy glad nie `n res te skryf nie.

Deel 2 van 2: Leer om goed te skat

1. Rond af tot die naaste tien. Dit is nie altyd maklik om te sien hoeveel keer `n tweesyfergetal in `n groter getal pas nie. `n Handige truuk is om af te rond tot die naaste veelvoud van 10 om raai makliker te maak. Dit is nuttig vir kleiner deling probleme, of lang deling.
- Byvoorbeeld, kom ons sê ons moet 143 ÷ 27 oplos, maar ons weet nie hoeveel keer 27 in 143 ingaan nie. Kom ons maak dan asof ons 143 ÷ 30 moet oplos.

2. Tel die kleiner getal op jou vingers. In ons voorbeeld kan ons begin bereken met 30 en nie met 27 nie. Om in stappe van 30 te tel is redelik maklik as jy dit eers onder die knie het: 30, 60, 90, 120, 150.

3. Bepaal die twee mees waarskynlike antwoorde. Die getal het nie presies by 143 gepas nie, maar ons ken wel getalle wat naby is: 120 en 150. Kom ons kyk hoeveel vingers ons moet tel om daar te kom:

4. Toets daardie twee getalle met die werklike probleem. Noudat ons twee goeie raaiskote het, kan ons hulle toets op die oorspronklike probleem, 143 ÷ 27:

5. Maak seker jy kan nie nader kom nie. Aangesien beide getalle onder 143 eindig, kan ons probeer om nog nader te kom deur nog een vermenigvuldiging te probeer:

Wenke
- As jy nie met die hand wil vermenigvuldig tydens langdeling nie, probeer om die probleem in getalle te verdeel en elke deel uit die kop op te los. Byvoorbeeld, 14 x 16 = (14 x 10) + (14 x 6). Skryf 14 x 10 = 140 neer sodat jy nie vergeet nie. Dan: 14 x 6 = (10 x 6) + (4 x 6). 10 x 6 = 60 en 4 x 6 = 24. Doen 140 + 60 + 24 = 224 en jy het die antwoord.
Waarskuwings
- As jou minus-som op enige tydstip `n getal groter as die deler tot gevolg het, dan was jou skatting nie hoog genoeg nie. Vee daardie hele stap uit en probeer groter skat.
- As jou minus op enige tydstip gelei het tot `n negatief getal, dan was jou skatting te hoog. Vee daardie hele stap uit en probeer kleiner skat.
Ander hulpbronne
Artikels oor die onderwerp "Deel deur 'n getal met twee of meer syfers"
Оцените, пожалуйста статью
Gewilde