Dit binêre (basis 2) getallestelsel het twee moontlike waardes, gewoonlik voorgestel as 0 of 1, vir elke posisie in `n getal. Die verskil met die desimale (basis 10) getallestelsel is dat daar tien moontlike waardes (0,1,2,3,4,5,6,7,8 of 9) vir elke posisie is.
Om verwarring te voorkom wanneer verskillende getallestelsels gebruik word, kan die basis van `n getal aangedui word deur dit na die nommer in te teken.Byvoorbeeld, die binêre getal 10011100 kan na basis 2 geskryf word deur dit as 10011100 te skryf2.Die desimale getal 156 kan as 156 geskryf word10 of ten volle as "honderd ses en vyftig, basis 10".
Aangesien die binêre stelsel die masjientaal van rekenaars is, moet ernstige programmeerders ten volle verstaan hoe om binêre getalle na desimale getalle om te skakel.Omskakeling in die omgekeerde rigting, van desimale na binêre, is dikwels moeiliker om eers te leer.
Let wel: Dit gaan SLEGS oor berekeninge en nie ASCII-vertalings nie.
Trappe
Metode 1 van 2: Posisiestelselmetode
1. In hierdie voorbeeld gaan ons die binêre getal 10011011 gebruik2 omskakel na desimale. Lys die magte van twee van regs na links. Begin met 2, dit het die waarde "1".Vermenigvuldig die eksponente met 1 vir elke mag.Stop wanneer die aantal elemente in die lys gelyk is aan die aantal syfers in die binêre getal. Die voorbeeldnommer, 10011011, het 8 syfers, so die lys sal soos volg lyk: 128, 64, 32, 16, 8, 4, 2, 1
2. Skryf die binêre getal onder die lys neer.
3. Verbind binêre getalle met magte van twee. Trek lyne wat elke binêre syfer verbind met die ooreenstemmende tweede mag daarbo.Begin by die eerste binêre syfer, van regs, en gaan voort totdat jy al die binêre syfers en die magte verbind het.
4. Gaan deur al die syfers van die binêre getal. As die getal `n 1 is, skryf die ooreenstemmende tweede mag onder die lyn, direk onder die getal.As die getal `n 0 is, skryf `n 0 onder die lyn.
5. Tel die getalle onder die lyn bymekaar. Die som moet 155 wees. Dit is die desimale ekwivalent van die binêre getal 10011011.Of, geskryf met die basis in subskripsie:
6. As jy hierdie metode gereeld herhaal, sal jy vind dat jy die kragte van twee beter onthou, sodat jy stap 1 kan oorslaan.
Metode 2 van 2: Verdubbelingsmetode
1. Hierdie metode gebruik nie magte nie. Daarom is dit beter as jy groter getalle uit die kop wil omskakel, aangesien jy net die subtotaal hoef te onthou.
2. Begin met die syfer heel links van die gegewe binêre getal. Vir elke daaropvolgende getal van links na regs, verdubbel die vorige totaal en voeg dit by die huidige getal. Byvoorbeeld, om die nommer 1011001 in te voer2 om na desimale om te skakel, neem ons die volgende stappe:
3. 1011001 → 0 * 2 + 1 = 1
4. 1011001 → 1 * 2 + 0 = 2
5. 1011001 → 2 * 2 + 1 = 5
6. 1011001 → 5 * 2 + 1 = 11
7. 1011001 → 11 * 2 + 0 = 22
8. 1011001 → 22 * 2 + 0 = 44
9. 1011001 → 44 * 2 + 1 = 8910
10. Soos die posisiestelselmetode, kan hierdie metode gewysig word om van enige getallestelsel na `n desimale getal om te skakel.Verdubbeling word hier gebruik omdat die basis twee is. As die gegewe getal `n ander basis het, gebruik dit in plaas van 2. Byvoorbeeld, as die getal `n basis van 37 het, ruil *2 met *37 om. Die resultaat sal altyd `n desimale getal wees (basis 10). :)
Wenke
- Oefen baie. Probeer die binêre getalle 110100012, 110012, en 111100012.Hul desimale ekwivalente is 20910, 2510, en 24110.
- Die sakrekenaar wat saam met Microsoft Windows kom kan ook hierdie omskakeling vir jou doen, maar as jy `n programmeerder is, is dit beter dat jy `n goeie begrip het van hoe hierdie omskakeling werk. Die opsies van hierdie sakrekenaar kan gevind word deur die "Beskou" spyskaart en dan "Wetenskaplik" (of "programmeerder"). Met Linux kan jy gebruik galkulator.
Waarskuwings
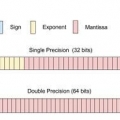
- Dit kan gebruik word vir ongetekende binêr (slegs positiewe getalle), maar nie vir getekende, drywende punt of vaste punt nie.
Artikels oor die onderwerp "Omskakeling van 'n binêre getal in 'n desimale getal"