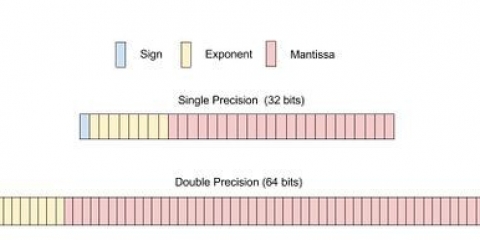
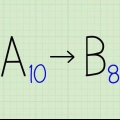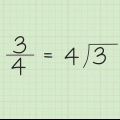16 = 1.048.576 16 = 65.536 16 = 4.096 16 = 256 16 = 16 As die desimale getal wat jy omskakel groter as 1 is.048.576, bereken dan die hoër magte van 16 en voeg dit by die lys. 
Byvoorbeeld, as jy 495 skakel om na heksadesimale, kies dan 256 uit die lys hierbo. 
In ons voorbeeld is 495 ÷ 256 = 1.93... , maar ons stel net belang in die hele getal 1. Jou antwoord is die eerste syfer van die heksadesimale getal. In hierdie geval, aangesien ons deur 256 gedeel het, is die 1 die getal in die plek van die "256-af." 
Vermenigvuldig jou laaste antwoord met die deler. In ons voorbeeld is 1 x 256 = 256. (Met ander woorde, die 1 van ons heksadesimale getal verteenwoordig die 256 met die basis 10). Trek jou antwoord van die dividend af. 495 - 256 = 239. 
239 ÷ 16 = 14. Weereens, ons ignoreer alle desimale plekke. Dit is die tweede syfer van ons heksadesimale getal, die "16-en." Enige getal van 0 tot 15 kan as `n enkele heksadesimale syfer voorgestel word. Ons skakel om na die korrekte notasie aan die einde van hierdie metode. 
14 x 16 = 224. 239 - 224 = 15, dus die res is 15. 
Die laaste "figuur" van ons heksadesimale getal is 15, in die plek van die "eenhede." 
Die getalle 0 tot 9 bly dieselfde. 10 = A; 11 = B; 12 = C; 13 = D; 14 = E; 15 = F In ons voorbeeld eindig ons met die getalle (1)(14)(15). In behoorlike notasie word dit die heksadesimale getal 1EF. 
1EF → (1)(14)(15) Van regs na links is 15 in 16 = 1ste posisie. 15 x 1 = 15. Die volgende syfer van links is in die 16 = 16de posisie. 14 x 16 = 224. Die volgende syfer is in die 16 = 256ste posisie. 1 x 256 = 256. Ons tel hulle almal bymekaar, 256 + 224 + 15 = 495, ons oorspronklike nommer. 

Om die res te vind, vermenigvuldig die antwoord met die deler en trek dan die resultaat van die dividend af. In ons voorbeeld, 317.547 - (19.846 x 16) = 11. Skakel die syfer om na heksadesimale formaat deur die kleingetalomskakelingstabel bo-aan hierdie artikelbladsy te gebruik. 11 draaie B in ons voorbeeld. 
In ons voorbeeld, 19.846 / 16 = 1.240. res = 19.846 - (1.240 x 16) = 6. Dit is die tweede tot laaste syfer van ons heksadesimale getal. 
Neem die laaste kwosiënt en deel dit weer deur 16. 1.240 / 16 = 77 res 8. 77 / 16 = 4 res 13 = d. 4 < 16, so 4 is die eerste syfer. 
Ons laaste antwoord is 4D86B. Om jou werk na te gaan, skakel elke syfer terug na die desimale getal, vermenigvuldig met magte van 16, en tel die resultate bymekaar. (4 x 16) + (13 x 16) + (8 x 16) + (6 x 16) + (11 x 1) = 317.547, ons oorspronklike desimale getal.
Skakel van desimale na heksadesimale
Inhoud
Heksadesimale is `n getallestelsel met die basis sestien. Dit beteken daar is 16 simbole om `n getal aan te dui, met A, B, C, D, E en F bygevoeg by die gewone tien syfers. Omskakeling van desimale na heksadesimale is moeiliker as andersom. Neem die tyd om dit te leer, want dit is makliker om foute te vermy sodra jy verstaan hoekom die omskakeling werk.
Kleingetal-omskakelings
| Desimale | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Heksadesimale | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | B | C | d | E | f |
Trappe
Metode 1 van 2: Intuïtiewe metode

1. Gebruik hierdie metode as jy nuut is met heksadesimale getalle. Van die twee benaderings in hierdie artikel is dit die maklikste vir die meeste mense om te volg. As jy reeds vertroud is met die verskillende basisse, probeer die vinniger een metode soos hieronder aangedui.
- As jy heeltemal onbekend is met heksadesimale getalle, leer eers die basiese konsepte.

2. Skryf die magte van 16 neer. Elke syfer binne die heksadesimale stelsel verteenwoordig `n ander mag van 16, net soos `n desimale syfer `n mag van 10 is. Hierdie lys van magte van 16 sal handig te pas kom by die omskakeling:

3. Vind die hoogste mag van 16 wat binne die desimale getal pas. Skryf die desimale getal neer wat jy wil omskakel. Gebruik bogenoemde lys as verwysing. Vind die hoogste mag van 16 wat minder is as die desimale getal.

4. Verdeel die desimale getal met hierdie mag van 16. Stop by die heelgetal en ignoreer elke syfer na die desimale punt van die antwoord.

5. Soek die res. Dit vertel jou wat oor is van die desimale getal wat omgeskakel moet word. Dit is hoe jy dit kan bereken, net soos met `n lang afdeling:

6. Deel die res deur die volgende hoër mag van 16. Gebruik jou lys van magte van 16 weer as verwysing. Gaan so voort tot die minste krag van 16. Deel die res deur daardie waarde om die volgende syfer van jou heksadesimale getal te vind. (As die res minder as hierdie getal is, is die volgende syfer 0.)

7. Bepaal weer die res. Soos voorheen, vermenigvuldig die antwoord met die deler en trek dit van die dividend af. Dit is die res wat nog omgeskakel moet word.

8. Herhaal totdat jy `n res van minder as 16 het. Sodra die res 0 tot 15 is, kan dit met `n enkele heksadesimale syfer uitgedruk word. Skryf dit as die laaste nommer.

9. Skryf jou antwoord in die korrekte notasie. Jy weet nou wat al die syfers van jou heksadesimale getal is. Maar tot dusver het ons hulle net in basis tien geskryf. Om elke syfer in die korrekte heksadesimale notasie te skryf, skakel hulle om deur hierdie gids te gebruik:

10. Gaan jou werk na. Dit is maklik om jou antwoord na te gaan as jy verstaan hoe heksadesimale getalle werk. Skakel elke syfer terug na desimale vorm, en vermenigvuldig dit met die 16de mag vir daardie basisposisie. Hier is wat ons moet doen vir ons voorbeeld:
Metode 2 van 2: Vinnige metode (met rus)

1. Deel die desimale getal deur 16. Behandel hierdie verdeling as `n heelgetalafdeling. Met ander woorde, jy stop by `n antwoord met `n heelgetal, in plaas daarvan om die desimale getalle te bereken.
- Kom ons wees `n bietjie meer ambisieus oor hierdie voorbeeld, en die desimale getal 317.547 omskep. Bereken 317.547 ÷ 16 = 19.846, en ignoreer die desimale.

2. Skryf die res in heksadesimale notasie. Noudat jy die getal deur 16 gedeel het, is die res die deel wat nie meer by die posisie van die 16`e of hoër pas nie. Daarom moet die res na die posisie van die eenhede kom, dit laaste syfer van die heksadesimale getal.

3. Herhaal hierdie proses met die kwosiënt. Jy het die res na `n heksadesimale syfer omgeskakel. Om nou voort te gaan om die kwosiënt om te skakel, deel dit weer deur 16. Die res is die tweede tot laaste syfer van die heksadesimale getal. Dit werk met dieselfde logika as hierbo: die oorspronklike getal word nou gedeel deur (16 x 16 =) 256, so die res is die deel van die getal wat by die posisie van die 256`e pas. Ons ken reeds die eenhede, die res moet in die plek van die 16`s wees.

4. Herhaal totdat jy `n kwosiënt minder as 16 kry. Moenie vergeet om `n res van 10 na 15 in heksadesimale formaat om te skakel nie. Let op enige rus langs die pad. Die laaste kwosiënt (minder as 16) is die eerste syfer van jou nommer. Ons gaan voort met die voorbeeld:

5. Voltooi die nommer. Soos voorheen genoem, bepaal jy elke syfer van die heksadesimale getal van regs na links. Gaan jou werk na om seker te maak jy het dit in die regte volgorde geskryf.
Wenke
- Om verwarring te voorkom wanneer die verskillende numeriese stelsels gebruik word, kan jy die basis as `n subskripsie skryf. Byvoorbeeld, 51210 is dan "512 met basis 10," `n gewone desimale getal. 51216 beteken "512 met basis 16," gelykstaande aan die desimale getal 1.29810.
Artikels oor die onderwerp "Skakel van desimale na heksadesimale"
Оцените, пожалуйста статью
Gewilde