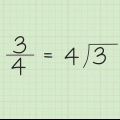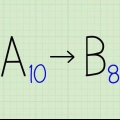Skakel 'n herhalende desimale om na 'n breuk: 9 stappe (met prente)

Inhoud

Trappe
- Deel1 van 2: Omskakeling van eenvoudige herhalende desimale
- Deel 2 van 2: Omskakeling van getalle met herhalende en nie-herhalende desimale

`n Herhalende desimale, ook genoem `n herhalende desimale, is `n desimale getal wat `n syfer of groep syfers bevat wat onbepaald met gereelde intervalle herhaal. Herhaalde desimale kan moeilik wees om mee te werk, maar hulle kan ook na `n breuk omgeskakel word. Soms word herhalende desimale met `n lyn bokant die herhalende syfers aangedui. Die getal 3,7777 met 7 as `n herhalende syfer kan byvoorbeeld ook as 3 geskryf word.7. Om `n getal soos hierdie na `n breuk om te skakel, skryf dit as `n vergelyking, vermenigvuldig en trek af om die herhalende desimale te verwyder, en los die vergelyking op.

Trappe

Deel1 van 2: Omskakeling van eenvoudige herhalende desimale

Prent getiteld Skakel herhalende desimale om na breuke Stap 1

1. Vind die herhalende desimale. Byvoorbeeld: die nommer 0,4444 het `n herhalende desimaal 4. Dit is `n standaard herhalende desimale in die sin dat daar geen nie-herhalende deel in die desimale getal is nie. Tel hoeveel herhalende (herhalende) desimale plekke daar in die patroon is.

Wanneer jou vergelyking geskryf is, vermenigvuldig dit met 10^j`, waardeury is gelyk aan die aantal herhalende syfers in die patroon.
In die voorbeeld van 0.4444 is daar een syfer wat herhaal, so jy vermenigvuldig die vergelyking met 10^1.
Vir `n herhalende desimale van 0,4545, daar is twee getalle wat herhaal, en jy sal dus jou vergelyking met 10^2 vermenigvuldig.
Vir drie herhalende getalle, vermenigvuldig met 10^3, ens.

Prent getiteld Skakel herhalende desimale om na breuke Stap 2

2. Herskryf die desimale as `n vergelyking. Skryf dit so dat x gelyk is aan die oorspronklike getal.In hierdie geval is die vergelyking x = 0.4444. Aangesien daar net een syfer in die herhalende desimale is, vermenigvuldig die vergelyking met 10^1 (wat gelyk is aan 10).

In die voorbeeld: waar x = 0,4444, dan 10x = 4,4444.

In die voorbeeld x = 0,4545 daar is twee herhalende getalle, so jy vermenigvuldig beide kante van die vergelyking met 10^2 (wat gelyk is aan 100), wat jou 100x = 45.4545 kry.

Prent getiteld Skakel herhalende desimale om na breuke Stap 3

3. Verwyder die herhalende desimale. Jy doen dit deur x van 10x af te trek. Onthou dat wat jy aan die een kant van die vergelyking doen, jy aan die ander kant moet doen, dus:

10x – 1x = 4,4444 – 0,4444

Aan die linkerkant het jy 10x - 1x = 9x. Aan die regterkant het jy 4.4444 – 0.4444 = 4

Daarom: 9x = 4

Prent getiteld Skakel herhalende desimale om na breuke Stap 4

4. Los op vir x. Sodra jy weet wat 9x gelyk is, kan jy bepaal wat x gelyk is deur beide kante van die vergelyking deur 9 te deel:

Aan die linkerkant van die vergelyking wat jy het 9x ÷ 9 = x. Aan die regterkant van die vergelyking wat jy het 4/9

Dit is hoekom x = 4/9, en kan die herhalende desimale wees 0,4444 as die breuk geskryf word 4/9.

Prent getiteld Skakel herhalende desimale om na breuke Stap 5

5. Verminder die breuk. Skakel die breuk om na sy eenvoudigste vorm (indien enige) deur beide die teller en noemer deur die grootste gemene faktor te deel.

In die voorbeeld van 4/9 is dit die eenvoudigste vorm.

Deel 2 van 2: Omskakeling van getalle met herhalende en nie-herhalende desimale

Prent getiteld Skakel herhalende desimale om na breuke Stap 6

1. Bepaal die herhalende getalle. Dit is nie ongewoon dat `n getal nie-herhalende syfers voor die herhalende desimale het nie, maar dit kan steeds na breuke omgeskakel word.

Neem byvoorbeeld die nommer 6,215151. Hier is 6.2 nie-herhalend, en die herhalende getalle is 15.
Let weer op hoeveel herhalende syfers in die patroon is, want jy gaan vermenigvuldig met 10^y gebaseer op daardie getal.
In hierdie voorbeeld is daar twee herhalende getalle, so vermenigvuldig die vergelyking met 10^2.

Prent getiteld Skakel herhalende desimale om na breuke Stap 7

2. Skryf die probleem as `n vergelyking en trek die herhalende desimale af. Weereens, as x = 6,215151, dan 100x = 621,5151. Om die herhalende desimale te verwyder, trek van beide kante van die vergelyking af:

100x – x (= 99x) = 621,5151 – 6,215151 (= 615.3)

Dus, 99x = 615.3

Prent getiteld Skakel herhalende desimale om na breuke Stap 8

3. Los op vir x. Aangesien 99x = 615.3, deel beide kante van die vergelyking deur 99. Dit gee jou x = 615.3/99.

Prent getiteld Skakel herhalende desimale om na breuke Stap 9

4. Verwyder die desimale in die toonbank. Doen dit deur die teller en noemer met te vermenigvuldig 10^z`, waardeurZ is gelyk aan die aantal desimale wat jy moet skuif om die desimale uit te skakel. In 615.3 moet jy die desimale een posisie skuif, wat beteken jy vermenigvuldig die teller en noemer met 10^1:

615,3×10 / 99 x 10 = 6153/990

Vereenvoudig die breuk deur die teller en noemer deur die grootste gemene faktor (in hierdie geval 3) te deel, en jy kry x = 2,051 / 330