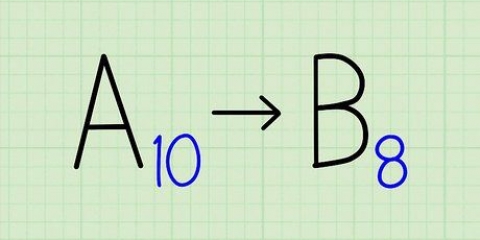Skakel binêre na heksadesimale om: 12 stappe (met prente)

Inhoud

Trappe
- Metode 1 van 2: Maklike omskakelings
- Metode 2 van 2: Skakel langer binêre stringe om
Wenke
Waarskuwings

Hierdie artikel sal verduidelik hoe om binêre getalle (basis 2) om te skakel na heksadesimale getalle (basis 16). Of dit nou programmering is, as huiswerk vir wiskunde, of vir Die marsman, Heksadesimale getalle is nuttig en `n kragtige vinnige tegniek wanneer lang binêre stringe geskryf word. Omdat beide basisse magte van 2 is, is hierdie prosedure baie eenvoudiger as ander omskakelings, soos omskakel van desimale na binêre. Al wat jy nodig het om `n binêre getal na `n heksadesimale getal om te skakel, is `n paar basiese wiskunde- en telvaardighede.

Trappe

Metode 1 van 2: Maklike omskakelings

Prent getiteld Skakel Binêr na Heksadesimale Stap 1 om

1. Neem `n string van tot vier binêre getalle om om te skakel. Binêre getalle kan slegs 1 of 0 wees. Heksadesimale getalle kan 0-9 of A-F wees omdat heksadesimale getalle basis 16 het. Jy kan enige binêre getal gebruik (1, 01, 101101, ens.) tot `n heksadesimale getal, maar jy benodig vier syfers vir hierdie omskakeling (0101→5; 1100→C, ens.). In hierdie les begin ons met die binêre getal 1010 as voorbeeld.

1010
As die getal minder as 4 syfers is, plaas nulle voor dit om dit vier syfers te maak. So 01 word 0001.

Prent getiteld Skakel Binêr na Heksadesimale Stap 2 om

2. Skryf `n klein `1` bo die laaste getal. Elk van die vier getalle verteenwoordig `n getal uit die desimale getallestelsel. Die laaste syfer is dié van die eenhede. Die res van die getalle sal duideliker wees in die volgende stap. Skryf nou eers `n klein 1 bo die laaste getal.

1010

$10101$ $1010^{1}$

Let wel: dit is nie `n eksponensiëring nie - net `n spelling om aan te dui wat jy met `n sekere getal bedoel.

Prent getiteld Skakel Binêr na Heksadesimale Stap 3 om

3. Skryf `n klein `2` bo die derde syfer, `n `4` bo die tweede syfer en `n `8` bo die eerste syfer. Dit is die waardes van elke plek binne die binêre getal. Verduideliking: dit is omdat elke getal `n ander mag van 2 verteenwoordig. Die eerste is

23

$2^{3}$ , die tweede

22

$2^{2}$ , ens.

1010

$18 0^{4} 1^{2} 0^{1}$ $1^{8}0^{4}1^{2}0^{1}$

Prent getiteld Skakel Binêr na Heksadesimale Stap 4 om

4. Tel hoeveel van elke `plek` jy het. Gelukkig is hierdie omskakeling maklik as jy vier nommers het en weet wat hulle alles beteken. As jy `n een as die eerste syfer het, dan is dit `n agt as die desimale. As daar `n nul as die tweede syfer is, dan het jy nie `n vier nie. Die derde syfer staan vir die twee, en die eerste vir die 1. So in ons voorbeeld:

1010

18 0^{4} 1^{2} 0^{1}

$1^{8}0^{4}1^{2}0^{1}$

8 0 2 0

Prent getiteld Skakel Binêr na Heksadesimale Stap 5

5. Tel die vier getalle bymekaar. Sodra jy al die nuwe heksadesimale getalle het, voeg hulle net bymekaar.

1010

18 0^{4} 1^{2} 0^{1}

$1^{8}0^{4}1^{2}0^{1}$

8 0 2 0

8 + 0 + 2 + 0 = 10

$8+0+2+0=10$

Antwoord: Die binêre getal 1010 is a a in die heksadesimale getallestelsel.

Prent getiteld Skakel Binêr na Heksadesimale Stap 6 om

6. Verander enige nommer bo `9` na `n letter. Jy doen dit om nie verward te raak wanneer jy heksadesimale getalle lees nie (`is dit `n 1 en `n 5, of 15?`). Gelukkig is hierdie stelsel baie eenvoudig, want geen heksadesimale getal is groter as 15 nie. Begin met die alfabet by 10, dus:

10 = a

$10=A$

11 = B

$11=B$

12 = C

$12=C$

13 = d

$13=D$

14 = E

$14=E$

15 = f

$15=F$

Prent getiteld Skakel Binêr na Heksadesimale Stap 7

7. Probeer `n paar voorbeelde om beter te word met omskakeling. Vir die volgende voorbeelde is die antwoorde hieronder. Rollees af om die verduideliking en antwoorde te sien.

Skakel 1 om na `n heksadesimale.

Voeg nulle daarby om vier syfers te kry: 0001

Bepaal die waarde van elke plek:

08 0^{4} 0^{2} 1^{1}

$0^{8}0^{4}0^{2}1^{1}$

Tel die getalle bymekaar:

0 + 0 + 0 + 1 = 1

$0+0+0+1=1$

antwoord: 1

Skakel 0101 om na heksadesimale.

Voeg nulle by vir vier syfers: 0101

Bepaal die waarde van elke plek:

08 1^{4} 0^{2} 1^{1}

$0^{8}1^{4}0^{2}1^{1}$

Tel die getalle bymekaar:

0 + 4 + 0 + 1 = 5

$0+4+0+1=5$

antwoord: 5

Skakel 1110 om na heksadesimale.

Voeg nulle by vir vier syfers: 1110

Bepaal die waarde van elke plek:

18 1^{4} 1^{2} 0^{1}

$1^{8}1^{4}1^{2}0^{1}$

Tel die getalle bymekaar:

8 + 4 + 2 + 0 = 14

$8+4+2+0=14$

Antwoord: E

Skakel 0011 om na heksadesimale.

Voeg nulle by vir vier syfers: 0011

Bepaal die waarde van elke plek:

18 0^{4} 1^{2} 1^{1}

$1^{8}0^{4}1^{2}1^{1}$

Tel die getalle bymekaar:

8 + 0 + 2 + 1 = 11

$8+0+2+1=11$

Antwoord: B

Metode 2 van 2: Skakel langer binêre stringe om

Prent getiteld Skakel Binêr na Heksadesimale Stap 8 om

1. Verdeel die volgorde van binêre getalle in groepe van vier, begin van regs. Daar is vier binêre syfers in `n heksadesimale getal. So vir die omskakeling sal jy die reeks in groepe van vier moet verdeel, wat aan die regterkant begin. Byvoorbeeld:

Skakel om $11101100101001$ $11101100101001$ tot `n heksadesimale getal.
$11101100101001 = (11) (1011) (0010) (1001)$ $11101100101001=(11)(1011)(0010)(1001)$

Prent getiteld Skakel Binêr na Heksadesimale Stap 9 om

2. Plaas ekstra nulle voor die eerste nommer as dit nie vier syfers is nie. Die nulle sal nie die omskakeling beïnvloed nie, maar dit maak dit makliker om te visualiseer. Onthou dat julle almal groepe binêre getalle met vier syfers maak.

Skakel om

11101100101001

$11101100101001$ tot `n heksadesimale getal.

11101100101001 = (11) (1011) (0010) (1001)

$11101100101001=(11)(1011)(0010)(1001)$

(11) (1011) (0010) (1001) =

$(11)(1011)(0010)(1001)=$ $(0011) (1011) (0010) (1001)$ $(0011)(1011)(0010)(1001)$

Prent getiteld Skakel Binêr na Heksadesimale Stap 10 om

3. Skakel een groep op `n slag om. Jy sal elke binêre groep individueel moet omskakel, plaas dit dus apart op `n stuk papier om dit makliker te maak. Skakel alle binêre getalle om na heksadesimale vorm. In ons voorbeeld:

0011 = 0 + 0 + 2 + 1 = 3

$0011=0+0+2+1=3$

1011 = 8 + 0 + 2 + 1 = 11 = B

$1011=8+0+2+1=11=B$

0010 = 0 + 0 + 2 + 0 = 2

$0010=0+0+2+0=2$

1001 = 8 + 0 + 0 + 1 = 9

$1001=8+0+0+1=9$

Prent getiteld Skakel Binêr na Heksadesimale Stap 11 om

4. Plaas hierdie getalle langs mekaar vir die volle heksadesimale getal. Sodra jy alle groepe van vier syfers na heksadesimale omgeskakel het, plaas hulle eenvoudig een na die ander vir die finale antwoord. Dus, volgens die voorbeeld hierbo:

(0011) (1011) (0010) (1001)

3 B 2 9

$11101100101001 = 3 B 29$ $11101100101001=3B29$

5. Memoriseer of hersien `n omskakelingstabel om seker te maak dat jy hulle almal korrek omgeskakel het. Daar is slegs 16 moontlike kombinasies van vier binêre syfers. As jy dus nie elke binêre groep afsonderlik wil bereken nie, kan jy die volgende omskakelingstabel gebruik.

Binêre	Heksadesimale
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	a
1011	B
1100	C
1101	d
1110	E
1111	f

Wenke

Binêre getalle het basisse van twee (daar is net twee getalle; 1 en 0). Heksadesimale het basis sestien. Verstaan jy hoekom jy vier binêre syfers nodig het vir die omskakeling na heksadesimale? Dit is omdat jy vier afsonderlike twee nodig het, want $24 = 16$ $2^{4}=16$ .

Waarskuwings

As jy `n heksadesimale ekwivalent van `n binêre adres gevind het en jy doen dit verkeerd, sal die resultate in die heksadesimale adresinvoer nie meer korrek wees nie.