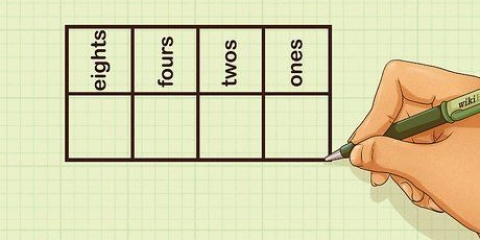
11 > 1, dus 11 "pas nie" 1. Skryf `n 0 as die eerste syfer van die kwosiënt (bo die eerste syfer van die dividend). 
Bring die volgende syfer van die dividend af. 11 > 10. Skryf `n 0 in die kwosiënt. Bring die volgende nommer af. 11 < 101. Skryf `n 1 in die kwosiënt. 
Skryf die deler onder die dividend neer. Hier skryf ons dit as 11 onder die eerste drie syfers (101) van die dividend. Bereken 101 - 11 vir die res, 10. Hersien hoe om binêre getalle af te trek as jy nie onthou nie. 
Skryf 11 onder 100 en trek hierdie getalle af om 1 te kry. Bring die laaste syfer van die dividend af en jy sal 11 as antwoord kry. 11 = 11, so jy skryf 1 as die laaste syfer van die kwosiënt (die antwoord). Daar is geen res nie, so die taak is voltooi. Die antwoord is 00111, of eenvoudiger, 111. 
Die verdeling van binêre getalle lei dikwels tot herhaalde getalle na die desimale punt, meer dikwels as dié wat met desimale notasie voorkom. Hierna word met die meer algemene term verwys "radiks punt" wat jy in elke getallestelsel teëkom, want jy het die "desimale punt" word slegs binne die desimale stelsel aangetref. 

Vind die komplement van die ene van die tweede term, trek elke syfer van 1 af. Jy kan dit maklik met binêre getalle doen deur elke 1 tot 0 en elke 0 op 1 te stel. In ons voorbeeld is 011 gelyk aan 100. Voeg 1 by die resultaat: 100 + 1 = 101. Dit word die 2`s-komplement genoem. Ons gaan nou `n minussom as `n optelsom beskou. Die essensie is dat ons die probleem beskou asof ons `n negatiewe getal optel in plaas van `n positiewe getal af te trek, nadat die prosedure voltooi is. Voeg die resultaat by die eerste kwartaal. Los die som op: 111 + 101 = 1100. Laat die eerste syfer weg (dra syfer). Verwyder die eerste syfer van jou antwoord om die finale resultaat te kry. 1100 → 100. 

2 se komplement van 000101 = 111010 + 1 = 111011 100011 + 111011 = 1011110 Laat die eerste syfer (die dra) weg → 011110 

011110 + 111011 = 1011001 → 011001 (kwosiënt 1+1=10) 011001 + 111011 = 1010100 → 010100 (kwosiënt 10+1=11) 010100 + 111011 = 1001111 → 001111 (11+1=100) 001111 + 111011 = 1001010 → 001010 (100+1=101) 001010 + 111011 = 10000101 → 0000101 (101+1=110) 0000101 + 111011 = 1000000 → 000000 (110+1=111) 0 is minder as 101, so nou kan ons stop. Die kwosiënt 111 is die antwoord op die subprobleem. Die res is die finale resultaat van ons minsum, in hierdie geval 0 (geen rus).
Verdeling van binêre getalle
Die verdeling van binêre getalle kan opgelos word deur langdeling te gebruik, `n gerieflike metode om jouself die prosedure te leer of om `n eenvoudige rekenaarprogram te skryf. Alternatiewelik bied die komplementmetode van herhaalde aftrekking `n benadering waarmee jy dalk nie vertroud is nie, hoewel dit nie regtig algemeen in programmering gebruik word nie. Masjientale gebruik gewoonlik `n skattingsalgoritme vir groter doeltreffendheid, maar dit word nie hier beskryf nie.
Trappe
Metode 1 van 2: Gebruik langdeling

1. Gaan weer oor desimale langdeling. As dit `n rukkie is sedert jy langdeling met gereelde desimale (basis 10) getalle gedoen het, hersien die basis daarvan vir die probleem 172 ÷ 4. Andersins, slaan dit oor en gaan na die volgende stap om hierdie prosedure vir binêre getalle te leer.
- Dit dividend word gedeel deur die deler, en die antwoord is dit kwosiënt.
- Vergelyk die deler met die eerste syfer in die dividend. As die deler die grootste getal is, hou aan om syfers by die dividend by te voeg totdat die deler die kleinste getal is. (As `n voorbeeld, wanneer ons 172 ÷ 4 bereken, vergelyk ons 4 en 1, ons vind dat 4 > 1, en vergelyk dan 4 met 17.)
- Skryf die eerste syfer van die kwosiënt bo die laaste syfer van die dividend wat vir vergelyking gebruik word. Nadat ons 4 en 17 vergelyk het, let ons daarop dat 4 vier keer in 17 gaan, dus skryf ons 4 as die eerste syfer van ons kwosiënt, bo 7.
- Vermenigvuldig en trek af om die res te vind. Vermenigvuldig die kwosiënt met die deler, in hierdie geval 4 x 4 = 16. Skryf die 16 onder die 17, en doen dan 17 - 16 vir die res, 1.
- Herhaal. Weereens vergelyk ons die deler 4 met die volgende syfer, 1, ons let op dat 4 > 1, en "bring" ons skuif die volgende syfer van die dividend af om eerder 4 met 12 te vergelyk. 4 gaan drie keer in 12 met geen res nie, dus kan ons 3 skryf as die volgende syfer van die kwosiënt. Die antwoord is 43.

2. Skep `n binêre langafdeling-opstelling. Gestel ons gebruik as voorbeeld 10101 ÷ 11. Skryf dit as lang deling, met 10101 as die dividend en 11 as die deler. Los spasie bo dit om die kwosiënt te skryf, en skryf jou berekeninge daaronder neer.

3. Vergelyk die deler met die eerste syfer van die dividend. Dit werk op dieselfde manier as desimale langdeling, maar is eintlik baie makliker in binêre vorm. Óf jy kan nie die getal deur die deler (0) deel nie, óf die deler pas een keer in (1):

4. Neem nou die volgende nommer en herhaal totdat jy 1 kry. Hier is die volgende paar stappe uit ons voorbeeld:

5. Bepaal die res. soos in desimale langdeling, vermenigvuldig ons die syfer wat ons sopas gevind het (1) met die deler (11), en skryf die resultaat onder ons dividend op `n lyn met die syfer wat ons pas bereken het. In binêre vorm kan ons dit vinniger doen, want 1 x die deler is altyd gelyk aan die deler:

6. Hou aan totdat die probleem opgelos is. Bring die volgende syfer van die handelaar na die res hieronder om 100 te kry. Omdat 11 < 100 skryf jy `n 1 as die volgende syfer van die kwosiënt. Gaan voort om die probleem uit te werk soos voorheen:

7. Voeg `n radixpunt by indien nodig. Soms is die resultaat nie `n heelgetal nie. As jy nog `n oorblyfsel het nadat jy die laaste syfer gebruik het, voeg `n by ".0" aan die dividend en a "." na jou kwosiënt sodat jy nog een nommer kan afbring en aanbeweeg. Hou aan om dit te doen totdat jy die verlangde akkuraatheid bereik, rond dan jou antwoord af. Op papier kan jy afrond deur die 0 weg te laat of, as die laaste syfer `n 1 is, dit aftrek en 1 by die laaste syfer tel. Wanneer jy programmeer, gebruik een van die standaard afrondingsalgoritmes om foute te vermy wanneer omgeskakel word tussen binêre en desimale getalle.
Metode 2 van 2: Gebruik die komplementmetode

1. Verstaan die basiese idee. Een manier om verdelings op te los - vir enige basis - is om aan te hou om die deler van die dividend af te trek, dan die res, om te bereken hoeveel keer jy dit kan aanhou doen voordat jy by `n negatiewe getal uitkom. Hier is `n voorbeeld vir die basis 10, die probleem 26 ÷ 7:
- 26 - 7 = 19 (1 tye afgetrek)
- 19 - 7 = 12 (2 tye afgetrek)
- 12 - 7 = 5 (3 tye afgetrek)
- 5 - 7 = -2. Negatiewe getal, so weer op. Die antwoord is 3 met `n res van 5. Let daarop dat hierdie metode nie desimale syfers in ag neem nie.

2. Leer om af te trek deur komplemente te gebruik. Alhoewel u bogenoemde metode maklik op binêre getalle kan toepas, kan ons ook `n meer doeltreffende metode gebruik, wat u tyd kan bespaar wanneer u binêre verdelings programmeer. Dit word die binêre komplementmetode genoem. Hier is die basiese beginsels, waar ons 111 - 011 bereken (maak seker dat beide getalle dieselfde lengte is):

3. Kombineer die twee konsepte hierbo. Nou weet jy hoe die aftrekmetode vir die oplos van delings werk, en die 2`s komplementmetode om die somme van minusse op te los. Jy kan die twee in een metode kombineer om deelprobleme op te los, deur die stappe hieronder te gebruik. As jy wil, kan jy self probeer uitvind voordat jy voortgaan.

4. Trek die deler van die dividend af deur die 2-komplement by te tel. Kom ons werk die volgende probleem uit: 100011 ÷ 000101. Die eerste stap is om 100011 - 000101 op te los, deur die 2 se komplementmetode te gebruik, sodat dit `n som word:

5. Voeg 1 by die kwosiënt. In `n rekenaarprogram is dit die punt waar jy die kwosiënt met 1 verhoog. Maak op papier `n nota in `n hoek iewers, waar dit nie die res van jou werk sal mors nie. Ons het nou een keer suksesvol `n minsum gedoen, so die kwosiënt tot dusver is 1.

6. Herhaal deur die deler van die res af te trek. Die resultaat van ons laaste berekening is die res wat een keer na die deler oorgebly het "ingegaan". Gaan voort met die optel van die deler se 2-komplement en trek die dra af. Voeg elke keer 1 by die kwosiënt, en gaan voort totdat jy `n res kry wat gelyk is aan jou kleiner deler:
Wenke
- Die inkrement, afname of stapelinstruksies moet oorweeg word voordat `n binêre berekening op `n stel masjienstellings toegepas word.
- Die 2 se komplementmetode vir aftrekking werk nie as die getalle uit `n ander aantal syfers bestaan nie. Voeg ekstra nulle by die kleiner getal om dit op te los.
- Ignoreer die getekende syfer in getekende binêre getalle voordat jy die berekening doen, behalwe wanneer jy probeer uitvind of `n antwoord positief of negatief is.
Artikels oor die onderwerp "Verdeling van binêre getalle"
Оцените, пожалуйста статью
Gewilde