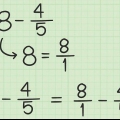Trek getalle af

Inhoud

Trappe
Wenke
Waarskuwings

Aftrekkings is daardie somme waar jy twee getalle van mekaar aftrek. Dit is redelik eenvoudig as jy heelgetalle van mekaar wil aftrek, maar word `n bietjie meer ingewikkeld as jy met breuke of desimale werk. Sodra jy aftrekking bemeester het, kan jy aanbeweeg na die meer ingewikkelde wiskundige konsepte en optel, vermenigvuldig en deel getalle sal baie makliker wees.

Trappe

Metode 1 van 6: Trek groot heelgetalle af deur te leen

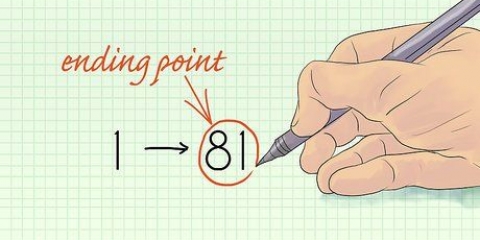
1. Skryf die groter getal neer. Gestel jy werk met die som 32 - 17. Skryf eers 32 neer.

2. Skryf die kleiner getal direk onder dit neer. Maak seker dat die tiene en ene netjies in lyn is sodat die 3 in "32" direk bo 1 duim "17" staat, en die 2 in "32" direk bokant die "7" op 17.

3. Trek die onderste getal van bo af. Dit kan `n bietjie moeilik raak as die onderste getal groter is as die boonste een. In hierdie geval is 7 groter as 2. Hier is wat om te doen:

jy sal moet "te leen" van die 3 in "32" om die 2 tot 12 te maak.

Kruis die 3 van "32" en maak dit `n 2, maak dan die eenheid 2 `n 12.

Nou het jy 12 – 7 = 5. Skryf `n 5 onder die eenhede kolom.

4. Trek die tien in die onderste getal af van die tien in die boonste getal. Moenie vergeet dat die 3 van 32 `n 2 geword het nie. Trek nou die 1 uit 17 af van die 2 daarbo, dus 2-1= 1. Skryf 1 onder die tiene-kolom. As alles goed is, het jy nou 15 as `n antwoord, dus 32 - 17 = 15.

5. Gaan jou werk na. As jy seker wil maak dat jy die berekening korrek gedoen het, hoef jy net die antwoord by die kleinste getal te voeg om die grootste getal terug te kry. So om te kontroleer: 15 + 17 = 32, so jy het dit reg gedoen. Uitstekend!

Metode 2 van 6: Trek klein heelgetalle af

1. Bepaal watter getal groter is. `n Oefening soos 15 - 9 vereis `n ander benadering as 2 - 30.

In die som 15 - 9 is die eerste getal, 15, die grootste.
In die som 2 - 30, die tweede getal, is 30 die grootste.

2. Besluit of jou antwoord positief of negatief moet wees. As die eerste getal die grootste is, dan is die antwoord positief. As die tweede getal die grootste is, is die antwoord negatief.

Dus in die eerste som, 15 - 9, word die antwoord positief, want 15 is groter as 9.

Dus in die tweede som, 2 - 30, word die antwoord negatief, want 2 is minder as 30.

3. Vind die verskil tussen die twee getalle. Om twee getalle af te trek, bereken die verskil tussen hulle.

Vir die probleem 15 - 9, neem 15 munte. Verwyder 9 en tel hoeveel oor is (6). Dus, 15 - 9 = 6. Of gebruik `n getallelyn en trek die nommers 1 tot 15 langs die lyn, trek dan 9 deur van 15 af om by 6 te kom.

Met die som 2 – 30 is dit makliker om die getalle om te draai en die antwoord negatief te maak. Dus, 30 - 2 = 28, en daarmee is 2 - 30 -28.

Metode 3 van 6: Trek desimale af

1. Skryf die groter getal bo die kleiner getal sodat die desimale in lyn is. Gestel jy het die volgende probleem: 10.5 - 8.3. Skryf die 10.5 bo 8.3 op so `n manier dat die kommas bo mekaar is.

As jy `n probleem het waar een getal meer desimale plekke as die ander het, vul die leë spasie met nulle. Byvoorbeeld, as jy die probleem 5.32 - 4.2 het, kan jy dit herskryf as 5.32 = 4.20. Dit verander nie die waarde van `n getal nie, maar jy maak seker dat beide getalle makliker van mekaar afgetrek kan word.

2. Trek die tiendes van mekaar af. Aftrekking van hierdie getalle is dieselfde as met die heelgetalle, behalwe dat jy moet let op die desimale punt, belyn en by die antwoord ingesluit. In hierdie geval moet jy 3 van 5 aftrek. 5 - 3 = 2, so jy skryf `n 2 onder die 3 in 8.3.

Moenie vergeet om die desimale punt (die komma) by die antwoord in te sluit nie. Dit lyk nou so: ,2.

3. Trek nou die eenhede van mekaar af. Trek nou 8 van 0 af. Leen `n dosyn van die 1 (langs die 0) om 10 te maak, trek nou 8 van 10 af. Jy kan ook dadelik die som 10 – 8 = 2 bereken, sonder die tussenstap van leen, want die onderste getal het nie `n tien. Skryf die antwoord onder 8.

4. Die finale antwoord sal dus 2.2 wees.

5. Gaan jou werk na. As jy seker wil maak dat jy die berekening korrek gedoen het, hoef jy net die antwoord by die kleinste getal te voeg om die grootste getal terug te kry. 2.2 + 8.3 = 10.5 so jy is gereed.

Metode 4 van 6: Trek breuke af

1. Sit die tellers en die noemers saam. Gestel jy werk met die probleem 13/10 - 3/5. Skryf hierdie probleem so dat beide tellers, 13 en 3, en beide noemers, 10 en 5, langs mekaar is, geskei deur `n minusteken. Dit gee jou `n beter oorsig van die probleem en maak dit makliker om `n oplossing te vind.

2. Vind die kleinste gemene veelvoud. Dit is die kleinste veelvoud van twee getalle. Die LCF van 10 en 5 in hierdie voorbeeld is 10.

Let daarop dat die lcm van twee getalle nie altyd een van die twee getalle is nie. Byvoorbeeld, by 3 en 2 is die LCF 6, want daar is geen getal minder as 6 wat `n veelvoud van elk van die getalle is nie.

3. Skryf die breuke oor met dieselfde noemers. Die breuk 13/10 kan onveranderd bly omdat die noemer nie verander het nie, maar die breuk 3/5 word gelyk aan 6/10 omdat die noemer twee keer in die gemene veelvoud van 10 gaan. Nou het jy albei breuke gelyk gemaak. 3/5 is gelyk aan 6/10, maar met die verskil dat dit nou nie meer `n probleem is om beide breuke van mekaar af te trek nie.

Die nuwe taak sal dus wees: 13/10 - 6/10.

4. Trek beide tellers van mekaar af. Dus 13 - 6 = 7. Moenie die noemers aftrek nie.

5. Plaas die nuwe teller bo die nuwe noemer (die voorheen berekende LCF) vir die finale antwoord. Die nuwe teller is 7 en die noemer van beide breuke is 10. Die finale antwoord is dus 7/10.

6. Gaan jou werk na. As jy seker wil maak dat jy die berekening korrek gedoen het, hoef jy net die antwoord by die kleinste getal te voeg om die grootste getal terug te kry. So om te kontroleer: 7/10 + 6/10 = 13/10. Jy is nou gereed.

Metode 5 van 6: Trek `n breuk van `n heelgetal af

1. Skryf die opdrag. Gestel ons het die volgende probleem: 5 - 3/4. Let hierop.

2. Skakel die heelgetal om in `n breuk met dieselfde noemer as die gegewe breuk. Maak `n breuk van die 5 met die noemer 4. Oorweeg eers dat 5 gelyk is aan die breuk 5/1. Dan vermenigvuldig jy beide die teller en noemer van die nuwe breuk met 4 om twee breuke met dieselfde noemer te kry. Dit hou die waarde van die breuk dieselfde, maar met verskillende getalle. Dus, 5/1 x 4/4 = 20/4.

3. Herskryf die opdrag. Dit kan nou geskryf word as: 20/4 - 3/4.

4. Trek die tellers van die breuke af en hou die breuke gelyk. Dus, 20 - 3 = 17. Die finale teller word dus 17 en die noemer is 4.

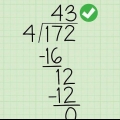
5. Die antwoord op die probleem is dus 17/4. Om hierdie onbehoorlike breuk in `n saamgestelde breuk om te skakel, deel 17 deur 4 om die getal 4 te kry met `n res van 1. Die antwoord lyk dan soos volg: 4 1/4.

Metode 6 van 6: Aftrek van veranderlikes

1. Skryf die opdrag. Gestel jy werk aan die volgende probleem: 3x - 5x + 2y - z - (2x + 2x + y). Skryf die eerste vergelyking bo die tweede.

2. Trek alle soortgelyke terme van mekaar af. Wanneer jy met veranderlikes werk, kan jy slegs terme met dieselfde veranderlike aftrek en met dieselfde krag. Dit beteken jy kan 4x -7x doen, maar nie 4x -7x nie. So jy kan hierdie taak soos volg verdeel:

3x - 2x = x

-5x - 2x = -7x

2j - j = j

-z - 0 = -z

3. Gee jou finale antwoord. Noudat jy alle gelyke terme afgetrek het, kan jy dadelik jou finale antwoord gee. Hier is die antwoord:

3x - 5x + 2y - z - (2x + 2x + y) = x - 7x + y - z

Wenke

Breek groter getalle in kleiner stukke op. Neem: 63 - 25.Niemand sê jy moet al 25 gelyktydig aftrek nie. Jy kan eers 3 aftrek om 60 te kry; trek dan 20 af om 40 te kry en dan die laaste 2. Resultaat: 38. En nou hoef jy nie te leen nie.