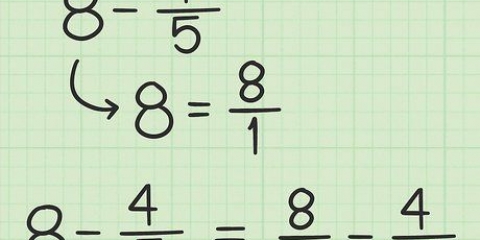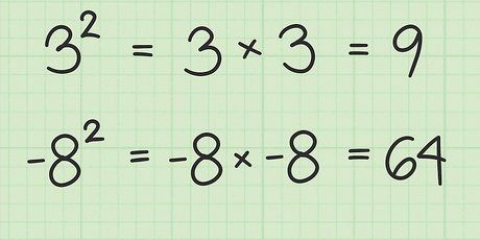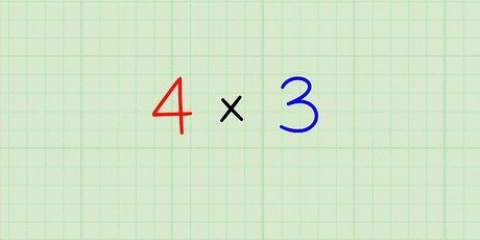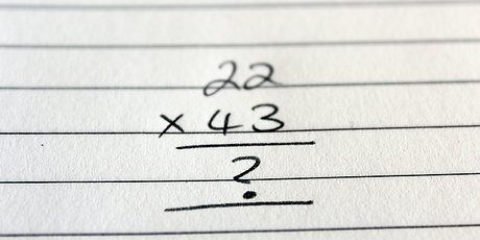Jou wiskundeboek kan hierdie punt dit noem punt van oorsprong, want dit is die punt waar die getalle vandaan kom ontstaan, of begin. 
Moenie te veel bekommerd wees oor perfekte spasiëring nie - solank dit so lyk, sal die getallelyn goed werk. 
Die voorbeeld is `n genommerde lyn van -6 tot 6. 
Breuke soos 1/2 is deel van `n getal, nie heelgetalle nie. Net so met `n desimaal soos 0,25; desimale is nie heelgetalle nie. 
Vind jy dit `n bietjie te maklik? Jy sal nie onbekend wees met optel nie en jy kan 1 + 2 uit jou kop oplos. Wonderlik: as jy reeds die antwoord ken, is dit makliker om te verstaan hoe die getallelyn werk. Dan kan jy `n getallelyn begin gebruik vir meer ingewikkelde probleme, of om vir wiskunde en algebra voor te berei. 




As voorbeeld neem ons die som 1 + -4. Op `n getallelyn begin ons by 1, skuif 4 spasies na links en eindig by -3. 

Neem as voorbeeld -4. As jy -4 by 1 bytel, verminder jy 1 met 4. Of op die wiskundige manier:
1 + (-4) = 1 - 4
Ons skryf dit op `n getallelyn, en plaas ons vinger op die 1, dan skuif jy 4 spasies na links (met ander woorde, voeg by met -4). Aangesien dit `n vergelyking is, is links gelyk aan regs - so die omgekeerde geld ook:
1 - 4 = 1 + (-4)

Op `n getallelyn begin ons by 5, verminder met 8 en eindig by -3. Dit word opgemerk as
5 - 8 = -3



Ons weet reeds dat 5 - 8 = -3, dus laat ons 5 - 8 uit ons vergelyking weglaat en `n -3 daarin plaas:
5 - (8 - 1) = 5 - 7 = -3 + 1
Ons weet reeds wat 5 - (8 - 1) is — jy skuif `n merker minder as 5 - 8. Ons vergelyking wys dat 5 - 8 = -3, en 1 stap minder is so -2. Nou kan ons vergelyking geskryf word as:
-3 - (-1) = -3 + 1



Onder die twee nommers aan die regterkant, 3 en 1, skryf die antwoord van die optelling van beide getalle neer: 4 Dus. 
Die antwoord wat jy kry is, as jy dit reg gedoen het: 9964. As jy `n fout gemaak het, kontroleer jou effek. 

As jy wil weet hoe dit werk, dink aan wat die verdeling van die 1 en 2 beteken. Jy verdeel eintlik 12 in 10 en 2. Jy kan die 10 heeltemal bokant die getalle skryf as jy wil, waarna jy sal sien dat die 1 ooreenstem met die 5 en die 3, soos dit moet. 

Jy kan effens moeiliker probleme probeer, soos 974+568. Onthou dat elke keer as jy `n tweesyfergetal kry, jy net die laat syfer met die antwoord en die eerste syfer bokant die volgende paar getalle (die volgende kolom) plaas. As die laaste som `n tweesyfer-antwoord het, kan jy albei by die antwoord onder die reël plaas. Kyk na die Wenke vir `n antwoord op die probleem 974+568 om jou eie antwoord na te gaan. 

Die antwoord moet wees: 4211. 

Trek die 2 van die boonste nommer deur en skryf `n 1 daar neer. Die 2 is direk aan die linkerkant van die 4. Trek die 4 deur en maak dit 14. Doen dit in `n klein spasie, sodat dit duidelik is aan watter getallepaar 14 behoort, en dus 14 – 8 aandui. Jy kan ook net `n 1 voor die 4 skryf, as daar genoeg spasie is. Wat jy sopas gedoen het, is dit "te leen" van `n 1 uit die kolom met tiene, of ook die tweede kolom aan die regterkant, sodat jy 10 tot 4 kan byvoeg. Dit sal jou 14 gee in die kolom met eenhede. 

Jou antwoord tot dusver behoort 06 om te wees. 

Maak seker dat die getalle reg is voordat jy dit vergelyk. 912 is nie groter as 5000, wat maklik is om te sien of die getalle korrek in lyn is, want die 5 is nie bo enigiets nie. Jy kan 1 of meer nulle voor die nommer plaas, as dit help. Skryf byvoorbeeld 912 as 0912 sodat dit dieselfde lengte as 5000 is. 

Die nuwe probleem om op te los is: 968.772 - 415.990 = - ? Kyk na die wenke om jou antwoord na te gaan. 

Gestel jy het 4 + -7. Maak dit `n minussom: 4 - 7 Keer die volgorde om en maak die som negatief: -(7 – 4) = -(3) = -3. As jy nie gewoond is daaraan om hakies in jou somme te gebruik nie, dink so daaroor: 4 - 7 word 7 - 4 en voeg `n minusteken by. So 7 - 4 = 3 en dan maak jy dit -3 om die korrekte antwoord op die som 4 - 7 te kry. 
-3 + -6 = -9 -15 + -5 = -20 Sien jy die patroon? Al wat jy hoef te doen is om die getalle bymekaar te tel asof hulle positief is en dan `n negatiewe teken daarby te voeg. -4 + -3 = -(4 + 3) = -7 
Dink aan `n negatiewe getal as gesteelde geld. as jy iets "ruk af", of van die gesteelde geld wegneem om dit terug te gee, dit is dieselfde as om geld aan daardie persoon te gee, of nie? Voorbeeld: 10 – -5 = 10 + 5 = 10 Voorbeeld: -1 – -2 = -1 + 2. Jy het reeds geleer hoe om dit op te los, in `n vroeëre stap, onthou? herlees "Leer hoe om `n negatiewe en `n positiewe getal by te tel" as jy nie weet nie. Hier is die volledige oplossing van die laaste voorbeeld: -1 – -2 = -1 + 2 = 2 + -1 = 2 – 1 = 1.
Tel en trek heelgetalle af
Inhoud
- Trappe
- Metode 1 van 5: Optelling en aftrekking van positiewe heelgetalle met `n getallelyn
- Metode 2 van 5: Optel en aftrek van negatiewe getalle op `n getallelyn
- Metode 3 van 5: Voeg groot positiewe heelgetalle by
- Metode 4 van 5: Trek groot positiewe heelgetalle af
- Metode 5 van 5: Optel en aftrek van negatiewe heelgetalle
- Wenke
Jy sou heelgetalle kan aan dink as die algemene getalle, soos 3, -12, 17, 0, 7000 of -582. Heelgetalle word ook so genoem omdat hulle nie in dele van getalle verdeel word nie, soos breuke en desimale. Lees hierdie artikel om alles te leer wat jy moet weet oor die optel en aftrek van heelgetalle, of spring reguit na `n area waarmee jy hulp nodig het.
Trappe
Metode 1 van 5: Optelling en aftrekking van positiewe heelgetalle met `n getallelyn

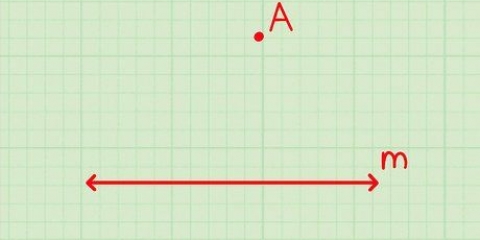
1. Wat is `n getallelyn. ’n Getallelyn verander om met getalle te werk in iets werklik en tasbaar wat jy jou kan voorstel. Deur merkers en jou verstand te gebruik, kan ons dit as `n soort sakrekenaar toepas om getalle op te tel en af te trek.

2. Trek `n basiese getallelyn. Trek `n reguit lyn. Plaas `n merk in die middel van die lyn. Skryf `n 0 of nul langs hierdie merk.

3. Trek twee punte, 1 aan elke kant van die nul. skryf -1 langs die merker aan die linkerkant en 1 aan die regterkant. Dit is die heelgetalle naaste aan nul.

4. Voeg meer getalle by die reël. Plaas meer merkers links van -1 en regs van 1. Soos volg: -2, -3, en -4 en aan die regterkant die merke 2, 3, en 4, ens. soveel as wat jy op die papier kan sit.

5. Verstaan wat positiewe en negatiewe heelgetalle is. `n Positiewe heelgetal, ook genoem a natuurlike getal, is `n heelgetal groter as nul. 1, 2, 3, 25, 99 en 2007 is almal positiewe heelgetalle. A negatief heelgetal is `n heelgetal kleiner as nul (soos -2, -4 en -88).

6. Los 1+2 op deur jou vinger op die merker gemerk 1 te plaas.

7. Doen die som 1+2 deur jou vinger 2 punte na regs te skuif. Tel die aantal merkers wat jy slaag. Het jy 2 punte gehad, stop. Die nommer waarna u vinger wys is die antwoord: 3.

8. Nog `n voorbeeld. Gestel ons wil weet wat 3 + 2 is. Begin by 3, beweeg na regs en Verhoog met 2. Ons eindig om 5. Jy skryf dit as 3 + 2 = 5.

9. Trek positiewe heelgetalle af deur links op die getallelyn te beweeg. As voorbeeld het ons die som 6 – 4. Ons begin by 6, skuif 4 merkers na links en eindig by 2. Jy skryf dit as 6 - 4 = 2.
Metode 2 van 5: Optel en aftrek van negatiewe getalle op `n getallelyn

1. Leer wat `n getallelyn is. As jy nie weet hoe om `n getallelyn te maak nie, gaan terug na Optel en aftrek positiewe getalle en lees dit weer.

2. Verstaan wat negatiewe getalle is. Positiewe getalle is aan die regterkant van die nul en negatiewe getalle aan die linkerkant van die getallelyn. Deur `n negatiewe getal by te voeg, beweeg jou vinger na links op die getallelyn.

3. Gebruik `n vergelyking om optel met `n negatiewe getal te verstaan. Let daarop dat -3, ons antwoord, dieselfde is as ons die som 1 – 4 uitwerk. 1 + (-4) en 4 - 1 is dieselfde. Ons kan dit ook skryf as `n vergelyking, `n wiskundige manier om te wys dat twee dinge gelyk is:
1 + (-4) = 1 - 4 = -3

4. In plaas daarvan om `n negatiewe getal by te tel, kan ons dit ook `n minussom maak met slegs positiewe getalle. Soos u uit ons eenvoudige vergelyking kon sien, kan ons twee maniere gaan - "voeg `n negatiewe getal by" of "trek `n positiewe getal af". Jy moes dit dalk leer sonder om te weet hoekom - hier is die rede.
Ons skryf dit op `n getallelyn, en plaas ons vinger op die 1, dan skuif jy 4 spasies na links (met ander woorde, voeg by met -4). Aangesien dit `n vergelyking is, is links gelyk aan regs - so die omgekeerde geld ook:

5. Verstaan hoe die aftrekking van negatiewe getalle op `n getallelyn werk. Op `n getallelyn is die aftrekking van `n negatief gelyk aan skuif na regs. Kom ons begin met 5 - 8.

6. Verminder die getal wat jy aftrek en kyk wat gebeur. Gestel die som word 5 -7. Nou skuif ons 1 plek minder na links op die getallelyn. Jy skryf dit as
5 - 7 = -2

7. Let daarop dat `n afname tot `n toename kan lei. In hierdie voorbeeld verminder ons die aantal plekke na links met 1. Ter vergelyking word dit:
5 - 7 = -2 = 5 - (8 - 1)

8. Verander `n minus in `n plus wanneer negatiewe getalle bygevoeg word. Deur die stap te gebruik "verander aftrekking na optelling", kan ons dit nou korter skryf as:
5 - (8 - 1) = 5 - 7 = 5 - 8 + 1 .

9. Skryf die aftrekking van negatiewe getalle as `n optelling. Let op wat aan die einde gebeur het - ons het bewys dat:
-3 + 1 = -3 - (-1)
Ons kan dit uitdruk as `n eenvoudige, meer algemene wiskundige reël:
eerste getal plus `n tweede getal = eerste getal minus negatiewe tweede getal)
Of, in eenvoudiger terme soos in wiskundeklas:
Verander twee minusse in een plus .
Ons kan dit uitdruk as `n eenvoudige, meer algemene wiskundige reël:
Of, in eenvoudiger terme soos in wiskundeklas:
Metode 3 van 5: Voeg groot positiewe heelgetalle by

1. Skryf die optelling 2503 + 7461 met een getal bo die ander. Plaas die getalle bo mekaar, sodat die 2 bo 7 is, die 5 bo 4 is, ens. In hierdie metode sal ons leer hoe om getalle by te voeg wat te groot is om te memoriseer of met `n getallelyn.
- Skryf `n + aan die linkerkant van die onderste nommer, en `n reël daaronder.

2. Begin om die twee nommers heel regs by te voeg. Dit lyk dalk vreemd om regs te begin omdat ons so gewoond is om getalle van links na regs te lees. Ons hou hierdie volgorde want anders sal ons nie die korrekte antwoord kry nie, soos u later sal sien.

3. Tel elke nommer op dieselfde manier by. Werk van links na regs, doen die volgende byvoegings: 0+6, 5+4, en 2+7. Skryf die antwoorde onder die getallepare neer.

4. Doen nou die som 857+135. Hier sien jy `n verskil met die vorige een, want 7+5 is gelyk aan 12, `n getal met 2 syfers. Maar jy kan nie meer as 1 syfer onder `n paar getalle plaas nie. Hou aan lees om te leer wat om te doen, en hoekom jy altyd regs in plaas van links moet begin.

5. Doen die som 7 + 5 en leer wat om met die antwoord te doen. 7+5=12, maar jy plaas net die 2 onder die lyn en die eerste syfer, 1, plaas jou hierbo die tweede paar getalle, 5+3.

6. Doen die som 1+5+3 om die volgende syfer van die antwoord te kry. Jy het nou 3 syfers om by te voeg, want jy het die 1 daarby gevoeg. Die antwoord is 9, so jou antwoord tot dusver is92.

7. Voltooi die opdrag soos gewoonlik. Hou aan om die somme van regs na links uit te werk totdat jy klaar is, voeg nog `n kolom by in hierdie geval. Jou finale antwoord is 992.
Metode 4 van 5: Trek groot positiewe heelgetalle af

1. Skryf die som 4713 - 502 met die eerste getal bo die tweede. Skryf dit so dat die 3 direk bo die 2 is, die 1 is bo die 0, die 7 is bo die 5 en die 4 is bo die leë spasie.
- Jy kan `n 0 onder 4 plaas as dit jou help om beide getalle in lyn te bring. `n Nul voor `n getal verander nie die waarde van daardie getal nie. `n Nul daarna doen, so moenie die nul daar plaas nie.

2. Trek elke onderste getal af van die getal direk bo dit, begin heel regs. Los die volgende probleme agtereenvolgens op: 3-2, 1-0, 7-5 en 4-0. Plaas die antwoorde direk onder die getallepaar waaraan dit behoort.

3. Doen nou die oefening 924 - 518 op dieselfde manier. Hierdie nommers is ewe lank, so jy kan hulle maklik in lyn bring. Hierdie oefening sal jou iets nuuts leer oor die aftrek van heelgetalle (hopelik).

4. Die eerste probleem, 4 - 8. Hierdie een is moeilik, want 4 is minder as 8, maar ons gaan nie negatiewe getalle gebruik nie. Hier is hoe om dit op te los:

5. Los nou probleem 14 - 8 op en skryf die antwoord onder die regterkolom neer. Jy behoort nou `n 6 heel links onder die lyn te sien.

6. Los die volgende kolom (links) op met die nuwe nommer (die 2 is deur `n 1 vervang). Dit word dus 1 - 1, wat gelyk is aan 0.

7. Voltooi die probleem deur die laaste kolom op te los. 9 - 5=4, so die antwoord is 406.

8. Nou gaan ons aan na `n probleem waar ons `n groter getal van `n kleiner getal aftrek. Gestel jy het 415.990 – 968.772 moet oplos. Jy skryf die tweede nommer onder die eerste, dan besef jy dat die onderste nommer groter is!

9. Skryf die kleiner getal onder die groter getal en plaas `n minusteken voor die antwoord. Elke keer as jy `n getal van `n kleiner getal aftrek, kry jy `n negatiewe getal as `n antwoord. Dit is die beste om die minusteken neer te skryf voordat jy die probleem oplos sodat jy nie vergeet nie.

10. Om die antwoord te vind, trek die klein getal van die groter getal af. Moenie die minusteken vergeet nie. Jou antwoord sal negatief wees, soos jy met die minusteken aangedui het. Probeer nie om `n groter getal van `n kleiner getal af te trek en dit dan negatief te maak; as gevolg hiervan sal jy nie die korrekte antwoord kry nie.
Metode 5 van 5: Optel en aftrek van negatiewe heelgetalle

1. Leer hoe om `n negatiewe en `n positiewe getal by te voeg. Om `n negatiewe heelgetal by te tel is dieselfde as om `n positiewe getal af te trek. Dit is makliker om te sien deur dit uit te toets met die getallelynmetode soos beskryf in `n ander afdeling, maar jy kan ook in woorde daaroor dink. `n Negatiewe getal is nie `n normale hoeveelheid nie; dit is minder as nul, en kan `n hoeveelheid voorstel wat weggeneem word. As jy hiervan hou "te verdryf" hoeveelheid tot `n gewone getal, dan maak jy dit kleiner.
- Voorbeeld: 10 + -3 = 10 - 3 = 7
- Voorbeeld: -12 + 18 = 18 + -12 = 18 – 12 = 6. Onthou dat jy altyd die volgorde van getalle bykomend kan verander, maar nie wanneer dit afgetrek word.

2. Leer wat om te doen wanneer dit `n minussom met die kleinste getal word. Soms kan dit gebeur dat die omskakeling van `n som na `n minus som resultate soos 4 – 7 gee. As dit gebeur, draai die getalle om en maak die antwoord negatief.

3. Leer hoe om twee negatiewe heelgetalle by te voeg. Twee negatiewe getalle wat bymekaar getel word, maak altyd die antwoord negatief en groter. Niks positiefs word daarby gevoeg nie, so jy sit altyd met iets nog verder van nul af. Dit is maklik om die antwoord te vind:

4. Leer hoe om `n negatiewe heelgetal af te trek. Soos met die plussomme, kan jy dit herskryf sodat jy net met positiewe getalle te doen het. As jy `n negatiewe getal aftrek, dan "vat jy iets weg" deur "iets wat weggeneem word", wat dieselfde is as om `n positiewe getal by te tel.
Wenke
- Jy is waarskynlik gewoond daaraan om lang getalle soos 2 te skryf.521.301. In baie lande is dit algemeen om `n komma in plaas van `n punt te gebruik, of omgekeerd (vir desimale). Moenie dat dit jou verwar wanneer jy op die internet soek vir inligting oor hierdie onderwerp nie. Hou by wat jy op skool hieroor leer.
- Skep verskillende getallelyne vir verskillende getalle. Dit is nie `n reël dat getallelyne altyd oor heelgetalle gaan nie. Dit kan ook omtrent tiene of breuke wees. Behalwe dat elke spasie nou iets anders verteenwoordig, kan jy steeds die getallelyn vir optel en aftrek op dieselfde manier gebruik. Probeer dit.
- As jy die ekstra probleem in die groot getalle-afdeling probeer het, is hier die antwoorde: 974 + 568 = 1542. Die antwoord op die som 415.990 – 968.772 is -552.782.
Artikels oor die onderwerp "Tel en trek heelgetalle af"
Оцените, пожалуйста статью
Gewilde