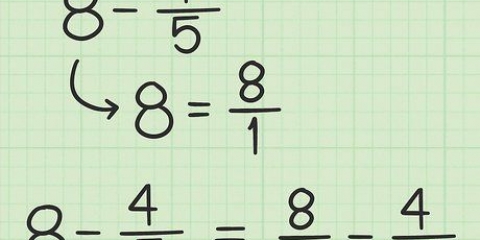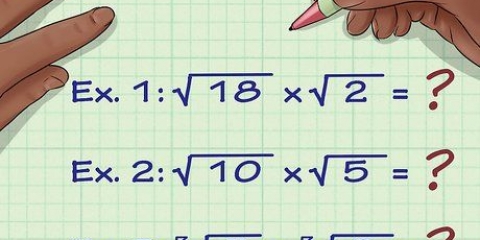Tel en trek vierkantswortels af: 9 stappe (met prente)

Inhoud

Trappe
- Deel 1 van 2: Bemeestering van die basiese beginsels
- Deel 2 van 2: Meer oefening
Wenke
Waarskuwings

Om vierkantswortels op te tel en af te trek, moet jy vierkantswortels met dieselfde wortel kombineer. Dit beteken dat jy 2√3 tot 4√3 kan optel (of aftrek van) maar jy kan nie 2√3 en 2√5 optel nie. Daar is baie gevalle waar jy die getal onder die radikaal kan vereenvoudig om soortgelyke terme te kan kombineer en vierkantswortels vrylik kan optel en aftrek.

Trappe

Deel 1 van 2: Bemeestering van die basiese beginsels

Prent getiteld Tel en trek vierkantswortels af Stap 1

1. Vereenvoudig die terme onder die radikale indien moontlik. Om die terme onder die radikale te vereenvoudig, probeer om hulle in ten minste een perfekte vierkant te verreken, soos 25 (5 x 5) of 9 (3 x 3). Sodra jy dit gedoen het, kan jy die vierkantswortel van die perfekte vierkant neem en dit buite die radikale plaas, en die oorblywende faktor onder die radikaal laat. In hierdie voorbeeld begin ons by die probleem 6√50 - 2√8 + 5√12. Die getalle buite die radikale is die koëffisiënte en die nommers daaronder noem ons die wortelgetalle. Hier is hoe om die terme te vereenvoudig:

6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Jy het `50` in `25 x 2` opgelos en dan `5` buite die wortel geplaas (die wortel van `25`), waarna `2` onder die radikaal bly. Dan vermenigvuldig jy `5` met `6`, die getal wat reeds buite die radikaal was, en jy kry 30 as die nuwe koëffisiënt.
2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Hier het jy `8` in `4 x 2` in berekening gebring en dan die vierkantswortel van 4 afgetrek sodat jy met `2` buite die radikaal gelaat word, en `n `2` onder die radikaal. Dan vermenigvuldig jy `2` met `2`, die getal wat reeds buite die radikaal was, en jy kry 4 as die nuwe koëffisiënt.
5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Hier het jy `12` in `4 x 3` in berekening gebring en dan die vierkantswortel van 4 afgetrek sodat jy met `2` buite die radikaal gelaat word, en `n `3` onder die radikaal. Dan vermenigvuldig jy `2` met `5`, die getal wat reeds buite die radikaal was, en jy kry 10 as die nuwe koëffisiënt.

Prent getiteld Tel en trek vierkantswortels af Stap 2

2. Omkring enige terme met ooreenstemmende wortelgetalle. Sodra jy die wortelgetalle van die gegewe terme vereenvoudig het, bly jy met die volgende vergelyking: 30√2 - 4√2 + 10√3. Aangesien jy net soos wortels kan optel of aftrek, moet jy daardie terme met dieselfde wortel omkring, in hierdie voorbeeld: 30√2 en 4√2. Jy kan dit vergelyk met die optel of aftrek van breuke, waar jy slegs die terme kan optel of aftrek as die noemers gelyk is.

Prent getiteld Tel en trek vierkantswortels af Stap 3

3. As jy met `n langer vergelyking werk en daar is veelvuldige pare ooreenstemmende wortelgetalle, kan jy die eerste paar omkring, die tweede onderstreep, die derde asterisk, ensovoorts. Om soortgelyke terme in volgorde te plaas, sal dit vir jou makliker maak om die oplossing te visualiseer.

Prent getiteld Tel en trek vierkantswortels af Stap 4

4. Bereken die som van die koëffisiënte van die terme met gelyke wortels. Nou al wat jy hoef te doen is om die som van die koëffisiënte van die terme met gelyke wortels te bereken, en ignoreer die ander terme van die vergelyking. Die wortelgetalle bly onveranderd. Die idee is dat jy aandui hoeveel van daardie tipe wortelgetal daar in totaal is. Die terme wat nie ooreenstem nie, kan bly soos hulle is. Hier is wat jy doen:

30√2 - 4√2 + 10√3 =

(30 - 4)√2 + 10√3 =

26√2 + 10√3

Deel 2 van 2: Meer oefening

Prent getiteld Tel en trek vierkantswortels af Stap 5

1. Doen voorbeeld 1. In hierdie voorbeeld voeg jy die volgende vierkantswortels by: √(45) + 4√5. Jy moet die volgende doen:

Vereenvoudig (45). Eers kan jy dit so losmaak √(9 x 5).
Dan neem jy die vierkantswortel van nege en jy kry `3`, wat jy dan buite die vierkantswortel plaas. Dus, √(45) = 3√5.
Voeg nou die koëffisiënte van die twee terme met bypassende wortels by om jou antwoord te kry. 3√5 + 4√5 = 7√5

Prent getiteld Tel en trek vierkantswortels af Stap 6

2. Doen voorbeeld 2. Die volgende voorbeeld is hierdie opdrag: 6√(40) - 3√(10) + √5. Jy moet die volgende doen om dit reg te stel:

Vereenvoudig 6√(40). Eerstens kan jy `40` in `4 x 10` oplos, en jy kry 6√(40) = 6√(4×10).

Dan bereken jy `2` uit die vierkant `4`, en jy vermenigvuldig dit met die huidige koëffisiënt. Nou het jy 6√(4×10) = (6 x 2)√10.

Vermenigvuldig die twee koëffisiënte en jy kry 12√10`.`

Die taak lui nou soos volg: 12√10 - 3√(10) + √5. Aangesien die eerste twee terme dieselfde wortel het, kan jy die tweede term van die eerste aftrek en die derde laat soos dit is.

jy is nou lief (12-3)√10 + √5 oor, wat vereenvoudig kan word om 9√10 + √5.

3. Doen voorbeeld 3. Hierdie voorbeeld gaan soos volg: 9√5 -2√3 - 4√5. Geen van die wortels bevat `n vierkant nie, so geen vereenvoudiging is moontlik nie. Die eerste en derde terme het gelyke wortels, so hul koëffisiënte kan afgetrek word (9 - 4). Die wortelgetal bly dieselfde. Die oorblywende terme is nie gelyk nie, dus kan die probleem vereenvoudig word5√5 - 2√3`.`

Prent getiteld Tel en trek vierkantswortels af Stap 7

Prent getiteld Voeg vierkantswortels by en aftrek Stap 8

4. Doen voorbeeld 4. Gestel jy het met die volgende probleem te doen: √9 + √4 - 3√2 Jy moet nou die volgende doen:

Omdat √9 gelyk is √(3x3), kan jy dit vereenvoudig: √9 word 3.

Omdat √4 gelyk is √(2x2), kan jy dit vereenvoudig: √4 word 2.

Nou die som 3 + 2 = 5.

Omdat 5 en 3√2 is nie gelyke terme nie, daar is niks meer om nou te doen nie. Jou finale antwoord is 5 - 3√2.

Prent getiteld Voeg vierkantswortels by en aftrek Stap 9

5. Doen voorbeeld 5. Kom ons probeer om die som van vierkantswortels te neem wat deel is van `n breuk. Net soos `n gewone breuk, kan jy nou net die som van breuke met dieselfde teller of noemer bereken. Kom ons sê jy werk met hierdie probleem: (√2)/4 + (√2)/2, Doen nou die volgende:

Maak seker dat hierdie terme dieselfde noemer het. Die minste gemene deler of noemer deelbaar deur beide `4` en `2` is `4`.

Dus, om die tweede term ((√2)/2) met `n noemer 4 te maak, moet jy beide die teller en die noemer met 2/2 vermenigvuldig. (√2)/2 x 2/2 = (2√2)/4.

Tel die noemer van die breuke bymekaar terwyl die noemer dieselfde bly. Doen net wat jy sou as jy breuke bytel. (√2)/4 + (2√2)/4 = 3√2)/4`.`

Wenke

Wortelgetalle met `n vierkant as `n faktor moet altyd vereenvoudig word vir jy gaan gelyke wortelgetalle bepaal en kombineer.

Waarskuwings

Jy kan nooit ongelyke wortelgetalle kombineer nie.
Jy kan nooit `n heelgetal en `n vierkantswortel kombineer nie. Dus: 3 + (2x) kan nie vereenvoudig word.