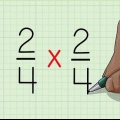Vereenvoudig wiskundige breuke

Inhoud

Trappe
Wenke
Waarskuwings

Wiskundige of algebraïese breuke lyk aanvanklik ongelooflik moeilik en kan vir die onopgeleide student skrikwekkend lyk om aan te pak. Met `n mengsel van veranderlikes, getalle en selfs eksponente is dit moeilik om te weet waar om te begin. Maar gelukkig is dieselfde reëls wat nodig is om gewone breuke te vereenvoudig, soos 15/25, ook van toepassing op wiskundige breuke.

Trappe

Metode 1 van 3: Vereenvoudiging van breuke

Prent getiteld Vereenvoudig algebraïese breuke Stap 1

1. Ken die woordeskat vir wiskundige breuke. Die volgende terme sal in die voorbeelde gebruik word, en is algemeen in probleme met breuke:

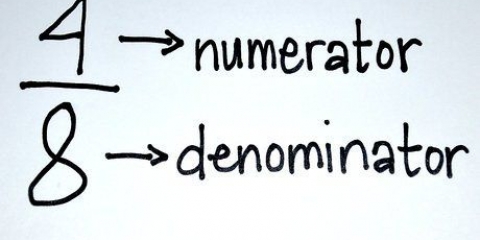
Teller: Die boonste deel van `n breuk (bv. (x+5)/(2x+3)).
Noemer: Die onderste deel van `n breuk (bv. (x+5)/(2x+3)).
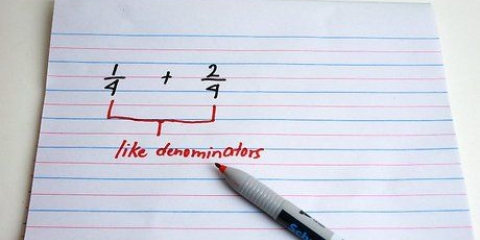
Gemene deler: Dit is `n getal waarmee jy beide die teller en noemer van `n breuk kan deel. Byvoorbeeld, in die breuk 3/9 is die gemene deler 3, aangesien beide getalle deur 3 gedeel kan word.
Faktor:` `n Getal wat vermenigvuldig word om `n ander getal te maak. Byvoorbeeld: die faktore van 15 is 1, 3, 5 en 15. Die faktore van 4 is 1, 2 en 4.
Vereenvoudigde vergelyking: Alle algemene faktore word verwyder en gelyke veranderlikes word gegroepeer (5x + x = 6x) totdat jy die eenvoudigste vorm van `n breuk, vergelyking of probleem verkry het. As jy niks meer met die breuk kan doen nie, word dit vereenvoudig.

Prent getiteld Vereenvoudig algebraïese breuke Stap 2

2. Vergelyk hoe om eenvoudige breuke op te los. Dit is presies dieselfde stappe wat jy sal neem om wiskundige breuke op te los. Neem die voorbeeld, 15/35. Om `n breuk te vereenvoudig, het ons nodig vind `n gemene deler. In hierdie geval kan albei getalle deur vyf gedeel word, sodat jy die 5 van die breuk kan deurtrek:
15→5 *3
35→5 *7
Nou kan jy slaan soos terme uit. In hierdie geval kan jy die twee vyfde deurtrek en jou vereenvoudigde antwoord laat, 3/7.

Prent getiteld Vereenvoudig algebraïese breuke Stap 3

3. Verwyder faktore uit algebraïese uitdrukkings net soos normale getalle. In die vorige voorbeeld kan jy maklik die 5 van 15 verwyder, en dieselfde beginsel geld vir meer komplekse uitdrukkings soos 15x - 5. Vind `n faktor wat beide getalle in gemeen het. Hier is die antwoord 5, want jy kan beide 15x en -5 deur die getal vyf deel. Soos voorheen, verwyder jy die gemeenskaplike faktor en vermenigvuldig dit met wat `oorbly`.`
15x - 5 = 5 *(3x - 1) Om jou werk na te gaan, vermenigvuldig net die vyf terug in die nuwe uitdrukking - jy sal eindig met dieselfde getalle waarmee jy begin het.

Prent getiteld Vereenvoudig algebraïese breuke Stap 4

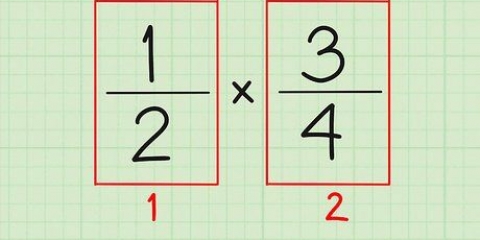
4. Nou kan jy komplekse terme uitvee net soos eenvoudige terme. Dieselfde beginsel as met gewone breuke werk ook vir wiskundige breuke. Dit is die maklikste manier om breuke te vereenvoudig. Neem die breuk:
(x+2)(x-3)
(x+2)(x+10)
Let op hoe die term (x+2) in beide die teller (bo) en die noemer (onder) voorkom. As sodanig kan jy hierdie verwyder om die algebraïese breuk te vereenvoudig, net soos jy die 5 van 15/35 verwyder het:
~~(x+2)~~(x-3)→(x-3)
~~(x+2)~~(x+10)→(x+10) Dit gee die finale antwoord: (x-3)/(x+10).

Metode 2 van 3: Vereenvoudiging van breuke

Prent getiteld Vereenvoudig algebraïese breuke Stap 5

1. Vind `n gemeenskaplike faktor in die teller (die boonste deel van die breuk). Die eerste ding om te doen wanneer `n algebraïese breuk vereenvoudig word, is om elke deel van die breuk te vereenvoudig. Begin met die boonste deel en trek soveel getalle as moontlik deur. As voorbeeld sal ons hierdie oefening gebruik:
9x-3
15x+6
Begin met die toonbank: 9x – 3. Daar is `n gemeenskaplike faktor vir beide 9x en -3, wat 3 is. Werk die 3 buite hakies soos jy enige ander getal sou doen, laat 3*(3x-1). Dit is jou nuwe toonbank:
3 (3x-1)
15x+6

Prent getiteld Vereenvoudig algebraïese breuke Stap 6

2. Vind `n gemeenskaplike faktor in die noemer.Deur die voorbeeld van bo af voort te sit, isoleer die noemer, 15x+6. Soek weer vir `n nommer wat by albei dele pas. Ook hier kan jy `n faktor van drie weglaat, sodat jy met 3 *(5x +2) oorbly. Inkorporeer jou nuwe noemer in die vergelyking:
3 (3x-1)
3 (5x+2)

Prent getiteld Vereenvoudig algebraïese breuke Stap 7

3. Verwyder soortgelyke terme. Dit is die stadium waar jy die breuk regtig kan vereenvoudig. Neem alle terme wat in beide die teller en die noemer is en verwyder hulle. In hierdie geval kan ons die 3 van beide bo en onder deurtrek.
3(3x-1)→(3x-1)
3(5x+2)→(5x+2)

Prent getiteld Vereenvoudig algebraïese breuke Stap 8

4. Weet wanneer die vergelyking heeltemal vereenvoudig is. `n Breuk word vereenvoudig wanneer daar nie meer algemene faktore in die bo- of onderkant is nie. Onthou, jy kan nie faktore van binne die hakies verwyder nie - in die voorbeeldprobleem kan jy nie die x van 3x en 5x faktoriseer nie, want die volle terme is eintlik (3x -1) en (5x + 2). Die voorbeeld is dus heeltemal vereenvoudig, met if die finale antwoord:
(3x-1)
(5x+2)

Prent getiteld Vereenvoudig algebraïese breuke Stap 9

5. Probeer `n oefenoefening. Die beste manier om te leer is om aan te hou probeer om wiskundige breuke te vereenvoudig. Die antwoorde is onder die probleme.
4(x+2)(x-13)
(4x+8)Antwoord: (x=13)
2x-x
5xAntwoord:(2x-1)/5

Metode 3 van 3: Truuks om moeiliker probleme op te los

Prent getiteld Vereenvoudig algebraïese breuke Stap 10

1. `Keer om` breuke om te faktoreer deur negatiewe getalle. Kom ons sê ons het die volgende vergelyking:
3(x-4)
5(4-x)
Let op hoe (x-4) en (4-x) amper is identies, maar jy kan hulle nie deurhaal nie, want hulle is omgekeerd. (x - 4) kan egter geskryf word as -1 *(4 - x) op dieselfde manier as wat jy (4 + 2x) herskryf as 2 *(2 + x). Dit word `buite die parentese bring` genoem.
-1 *3(4-x)
5(4-x)
Nou kan ons eenvoudig die twee identiese (4-x) weglaat:
-1 *3~~(4-x)~~
5~~(4-x)~~
Hieruit volg die finale antwoord: -3/5

Prent getiteld Vereenvoudig algebraïese breuke Stap 11

2. Herken die verskil van twee vierkante terwyl jy werk. Die verskil van twee vierkante is bloot om een kwadraatgetal van `n ander af te trek, soos die uitdrukking (a - b). Die verskil van perfekte vierkante word altyd in twee dele vereenvoudig, deur die vierkantswortels op te tel en af te trek. In elk geval kan jy die verskil van perfekte vierkante soos volg vereenvoudig:
a - b = (a+b)(a-b) Dit kan baie nuttig wees wanneer jy probeer om soortgelyke terme in wiskundige breuke te vind.

Voorbeeld: x - 25 = (x+5)(x-5)

Prent getiteld Vereenvoudig algebraïese breuke Stap 12

3. polinome te vereenvoudig. Polinome of polinome is komplekse algebraïese uitdrukkings met meer as twee terme, soos: x + 4x + 3. Gelukkig kan baie polinome vereenvoudig word deur `faktoring`. Die vorige uitdrukking kan byvoorbeeld herskryf word as (x+3)(x+1).

Prent getiteld Vereenvoudig algebraïese breuke Stap 13

4. Onthou dat veranderlikes ook in berekening gebring kan word. Dit is veral nuttig vir uitdrukkings met eksponente, soos x + x. Jy kan die grootste eksponent as `n faktor weglaat. In hierdie geval: x + x = x(x + 1).

Wenke

Gaan jou werk oor faktorisering na deur die faktor terug in die vergelyking te vermenigvuldig -- jy sal dieselfde getal kry waarmee jy begin het.
Skakel altyd die grootste getalle uit wat jy kan om jou vergelyking heeltemal te vereenvoudig.