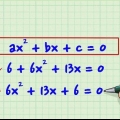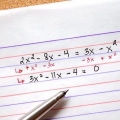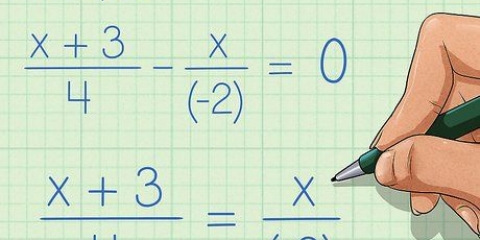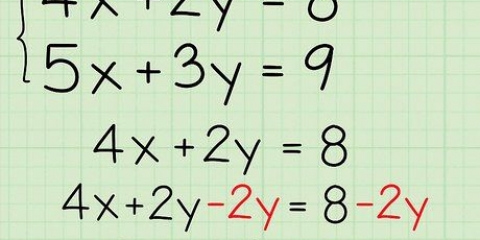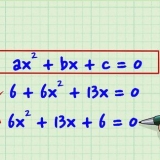Byvoorbeeld: as jy 20 in faktore wil verdeel, kan jy dit skryf as 4×5. Let daarop dat veranderlike terme ook as faktore geskryf kan word. - Byvoorbeeld, 20x kan geskryf word as 4(5x). Priemgetalle kan nie as faktore geskryf word nie, want hulle is slegs deur hulself en 1 deelbaar. 
huhvlermuise magt grootmaak Wruk Vvermeerder delen Otel aaftrek 

Byvoorbeeld, kom ons vind soortgelyke terme in ons vergelyking 1 + 2x - 3 + 4x. 2x en 4x het albei dieselfde veranderlike wat tot dieselfde mag verhef word (in hierdie geval het die x-veranderlikes glad geen eksponent nie). Verder is 1 en -3 gelyke terme, want nie een het `n veranderlike nie. So in hierdie vergelyking is 2x en 4x en 1 en-3 gelyke terme. 
Ons tel die soortgelyke terme in ons voorbeeld by. 2x + 4x = 6x 1 + -3 = -2 
In ons voorbeeld was die vereenvoudigde terme 6x en -2, so die nuwe uitdrukking word 6x-2. Hierdie vereenvoudigde uitdrukking is gelykstaande aan die oorspronklike (1 + 2x - 3 + 4x), maar is korter en makliker om te bereken met. Dit is makliker om te faktoriseer, wat, soos ons hieronder sal sien, `n belangrike vaardigheid is om te kan vereenvoudig. 
Gestel ons het byvoorbeeld die vergelyking 5(3x-1) + x((2x)/(2)) + 8 - 3x. Dan sal dit verkeerd wees om 3x en 2x dadelik as gelyke terme te beskou en dit te kombineer, want die hakies in die uitdrukking bepaal dat ons eers ander bewerkings moet doen. Kom ons voer eers die rekenkundige bewerkings in die uitdrukking uit volgens die volgorde van die bewerkings, om terme te kry wat ons het wel kan gebruik. Sien onder: 5(3x-1) + x((2x)/(2)) + 8 - 3x 15x - 5 + x(x) + 8 - 3x 15x - 5 + x + 8 - 3x. slaag nou aangesien die enigste bewerkings wat oorbly optel en aftrek is, kan ons dieselfde terme kombineer. x + (15x - 3x) + (8 - 5) x + 12x + 3 

Kom ons faktoriseer ons vergelyking deur die grootste gemene deler, 3, te gebruik. Ons doen dit deur elke term deur 3 te deel. 9x/3 = 3x 27x/3 = 9x -3/3 = -1 So die nuwe uitdrukking is 3x + 9x - 1. 
Vir ons voorbeeld uitdrukking, 3x + 9x - 1, plaas ons die uitdrukking tussen hakies en vermenigvuldig hierdie term met die grootste gemene deler van die oorspronklike vergelyking om om te skakel 3 (3x + 9x - 1) om te kry. Hierdie vergelyking is gelykstaande aan die oorspronklike, 9x + 27x - 3. 
Gestel ons oorspronklike voorbeelduitdrukking, 9x + 27x - 3, is gelyk aan die teller van `n groter breuk met 3 as die noemer. Hierdie breuk lyk soos volg: (9x + 27x - 3)/3. Ons kan faktorisering gebruik om hierdie breuk te vereenvoudig. Voeg die gefaktoriseerde vorm van ons oorspronklike uitdrukking by die teller: (3(3x + 9x - 1))/3 Let daarop dat beide die teller en noemer 3 as die koëffisiënt het. As jy die teller en noemer deur 3 deel, kry jy: (3x + 9x - 1)/1. Omdat `n breuk met "1" in die noemer gelyk is aan die terme in die teller, kan ons sê dat ons oorspronklike breuk vereenvoudig kan word tot 3x + 9x - 1. 

Kom ons neem `n eenvoudige voorbeeld - √(90). As ons die getal 90 as `n produk van die twee faktore, 9 en 10 neem, kan ons die vierkantswortel van 9 bereken om 3 te kry, en dit voor die radikaal plaas. Met ander woorde: (90) √(9×10) (√(9) × √(10)) 3 × √(10) 3√(10) 
Gestel ons het byvoorbeeld die uitdrukking 6x × 8x + (x/x). In enige geval waar dit nodig is om eksponente te vermenigvuldig of te deel, trek ons die eksponente onderskeidelik af of tel dit by om `n vereenvoudigde term vinnig op te los. Sien onder: 6x × 8x + (x/x) (6×8)x + (x) 48x + x Vir `n verduideliking, sien hieronder: Vermenigvuldiging van eksponensiële terme is in wese dieselfde as om lang reeks terme sonder eksponente te vermenigvuldig. Byvoorbeeld, omdat x = x × x × x en x= x × x × x × x × x, x × x = (x × x × x) × (x × x × x × x × x), of x. Net so is die deling van eksponensiële terme dieselfde as die verdeling van lang rye terme sonder eksponente. x/x = (x × x × x × x × x)/(x × x × x). Aangesien enige term in die teller uitgekanselleer kan word teen dieselfde term in die noemer, word ons gelaat met twee keer `n x in die teller en geen in die noemer, wat ons met x as die antwoord laat.
Vereenvoudiging van wiskundige vergelykings
Inhoud
Om algebraïese vergelykings te kan vereenvoudig, is `n noodsaaklike deel van die bemeestering van die basiese beginsels van algebra en `n uiters waardevolle hulpmiddel vir alle wiskundiges om te hê. Vereenvoudiging laat `n wiskundige toe om `n komplekse, lang en/of lomp uitdrukking in `n eenvoudiger of geriefliker maar ekwivalente vorm te verander. Die basiese beginsels van vereenvoudiging is redelik maklik om te leer - selfs vir iemand wat wiskunde haat. Deur `n paar eenvoudige stappe te volg is dit moontlik om baie van die mees algemene algebraïese uitdrukkings te vereenvoudig sonder enige spesiale wiskundige kennis.
Trappe
Metode 1 van 4: Verstaan sleutelbegrippe

1. Bepaal "gelyke terme" volgens hul veranderlikes en magte. Om in algebra te besit "gelyke terme" oor dieselfde veranderlikes, verhef tot dieselfde mag. Met ander woorde, twee terme is "soortgelyk", wanneer hulle dieselfde veranderlike(s) het, of glad nie, en wanneer elke veranderlike dieselfde krag het, of geen. Die volgorde van veranderlikes binne `n term maak nie saak nie.
- Byvoorbeeld, 3x en 4x is gelyke terme omdat elke term `n veranderlike x het wat tot die tweede mag verhef word. Die veranderlike x en x is nie gelyke terme nie, want x het `n ander mag in elke term. Net so is -3yx en 5xz nie gelyke terme nie, want elke term bestaan uit verskillende veranderlikes.

2. Faktoreer deur die getalle as die produk van twee faktore te skryf. Faktorisering is `n manier om `n gegewe getal as die produk van twee faktore te skryf. Getalle kan uit veelvuldige faktore saamgestel word – byvoorbeeld die getal 12, wat gevorm kan word deur 1 × 12, 2 × 6 en 3 × 4, sodat ons kan sê dat 1, 2, 3, 4, 6, en 12 is almal faktore van 12. Nog `n manier om daarna te kyk, is dat die faktore van `n getal die getalle is waarmee dit deelbaar is.

3. Gebruik die mnemonic `Hoe moet ons van die ontoereikendhede ontslae raak` (of as `n akroniem HMWVDOA) om die volgorde van die operasies te onthou. Soms is die vereenvoudiging van `n uitdrukking net om die bewerkings in die uitdrukking uit te voer totdat niks meer gedoen kan word nie. In daardie geval is dit belangrik om die volgorde van die bewerkings te ken, om berekeningsfoute te vermy. Hierdie mnemonic kan jou help om die volgorde van wysigings te onthou - die letters stem ooreen met die tipe wysigings wat jy moet uitvoer en in watter volgorde. As daar vermenigvuldiging en deling in dieselfde probleem is, sal jy daardie bewerkings van links na regs moet uitvoer wanneer jy by daardie punt kom. Dieselfde geld vir optel en aftrek. Die prent hierbo gee `n antwoord wat nie korrek is nie. Die laaste stap het nie optel en aftrekking van links na regs uitgewerk nie. Eers is dit bygevoeg. Daar moet 25 - 20 = 5 wees en dan 5 + 6 = 11.
Metode 2 van 4: Kombineer soortgelyke terme

1. Skryf jou vergelykings neer. Die eenvoudigste wiskundige vergelykings (dié met slegs `n paar veranderlikes en koëffisiënte as heelgetalle, sonder breuke, vierkantswortels, ens.) kan dikwels in `n paar stappe opgelos word. Soos met die meeste wiskundeprobleme, is die eerste stap om `n vergelyking te vereenvoudig om die vergelyking te skryf!
- Vir die volgende stappe neem ons die uitdrukking 1 + 2x - 3 + 4x as `n voorbeeld.

2. Bepaal wat soortgelyke terme is. Soek nou die soortgelyke terme in jou vergelyking. Onthou dat soortgelyke terme albei dieselfde veranderlike(s) en eksponent(e) het.

3. Kombineer soortgelyke terme. Noudat jy die soortgelyke terme bepaal het, kan jy hulle begin kombineer om jou vergelyking te vereenvoudig. Tel terme bymekaar (of trek dit af in die geval van negatiewe terme) om elke stel terme (met dieselfde veranderlikes en eksponente) in een term te vereenvoudig.

4. Maak `n vereenvoudigde uitdrukking van jou vereenvoudigde terme. Nadat jy jou soortgelyke terme gekombineer het, konstrueer `n uitdrukking uit jou nuwe, kleiner stel terme. Jy behoort nou `n eenvoudiger uitdrukking te hê met een term vir elke stel veranderlikes en eksponente in die oorspronklike uitdrukking. Hierdie nuwe uitdrukking is gelykstaande aan die eerste.

5. Hou by die volgorde van bewerkings wanneer soortgelyke terme kombineer. In baie eenvoudige uitdrukkings soos dié wat ons in die oefeninge hierbo behandel het, is dit maklik om die soortgelyke terme te herken. In die meer komplekse uitdrukkings, soos dié met terme tussen hakies, breuke en wortels, sal die kombinasie van soortgelyke terme nie onmiddellik duidelik wees nie. In daardie gevalle, volg die volgorde van bewerkings en voer die bewerkings uit op die terme in jou uitdrukking totdat jy net optel en aftrek.
Metode 3 van 4: Faktorering

1. Vind die grootste gemene deler in die uitdrukking. Faktorering is `n manier om uitdrukkings te vereenvoudig deur faktore wat in alle terme van die uitdrukking voorkom, te verwyder. Om te begin, vind die grootste gemene deler van alle terme in die uitdrukking - met ander woorde, die grootste getal waarmee alle terme in die uitdrukking deelbaar is deur.
- Gestel ons neem die vergelyking 9x + 27x - 3. Let daarop dat elke term in hierdie vergelyking deelbaar is deur 3. Omdat geen van die terme is volledig deelbaar deur `n ander, groter getal, ons kan dit sê 3 is die grootste gemene deler van ons uitdrukking.

2. Verdeel die terme in die uitdrukking deur die grootste gemene deler. Deel dan elke term in jou vergelyking deur die grootste gemene deler wat jy sopas gevind het. Die gevolglike terme sal almal kleiner koëffisiënte hê as dié in die oorspronklike uitdrukking.

3. Skryf jou uitdrukking as die produk van die grootste gemene deler en die oorblywende terme. Jou nuwe uitdrukking is nie dieselfde as die ou een nie, so dit is nie korrek om te sê dit is die vereenvoudigde weergawe nie. Om die nuwe uitdrukking gelyk te maak aan die ou een, sal ons in ag moet neem dat dit gedeel word deur die grootste gemene deler. Plaas jou nuwe uitdrukking tussen hakies en skryf die grootste gemene deler van die oorspronklike vergelyking as die koëffisiënt van die uitdrukking ook tussen hakies.

4. Faktor om breuke te vereenvoudig. Jy wonder dalk nou hoekom faktorisering nuttig is as die nuwe uitdrukking weer vermenigvuldig moet word nadat die grootste gemene deler verwyder is. Faktorering stel `n wiskundige in staat om `n aantal truuks te gebruik om `n uitdrukking te vereenvoudig. Een van die maklikste van hierdie truuks gebruik die feit dat die vermenigvuldiging van die teller en noemer van `n breuk met dieselfde getal `n breuk in dieselfde verhoudings produseer. Sien onder:
Metode 4 van 4: Pas vereenvoudig toe

1. Vereenvoudig breuke deur deur gelyke faktore te deel. Soos hierbo genoem, as die teller en noemer van `n uitdrukking dieselfde faktore het, kan hierdie faktore uit die breuk verwyder word. Soms vereis dit dat die teller, noemer of albei in berekening gebring moet word (soos die geval in die voorbeeld hierbo was), terwyl die gedeelde faktore in ander gevalle onmiddellik sigbaar is. Let daarop dat dit ook moontlik is om die individuele terme in die teller te deel deur die uitdrukking in die noemer, om `n vereenvoudigde uitdrukking te kry.
- Kom ons pak `n voorbeeld aan wat nie noodwendig vereis dat jy dit uitskryf om te vereenvoudig nie. Gestel jy het die breuk (5x + 10x + 20)/10, jy kan elke term in die teller deur die 10 in die noemer deel, om die geheel te vereenvoudig, selfs al is die "5" in 5x nie groter as 10 nie en dit is nie moontlik om 10 as `n faktor te kies nie.
- Deur dit te doen kry ons ((5x)/10) + x + 2. As ons wil, kan ons die eerste term herskryf as (1/2)x om (1/2)x + x + 2 te kry.

2. Gebruik vierkantswortels om wortels te vereenvoudig. Uitdrukkings onder die teken van `n vierkantswortel word vierkantswortelvergelykings genoem. Jy kan dit vereenvoudig deur die vierkantswortels (faktore wat self ’n tweede mag van ’n heelgetal vorm) te bepaal, waarna jy die vierkantswortel van hierdie faktore aftrek om hulle van die radikale teken te verwyder.

3. Tel die eksponente bymekaar wanneer jy twee eksponensiële terme vermenigvuldig, en trek hulle af wanneer jy deel. Sommige algebraïese vergelykings vereis vermenigvuldiging of deling van eksponensiële terme. Jy werk nie elke eksponensiële term uit nie en jy vermenigvuldig of deel nie met die hand nie, maar tel jy tel die eksponente van elke term op wanneer jy hulle saam vermenigvuldig en trek jy hulle wanneer jy dit deel, spaar jy baie tyd. Jy kan ook hierdie konsep toepas om vergelykings met veelvuldige veranderlikes te vereenvoudig.
Wenke
- Onthou dat jy hierdie getalle as positief of negatief moet beskou. Baie mense sit hiermee vas en dink, "Watter teken moet ek hier plaas?"
- Vra vir hulp as jy dit nodig het!
- Om wiskundige vergelykings te vereenvoudig is nie maklik nie, maar sodra jy dit onder die knie het, kan jy dit vir die res van jou lewe gebruik.
Waarskuwings
- Wees versigtig om nie per ongeluk ekstra getalle, eksponente of bewerkings by te voeg wat nie daar hoort nie.
- Gee altyd aandag aan gelyke terme en moenie dat die eksponente jou flous nie.
Artikels oor die onderwerp "Vereenvoudiging van wiskundige vergelykings"
Оцените, пожалуйста статью
Gewilde