Bereken die halfleeftyd van 'n stof: 8 stappe (met prente)

Inhoud

Trappe
- Deel 1 van 2: Berekening van die halfleeftyd
- Deel 2 van 2: Los halfleeftydkwessies op
Waarskuwings
Benodigdhede

Die halfleeftyd of halfleeftyd van `n stof wat met verloop van tyd verval is die tyd wat dit neem vir `n gegewe hoeveelheid van daardie stof om met die helfte te verval. In beginsel is hierdie term gereserveer vir die radioaktiewe verval van elemente soos uraan of plutonium, maar dit kan ook gebruik word vir enige stof wat onderhewig is aan verval, teen `n lineêre of eksponensiële tempo. Jy kan die halfleeftyd van enige stof bereken, mits die vervaltempo gegee word. Dit is die hoeveelheid van die stof waarmee jy begin en die hoeveelheid wat na `n sekere tyd oorbly. Lees verder om te leer hoe om die halfleeftyd van `n stof te bereken.

Trappe

Deel 1 van 2: Berekening van die halfleeftyd

Prent getiteld Bereken halfleeftyd Stap 1

1. Deel die hoeveelheid van `n stof op enige gegewe tydstip deur die hoeveelheid wat oorgebly het na `n sekere tydperk.

Die formule vir die berekening van die halfleeftyd is soos volg: t_1/2 = t * ln(2)/ln(N₀/N_t)
In hierdie formule sien ons die volgende veranderlikes: t = verstreke tyd, N₀ = hoeveelheid van `n stof vir die meting en N_t = hoeveelheid van `n stof na `n sekere tydperk.
Byvoorbeeld, as die hoeveelheid waarmee jy begin 1500 gram is en die finale hoeveelheid is 1000 gram, dan is 1500 / 1000 = 1,5. Ons sê dat die hoeveelheid tyd wat verloop het gelyk is aan (t) = 100 minute.

Prent getiteld Bereken halfleeftyd Stap 2

2. Bereken die logaritme (log) van die getal van die vorige stap. Al wat jy nou moet doen is om log(1,5) op jou sakrekenaar te tik.

Die log van `n getal met `n gegewe grondtal is die eksponent waarmee die grondtal verhoog word (of die aantal kere wat die grondtal met homself vermenigvuldig word) om daardie getal te kry. Log het basis 10. Die log-knoppie op jou sakrekenaar is `n gewone logaritme.

As jy daardie log (1.5) = 0.176 bereken, dam dit beteken dat die log van 1.5 gelyk is aan 0.176. Dit beteken weer dat 10 tot die 0,176 mag gelyk is aan 1,5.

Prent getiteld Bereken halfleeftyd Stap 3

3. Vermenigvuldig die verloop van tyd met log(2). Log(2) = 0,30103. Die verloop van tyd is 100 minute.

Byvoorbeeld, as die verloopte tyd gelyk is aan 100 minute, vermenigvuldig 100 met 0,30103. Hierdie resultaat is gelyk aan 30,103.

Prent getiteld Bereken halfleeftyd Stap 4

4. Deel die resultaat van die vorige berekening deur die getal van die tweede stap.

Dus, 30.103 / 0.176 = 171.04. Dit is die halfleeftyd van die stof uitgedruk in die tydseenheid van die derde stap.

Prent getiteld Bereken halfleeftyd Stap 5

5. Klaar. Noudat jy die halfleeftyd van hierdie voorbeeld gevind het, is dit goed om te weet dat jy die natuurlike logaritme (ln) kon gebruik het in plaas van die gewone log om dieselfde resultaat te kry. Trouens, die natuurlike logaritme word meer dikwels gebruik om die halfleeftyd te vind as die gewone log.

Dus,ln( 1.5) = 0.405 en ln(2) = 0.693. Dan volg: 0,693 x 100 = 69,3. Deel hierdie getal deur 0,405 en jy kry 171,04, dieselfde antwoord as met die normale log.

Deel 2 van 2: Los halfleeftydkwessies op

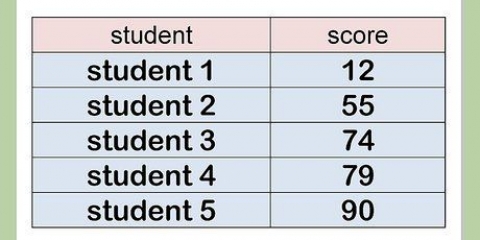
1. Bepaal hoeveel van `n stof met `n bekende halfleeftyd oor is na `n gegewe hoeveelheid dae. Los op: As 20 mg jodium-131 aan `n pasiënt gegee word, hoeveel is daar oor na 32 dae? Die halfleeftyd van jodium-131 is 8 dae. Hier is wat om te doen:

Bepaal hoeveel van die stof in 32 dae gehalveer word. Om dit te doen, deel 32 deur 8 (middel halfleeftyd). 32/8 = 4, dus word die stof 4 keer gehalveer.
Dit beteken dat jy na 8 dae steeds 20mg/2, of 10mg van die stof het; na 16 dae is dit steeds 10 mg/2 of 5 mg; na 24 dae het jy 5 mg/2, of 2,5 mg oor en na 32 dae is daar nog 2,5 mg/2, of 1,25 mg oor van die stof.

2. Bepaal die halfleeftyd van `n gegewe stof, met kennis van die begin- en eindhoeveelheid sowel as die verloop van tyd. Los die volgende probleem op: As `n laboratorium `n besending van 200g technetium-99m ontvang en net 12.5g van die isotoop oorbly, wat is die halfleeftyd van technetium-99m? Hier is wat om te doen:

Los hierdie van voor tot agter op. As 12,5 gram van die stof oorgebly het, was daar voor die halvering 25 g van die stof (12,5 x 2); voor dit was daar 50 g van die stof; weer daar vir 100 g, en jy het met 200 g begin.

Die stof moes dus 4 keer gehalveer word om van 200 g tot 12,5 g te kry, so jy kan bereken dat die halfleeftyd gelyk is aan 24 uur/4 = 6 uur.

3. Die vraag is hoeveel halverings nodig is om `n stof tot `n sekere hoeveelheid te verminder. Los die volgende op: As die halfleeftyd van uraan-232 70 jaar is, hoeveel halverings is nodig om 20 g van die stof tot 1,25 g te verminder? Hier is die effek:

Begin met 20 g en verminder dit. 20/2 = 10 (1 halvering), 10/2 = 5 (2 halverings), 5/2 = 2,5 (3 halverings) en 2,5/2 = 1,25 (4 halverings). Die antwoord is 4 helftes.

Waarskuwings

Halfleeftyd is `n skatting (per toeval) van die hoeveelheid tyd wat nodig is vir die helfte van die stof wat oorbly om te verval, eerder as `n presiese berekening. Byvoorbeeld, as daar net een atoom van `n sekere stof oor is, is halvering nie meer moontlik nie (of 1 of 0 atome bly oor). Hoe groter die hoeveelheid oorblyfsel, hoe meer akkuraat is die halfleeftydberekening, want jy het te doen met die wet van groot getalle.