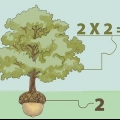
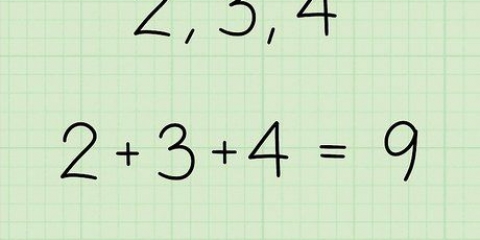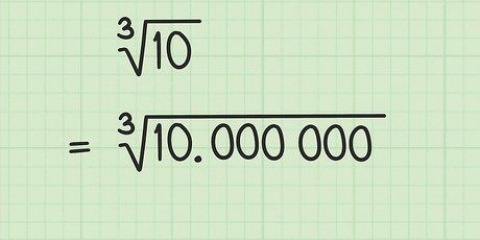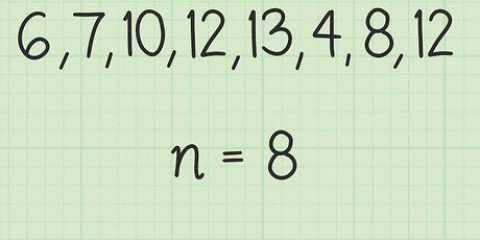Bv. 2 x 32 = 64. 
Bv. √64 = 8. 






Bv. 2,878521796 / 3 = 0,959507265 … 
Bv. inverse log 0,959507265 = 9,109766916. Dus is die meetkundige gemiddelde van 7, 9 en 12 gelyk aan 9.11. Die meetkundige gemiddelde van enige stel getalle is altyd kleiner as of gelyk aan die rekenkundige gemiddelde van daardie versameling. Die meetkundige gemiddelde is slegs van toepassing op positiewe getalle. In probleme waar die berekening van die meetkundige gemiddelde gevra word, maak dit gewoonlik min sin om met negatiewe getalle te werk.
Berekening van die meetkundige gemiddelde
Inhoud
Die meetkundige gemiddelde is `n wiskundige term wat verband hou met, en dikwels verwar word met, die meer algemeen gebruikte rekenkundige gemiddelde. Om die meetkundige gemiddelde te bereken, gebruik ons een van die metodes hieronder.
Trappe
Metode 1 van 4: Twee getalle: maklike metode

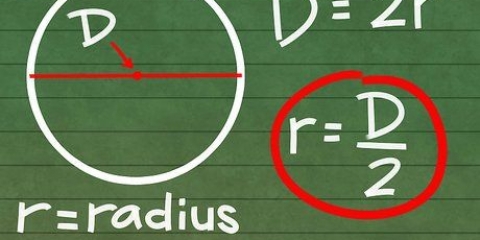
1. Bepaal watter getalle jy die gemiddeld van wil bereken.
- Bv. 2 en 32.

2. Vermenigvuldig hulle saam.

3. Bereken die vierkantswortel van die resulterende produk.
Metode 2 van 4: Twee nommers: gedetailleerde metode

1. Begin om die getalle in die vergelyking hieronder in te vul. Byvoorbeeld, as jy met die nommers 10 en 15 werk, voer 10 en 15 in soos hieronder getoon.

2. Los op vir x. Begin Kruisvermenigvuldiging. Aangesien x*x = x, sal jou vergelyking so lyk: x = (produk van die ander twee getalle). Om vir x op te los, vind die vierkantswortel van hierdie produk. Met `n bietjie geluk sal dit met `n heelgetal uitkom. As dit nie die geval is nie, gee die getal in desimale, of laat die vierkantswortel, afhangende van die vereistes. Die voorbeeld wat gegee word, is in die vorm van `n vierkantswortel.
Metode 3 van 4: Drie of meer getalle: Eenvoudige metode

1. Vervang jou getalle in die vergelyking hieronder. Gemiddeld = (a1 × a2 ×. . .× an)
- a1 is jou eerste nommer en a2 is die tweede getal, ensovoorts
- n is die aantal getalle

2. Vermenigvuldig die getalle a1, a2, ens. met mekaar.

3. Bereken die nde wortel van hierdie getal. Dit is die meetkundige gemiddelde.
Metode 4 van 4: Drie of meer getalle: Logaritmes

1. Vind die log van elke nommer en tel hierdie waardes bymekaar. Vind die LOG-knoppie op jou sakrekenaar. Tik nou: (eerste getal) LOG + (tweede getal) LOG + (derde getal) LOG [+ log van die volgende getalle, indien enige] =. Moenie vergeet om die = anders sal jy net die log van die laaste getal sien, nie die totaal nie.
- Bv. log 7 + log 9 + log 12 = 2,878521796..

2. Verdeel die som van die logaritmiese waardes deur die aantal getalle wat jy saamgevoeg het. Wanneer jy die logs van die drie getalle bymekaargetel het, deel deur drie.

3. Vind die omgekeerde van die log van die resultaat. Hoe dit op `n sakrekenaar werk, hang van die vervaardiger af, maar elke goeie een het `n omgekeerde funksie. Raadpleeg jou handleiding om uit te vind waar dit geleë is. Die omgekeerde log in hierdie geval is die meetkundige gemiddelde.
Wenke
- Die verskil tussen die rekenkundige en meetkundige gemiddelde:
- As jy rekenkundige gemiddelde as jy 3, 4 en 18 wil bereken, doen dan 3 + 4 + 18 en deel hierdie som deur 3 (want daar is drie getalle). Dus 25/3 = 8,333.... Die rekenkundige gemiddelde beantwoord die vraag, "As alle getalle gelyk is, wat sal daardie getalle moet wees om by dieselfde totaal op te tel??"
- Dit meetkundige gemiddelde beantwoord die vraag korrek, "As alle getalle dieselfde grootte is, wat sal daardie getalle moet wees om te vermenigvuldig om dieselfde totaal te kry??" Dus om die meetkundige gemiddelde van 3, 4 en 18 te vind, sal ons 3 x 4 x 18 = 216 doen. Dan neem ons die derdemagswortel hiervan (want daar is drie getalle). Die antwoord is 6. Met ander woorde, aangesien 6 x 6 x 6 = 3 x 4 x 18, 6 is die meetkundige gemiddelde van 3, 4 en 18.
Artikels oor die onderwerp "Berekening van die meetkundige gemiddelde"
Оцените, пожалуйста статью
Soortgelyk
Gewilde