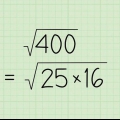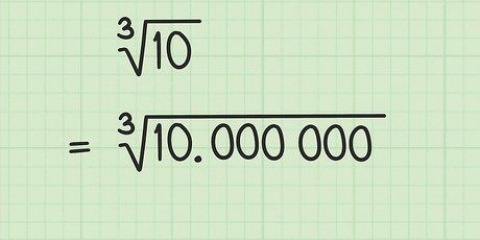Byvoorbeeld: 16 gedeel deur 4 is 4, en 4 gedeel deur 2 is 2, ens. Dus, in hierdie voorbeelde is 4 die vierkantswortel van 16, en 2 is die vierkantswortel van 4. Volmaakte vierkantswortels het geen breuke of desimale nie, want hulle is heelgetalle. 
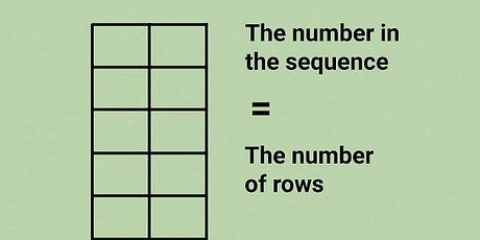
N is gelyk aan die getal waarvan jy die vierkantswortel wil bepaal. Dit sal binne die radikale teken geplaas word (onder die horisontale lyn). Dus, as jy die vierkantswortel van 9 wil vind, skryf jy die formule met die `N` (9) binne die radikaal, dan `n gelykheidsteken en die 3. Dit beteken dat die `vierkantswortel van 9 gelyk is aan 3.` 

Deel dan jou getal deur een van die vierkantswortelgetalle. Neem die antwoord en vind die gemiddeld van daardie getal en die getal waarmee jy gedeel het (die gemiddeld is die som van twee getalle gedeel deur twee). Neem dan die oorspronklike getal en deel dit deur die gemiddelde wat jy gekry het. Op die ou end vind jy die gemiddeld van daardie antwoord met die eerste gemiddelde wat jy gekry het. Klink dit ingewikkeld? `n Voorbeeld is waarskynlik die maklikste om te volg. Byvoorbeeld, 10 is tussen die twee perfekte vierkante 9 (3 x 3=9) en 16 (4 x 4=16). Die vierkantswortels van hierdie getalle is 3 en 4. Deel dus 10 deur die eerste getal, 3. Dit gee 3.33. Neem die gemiddeld van 3 en 3,33 (tel by en deel deur twee). Dit gee 3,1667. Deel nou 10 deur 3,1667. Die antwoord is 3,1579. Neem die gemiddelde van 3,1579 en 3,1667. Jy sal nou 3,1623 as `n antwoord kry. Kontroleer jou werk deur jou antwoord (in hierdie geval 3.1623) met homself te vermenigvuldig. En inderdaad: 3,1623 vermenigvuldig met 3,1623 is gelyk aan 10,001. 

Kyk ook of jou gewone sakrekenaar `n vierkantswortelsimbool het. `n Aanlyn sakrekenaar sal jou vra om die getal waarvan jy die vierkantswortel wil bereken in te voer en `n spesifieke knoppie te druk. Die rekenaar genereer dan die vierkantswortel van daardie getal.
Berekening van 'n vierkantswortel sonder 'n sakrekenaar
Inhoud
Om die vierkantswortel te bereken is maklik wanneer jy met `n heelgetal handel. Indien nie, is daar `n logiese prosedure wat jy kan volg om die vierkantswortel sistematies te bereken, met of sonder `n sakrekenaar. Hiervoor moet jy egter eers vermenigvuldig, optel en deel.
Trappe
Metode 1 van 3: Bepaling van die vierkantswortel van `n heelgetal

1. Vind die perfekte vierkantswortel met `n vermenigvuldiging. Die vierkantswortel van `n getal is enige getal wat, vermenigvuldig met homself, gelyk is aan die eerste getal. Nog `n manier om dit te sê is: `Wat kan ons met onsself doen? vermeerder om die nommer van die werkopdrag te kry?`
- Byvoorbeeld, die vierkantswortel van 1 is 1, want 1 vermenigvuldig met 1 is gelyk aan 1 (1 x 1=1). Die vierkantswortel van 4 is egter 2, want 2 vermenigvuldig met 2 is gelyk aan 4 (2 x 2=4). Dink aan die vierkantswortelkonsep deur `n eikeboom voor te stel. `n Eikeboom groei uit `n eikel. Dit is dus groter as, maar verwant aan die eikel, wat aan die wortel van die boom is. In die voorbeeld hierbo is 4 die wortel en 2 is die eikel.
- Dus is die vierkantswortel van 9 3 (3 x 3=9), van 16 is 4 (4 x 4=16), van 25 is 5 (5 x 5=25), van 36 is 6 (6 x 6=36) ), van 49 is 7 (7 x 7=49), van 64 is 8 (8 x 8=64), van 81 is 9 (9 x 9=81), en van 100 is 10 (10 x 10=100).

2. Gebruikdele om die vierkantswortel te vind. Om die vierkantswortel van `n heelgetal te vind, kan jy die heelgetal deel totdat jy `n antwoord kry wat dieselfde is as die getal waarmee jy die heelgetal deel.

3. Gebruik die korrekte simbole vir die vierkantswortel. Wiskundiges gebruik `n spesiale simbool, die radikale teken, om die vierkantswortel aan te dui. Dit lyk soos `n regmerkie met `n horisontale lyn aan die bokant wat na regs wys.
Metode 2 van 3: Vind die vierkantswortel van ander getalle

1. Maak `n skatting en gebruik `n eliminasieproses. Dit is moeiliker om die vierkantswortels van ander getalle as heelgetalle te bepaal. Maar dit is moontlik.
- Gestel jy wil die vierkantswortel van 20 bepaal. Jy weet dat 16 `n perfekte heelgetal is waarvan die vierkantswortel 4 is (4 x 4=16). Net so het 25 die vierkantswortel van 5 (5 x 5=25), dus moet die vierkantswortel van 20 iewers tussenin val.
- Jy kan skat dat die vierkantswortel van 20 gelyk is aan 4,5. Jy vier nou 4.5 om jou antwoord te kontroleer. Dit beteken om die getal met homself te vermenigvuldig: 4,5 x 4,5. Kyk of hierdie antwoord bo of onder 20 val. As jou raaiskoot nie lyk nie, probeer net `n ander raaiskoot (miskien 4.6 of 4.4) en verkort jou raaiskoot totdat jy by 20 kom.
- Byvoorbeeld, 4,5 x 4,5 = 20,25, dus moet jy `n kleiner getal probeer, iets soos 4,4. 4,4 x 4,4=19,36. Die vierkantswortel of van 20 is dus tussen 4,5 en 4,4. Wat van 4,445 x 4,445? Dit is 19 758. Ons kom nader. As jy dit aanhou doen, sal jy uiteindelik by 4,475 x 4,475 = 20,03 uitkom. Afgerond is dit 20.

2. Gebruik gemiddeldes. In beginsel probeer jy ook die naaste heelgetalle vind waartussen jou getal val.
Metode 3 van 3: Kwadratering van negatiewe getalle

1. Vierkantige negatiewe getalle met dieselfde proses. Onthou dat `n negatiewe getal vermenigvuldig met `n negatiewe getal `n positiewe getal produseer. Dus sal die kwadraat van `n negatiewe getal `n positiewe getal vorm.
- Byvoorbeeld, -5 x -5 =25. Onthou egter dat 5 x 5=25. Die vierkantswortel van 25 is dus -5 of 5. In beginsel het daardie getal twee vierkantswortels.
- Net so is 3 x 3=9 en -3 x -3=9, dus is die vierkantswortel van 9 beide 3 en -3. Die positiewe getal het die primêre wortel, so op hierdie punt is die enigste antwoord wat jy nodig het.

2. Gebruik ten slotte `n sakrekenaar. Dit is goed om te verstaan hoe om hierdie berekeninge met die hand te doen, maar daar is baie sakrekenaars aanlyn wat die vierkantswortel van `n getal kan bereken.
Wenke
- Dit word sterk aanbeveel om die eerste paar perfekte blokkies te memoriseer:
- 0=0, 1=1, 3=9, 4=16, 5=25, 6=36, 7=49, 8=64, 9=81, 10=100,
- Leer ook hierdie: 11=121, 12=144, 13 169, 14=196, 15=225, 16=256, 17=289...
- Meer voorbeelde om wiskunde makliker te maak: 10=100, 20=400, 30=900, 40=1600, 50=2500, ...
Artikels oor die onderwerp "Berekening van 'n vierkantswortel sonder 'n sakrekenaar"
Оцените, пожалуйста статью
Soortgelyk
Gewilde