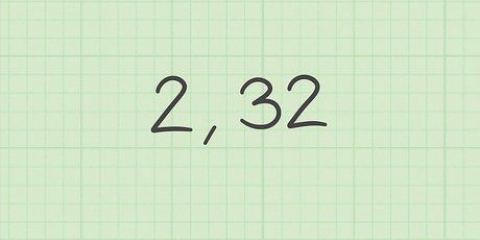Berekening van die Fibonacci-volgorde (met prente)

Inhoud

Trappe
- Metode 1 van 2: Gebruik `n tabel
- Metode 2 van 2: Gebruik Binet se formule en die Goue Gemiddelde

Die Fibonacci-reeks is `n reeks getalle wat gegenereer word deur die vorige twee getalle in die ry by te voeg. Die getalle in die reeks word gereeld in die natuur en in kuns gesien, soos spirale en die goue verhouding. Die maklikste manier om die reeks te bereken is om `n tabel voor te berei; dit is egter nie prakties as jy byvoorbeeld die 100ste term in die ry soek nie, in welke geval jy Binet se formule sal gebruik.

Trappe

Metode 1 van 2: Gebruik `n tabel

Prent getiteld Bereken die Fibonacci-volgorde Stap 1

1. Skep `n tabel met twee kolomme. Die aantal rye hang af van die aantal getalle in die Fibonacci-reeks wat jy wil bereken.

Byvoorbeeld, as jy die vyfde nommer in die ry wil vind, sal jou tabel vyf rye hê.
Met hierdie tabelmetode is dit nie moontlik om enige getal verder af in die ry te vind sonder om eers al die getalle voor dit te bereken nie. Byvoorbeeld, as jy die 100ste nommer in die ry wil vind, sal jy eers die eerste 99 nommers moet vind. Daarom werk die tabelmetode slegs vir getalle aan die begin van die ry.

Prent getiteld Bereken die Fibonacci-volgorde Stap 2

2. Tik die volgorde van getalle in die linkerkolom. Dit beteken om `n reeks opeenvolgende rangtelgetalle in te vul, wat begin met "1ste."

Die term verwys na die getal se posisie in die Fibonacci-reeks.

Byvoorbeeld, as jy die vyfde getal in die ry wil bereken, sal jy 1ste, 2de, 3de, 4de, 5de in die linkerkolom skryf. Dit sal jou help om die eerste vyf terme van die ry te identifiseer.

Prent getiteld Bereken die Fibonacci-volgorde Stap 3

3. Plaas 1 in die eerste ry van die regterkolom. Dit is die beginpunt van die Fibonacci-reeks. Met ander woorde, die eerste term in die ry is 1.

Die korrekte Fibonacci-volgorde begin altyd met 1. As jy met `n ander nommer wil begin, sal jy nie die korrekte patroon van die Fibonacci-reeks vind nie.

Prent getiteld Bereken die Fibonacci-volgorde Stap 4

4. Tel die eerste term (1) en 0. saam aan. Dit sal jou die tweede nommer in die ry gee.

Onthou dat om `n gegewe nommer van die Fibonacci-reeks te vind, moet jy net die twee vorige getalle bymekaar tel.

Om die ry te skep, kom 0 voor 1 (die eerste term), dus: 1 + 0 = 1.

Prent getiteld Bereken die Fibonacci-volgorde Stap 5

5. Voeg die eerste term (1) en die tweede term (1) saam. Dit sal jou die derde nommer in die ry gee.

1 + 1 = 2. Die derde kwartaal is 2.

Prent getiteld Bereken die Fibonacci-volgorde Stap 6

6. Tel die tweede term (1) en die derde term (2) saam om die vierde getal in die ry te kry.

1 + 2 = 3. Die vierde kwartaal is 3.

Prent getiteld Bereken die Fibonacci-volgorde Stap 7

7. Voeg die derde term (2) en die vierde term (3) saam. Nou ken jy die vyfde getal in die ry.

2 + 3 = 5. Die vyfde kwartaal is 5.

Prent getiteld Bereken die Fibonacci-volgorde Stap 8

8. Voeg die vorige twee getalle bymekaar om enige gegewe getal in die Fibonacci-reeks te vind. As jy hierdie metode gebruik, gebruik jy die formule

f n = f_{n - 1} + f_{n - 2}

$F_{{n}}=F_{{n-1}}+F_{{n-2}}$ . Omdat dit nie `n geslote formule is nie, kan jy dit nie gebruik om elke term in die reeks te bereken sonder om eers al die voorafgaande getalle te bereken nie.

Metode 2 van 2: Gebruik Binet se formule en die Goue Gemiddelde

Prent getiteld Bereken die Fibonacci-volgorde Stap 9

1. Skryf die formule neer:

X n

$x_{{n}}$ =

φ n - (1 - φ)^{n} \sqrt{5}

${frac{phi ^{{n}}-(1-phi )^{{n}}}{{sqrt{5}}}}$ . In die formule,

X n

$x_{{n}}$ = die term in die ry wat jy probeer vind,

n

$n$ = die posisienommer van die term in die reeks, en

φ

$fi$ = die goue verhouding.

Dit is `n geslote formule, so jy kan `n spesifieke term in die reeks bereken sonder om al die voriges te bereken.
Hierdie formule is `n vereenvoudigde formule wat afgelei is van Binet se Fibonacci-formule.
Die formule pas die goue verhouding toe ( $φ$ $fi$ ), want die verhouding van twee opeenvolgende getalle in die Fibonacci-ry is baie soortgelyk aan die goue verhouding.

Prent getiteld Bereken die Fibonacci-volgorde Stap 10

2. Pas die nommer vir n{displaystyle n} $n$ van toepassing op die formule. Die

n

$n$ verteenwoordig die term waarna jy soek in die ry.

As jy byvoorbeeld die vyfde nommer in die ry soek, voer 5 in. Jou formule behoort nou so te lyk:

X 5

$x_{{5}}$ =

φ 5 - (1 - φ)^{5} \sqrt{5}

${frac{phi ^{{5}}-(1-phi )^{{5}}}{{sqrt{5}}}}$ .

Prent getiteld Bereken die Fibonacci-volgorde Stap 11

3. Vervang die goue verhouding in die formule. Gebruik 1,618034 as `n benadering van die goue verhouding.

As jy byvoorbeeld vir die vyfde nommer in die ry soek, sal die formule wat jy ingevoer het soos volg lyk:

X 5

$x_{{5}}$ =

(1, 618034) 5 - (1 - 1, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(1-1,618034)^{{5}}}{{sqrt{5}}}}$ .

Prent getiteld Bereken die Fibonacci-volgorde Stap 12

4. Voltooi die berekeninge tussen hakies. Oorweeg die volgorde van rekenkundige bewerkings deur eers die deel tussen hakies te bereken:

1 - 1, 618034 = - 0, 618034

$1-1,618034=-0,618034$ .

In die voorbeeld word die vergelyking

X 5

$x_{{5}}$ =

(1, 618034) 5 - (- 0, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(-0.618034)^{{5}}}{{sqrt{5}}}}$ .

Prent getiteld Bereken die Fibonacci-volgorde Stap 13

5. Bereken die eksponente. Vermenigvuldig die twee getalle tussen hakies in die teller met die toepaslike eksponent.

In die voorbeeld,

1, 618034 5 = 11, 090170

$1,618034^{{5}}=11,090170$ ;

- 0, 618034 5 = - 0, 090169

$-0,618034^{{5}}=-0,090169$ . So word die vergelyking

X 5 = 11, 090170 - (- 0, 090169) \sqrt{5}

$x_{{5}}={frac{11,090170-(-0.090169)}{{sqrt{5}}}}$ .

Prent getiteld Bereken die Fibonacci-volgorde Stap 14

6. Voltooi die berekening. Voordat jy verder deel, moet jy eers die twee getalle in die teller aftrek.

In die voorbeeld,

11, 090170 - (- 0, 090169) = 11, 180339

$11,090170-(-0,090169)=11,180339$ , so word die vergelyking

X 5

$x_{{5}}$ =

11, 180339 \sqrt{5}

${frac{11,180339}{{sqrt{5}}}}$ .

Prent getiteld Bereken die Fibonacci-volgorde Stap 15

7. Verdeel deur die vierkantswortel van vyf. Die vierkantswortel van vyf word tot 2,236067 afgerond.

In die voorbeeldopdrag,

11, 180339 2, 236067 = 5, 000002

${frac{11,180339}{2,236067}}=5,000002$ .

Prent getiteld Bereken die Fibonacci-volgorde Stap 16

8. Rond af tot die naaste heelgetal. Jou antwoord is `n desimale getal, maar is baie naby aan `n heelgetal. Hierdie heelgetal verteenwoordig die getal in die Fibonacci-reeks.

As jy die volle goue verhouding gebruik het en niks afgerond het nie, sal jy `n heelgetal kry. Dit is egter meer prakties om af te rond, wat `n desimaal tot gevolg sal hê.

In die voorbeeld sal jou antwoord, bereken met `n sakrekenaar, ongeveer 5,000002 wees. Afgerond tot die naaste heelgetal, sal jou antwoord vyf wees, wat ook die vyfde getal in die Fibonacci-reeks sal wees.