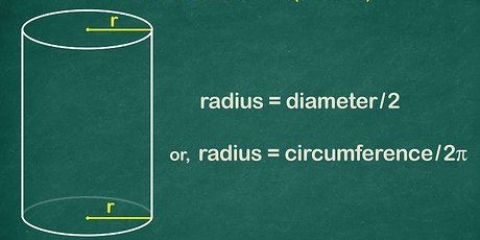
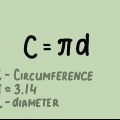Byvoorbeeld, as die deursnee van `n sirkel 4 is, dan is die reguit 4/2, of 2. 

Byvoorbeeld, as die omtrek 15 is, dan is die radius r = 15/2π, of 2.39. 


a = √(3 + 4) a = √(9 + 16) a = √25 a = 5 
b= √(-7 + -6) b = √(49 + 36) b = √85 b = 9.23 
c= √(4 + 2) c = √(16 + 4) c = √20 c = 4.47 
Die lengtes van die driehoek is soos volg: a = 5, b = 9.23 en c = 4.47. Die formule vir die radius lyk dus soos volg: r = (5 * 9.23*4.47)/(√(5 + 4.47 + 9.23)(4.47 + 9.23 - 5)(9.23 + 5 - 4.47)(5 + 4.47 – 9.23)). 
(a * b * c) = (5 * 9.23*4.47) = 206.29 r = (206.29)/(√(5 + 4.47 + 9.23)(4.47 + 9.23 - 5)(9.23 + 5 - 4.47)(5 + 4.47 – 9.23)) 
(a + b + c) = (5 + 4.47 + 9.23) = 18.7 (b + c - a) = (4.47 + 9.23 - 5) = 8.7 (c + a - b) = (9.23 + 5 - 4.47) = 9.76 (a + b - c) = (5 + 4.47 – 9.23) = 0.24 r = (206.29)/(√(18.7)(8.7)(9.76)(0.24)) 
(18.7)(8.7)(9.76)(0.24) = 381.01 r = 206.29/√381.01 
√381.01 = 19.51 r = 206.29/19.52 
r = 10.57
Berekening van die radius van 'n sirkel
Inhoud
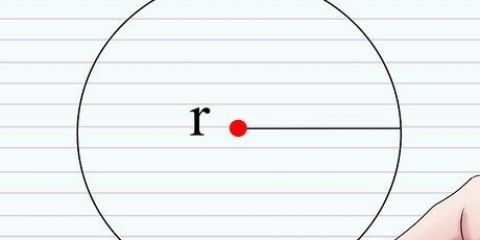
Die radius van `n sirkel is die afstand vanaf die middel van die sirkel na die rand. Die deursnee van `n sirkel is die lengte van die reguit lyn wat tussen twee punte op die sfeer of sirkel en deur sy middelpunt getrek kan word.Jy word dikwels gevra om die radius van `n sirkel te bereken op grond van ander data. In hierdie artikel sal jy leer hoe om die radius van `n sirkel te bereken op grond van `n gegewe deursnee, omtrek en area. Die vierde metode is `n meer gevorderde metode om die middelpunt en radius van `n sirkel te bepaal gebaseer op die koördinate van drie punte op die sirkel.
Trappe
Metode 1 van 3: Bereken die radius as jy die deursnee ken

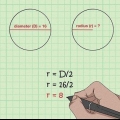
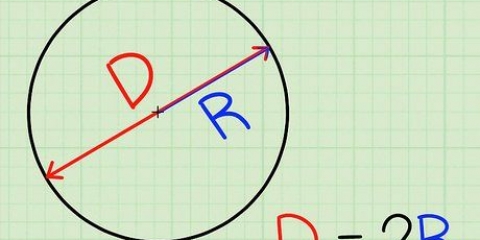
1. Onthou wat die deursnee is. Die deursnee van `n sirkel is die lengte van die reguit lyn wat tussen twee punte op die sfeer of sirkel en deur sy middelpunt getrek kan word. Die deursnee is die langste lyn wat deur `n sirkel getrek kan word en die sirkel in twee helftes verdeel. Die lengte van die deursnee is ook gelyk aan die lengte van twee keer die radius. Die formule vir die deursnee is soos volg: D= 2r, waar "d" staan vir deursnee en "r" vir balk. Die formule vir die radius kan van die vorige formule afgelei word en is dus: r = D/2.

2. Verdeel die deursnee deur 2 om die radius te vind. As jy die deursnee van `n sirkel ken, hoef jy dit net deur 2 te deel om die radius te vind.
Metode 2 van 3: Bereken die radius as jy die omtrek ken

1. Onthou jy die formule vir die omtrek van `n sirkel?. Die omtrek van `n sirkel is die afstand om die sirkel. Nog `n manier om daarna te kyk is die volgende: die omtrek is die lengte van die lyn wat jy kry as jy die sirkel op `n punt oopsny en die lyn reguit lê. Die formule vir die omtrek van `n sirkel is O = 2πr, waar "r" is die radius en π is die konstante pi, of 3,14159... Die formule vir die radius is dan r = O/2π.
- Gewoonlik kan jy pi tot twee syfers na die desimale punt (3,14) afrond, maar maak eers seker met jou onderwyser.

2. Bereken die radius met die omtrek wat gegee word. Om die radius op grond van die omtrek te bereken, deel die omtrek deur 2π, of 6.28
Metode 3 van 3: Bereken die radius as jy die koördinate van drie punte op die sirkel ken

1. Verstaan dat drie punte `n sirkel kan definieer. Enige drie punte op `n rooster definieer `n sirkel wat aan die drie punte raak. Dit is die omskrewe sirkel van die driehoek wat die punte vorm. Die middelpunt van die sirkel kan binne of buite die driehoek val, afhangende van die posisie van die drie punte, en terselfdertyd is dit die "kruising" van die driehoek.Dit is moontlik om die radius van die sirkel te bereken as jy die xy-koördinate van die drie betrokke punte ken.
- As `n voorbeeld, kom ons neem drie punte wat soos volg gedefinieer word: P1 = (3,4), P2 = (6, 8) en P3 = (-1, 2).

2. Gebruik die afstandsformule om die lengtes van die drie sye van die driehoek te bereken, wat ons a, b en c noem. Die formule vir die afstand tussen twee koördinate (x1, y1) en (x2, y2) is soos volg: afstand = √(( x2 - X1) + (j2 - y1)). Verwerk nou die koördinate van die drie punte in hierdie formule om die lengtes van die drie sye van die driehoek te vind.

3. Bereken die lengte van die eerste sy a, wat van punt P1 na P2 loop. In ons voorbeeld, die koördinate van P1 (3.4) en van P2 (6.8), dus die lengte van sy a = √((6 - 3) + (8 - 4)).

4. Herhaal die proses om die lengte van die tweede sy b te vind, wat van P2 na P3 loop. In ons voorbeeld is die koördinate van P2 (6.8) en van P3 (-1.2), dus die lengte van sy b = √((-1 - 6) + (2 - 8)).

5. Herhaal die proses om die lengte van die derde sy c te vind, wat van P3 na P1 loop. In ons voorbeeld, die koördinate van P3 (-1,2) en van P1 (3,4), dus die lengte van sy c =√((3 - -1) + (4 - 2)).

6. Gebruik hierdie lengtes in die radius-vindformule: (abc)/(√(a + b + c)(b + c - a)(c + a - b)(a + b - c)).. Die resultaat is die radius van ons sirkel!

7. Vermenigvuldig eers die drie lengtes saam om die teller van die breuk te vind. Dan pas jy die formule aan.

8. Bereken die somme tussen hakies. Plaas dan die resultate in die formule.

9. Vermenigvuldig die waardes in die noemer.

10. Neem die vierkantswortel van die produk om die noemer van die breuk te vind.

11. Deel nou die teller deur die noemer om die radius van die sirkel te vind!
Artikels oor die onderwerp "Berekening van die radius van 'n sirkel"
Оцените, пожалуйста статью
Soortgelyk
Gewilde