Byvoorbeeld, jy het `n seshoek met `n lengte van 8 cm vir die sy. Die basis van enige gelyksydige driehoek is dus 8 cm. 
Byvoorbeeld, as die basis van die gelyksydige driehoek 8 cm is, dan is die basis van enige reghoekige driehoek -- wanneer jy die driehoek in twee reghoekige driehoeke verdeel -- nou gelyk aan 4 cm. 
Byvoorbeeld, as die regte driehoek `n skuinssy van  een kant van
een kant van  en `n ander kant van omtrent
en `n ander kant van omtrent  (
( ), dan stel die Pythagoras-stelling dat
), dan stel die Pythagoras-stelling dat  , wat korrek is as jy dit uitwerk:
, wat korrek is as jy dit uitwerk:  .
. 
Byvoorbeeld, as die lengte van die basis 4 is, sal jou formule soos volg lyk:  .
. 
Byvoorbeeld, as die lengte van die sy van die seshoek 8 cm is, dan is die lengte van die skuinssy van die regte driehoek ook 8 cm. So jou formule sal nou soos volg lyk:  .
. 
Byvoorbeeld, nadat jy die bekende waardes gekwadraeer het, sal jou formule soos volg lyk:  .
. 
Byvoorbeeld:



Gebruik byvoorbeeld `n sakrekenaar wat jy bereken  . Die ontbrekende lengte van die regte driehoek, en dus die lengte van die apoteem van die seshoek, is dus gelyk aan 6,93 cm.
. Die ontbrekende lengte van die regte driehoek, en dus die lengte van die apoteem van die seshoek, is dus gelyk aan 6,93 cm. 

Byvoorbeeld, vir `n seshoek met `n sylengte van 8 cm, sal die formule soos volg lyk:  .
. 
Byvoorbeeld:  .
. 
Byvoorbeeld,  , waarmee die formule nou so lyk:
, waarmee die formule nou so lyk:  .
. 
Byvoorbeeld, die raaklyn van 30 is ongeveer 0,577, so die formule sal soos volg lyk:  .
. 
Byvoorbeeld:



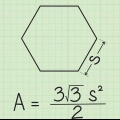
Die apotem van `n gereelde seshoek met sye van 8 cm is dus ongeveer 6,93 cm.
Berekening van die apoteem van 'n seshoek
Inhoud
`n Seshoek is `n veelhoek met ses hoeke en sye. Wanneer `n seshoek reëlmatig is, het dit ses gelyke sye en `n apoteem. `n Apoteem is `n lynstuk vanaf die middel van `n veelhoek na die middel van elke sy. Gewoonlik moet die lengte van die apotem gegee word om die oppervlakte van `n seshoek te bereken. Solank jy die lengte van die sy van die seshoek weet, kan jy die lengte van die apoteem bereken.
Trappe
Metode 1 van 2: Gebruik die Pythagoras-stelling (radiuslengte word gegee)

1. Verdeel die seshoek in ses kongruente gelyksydige driehoeke. Om dit te doen, trek `n lyn van elke hoekpunt of punt na die teenoorgestelde hoekpunt.

2. Kies `n driehoek en skryf die lengte van die basis neer. Dit is gelyk aan die lengte van die sy van die seshoek.

3. Maak twee reghoekige driehoeke. Jy doen dit deur `n lyn te trek vanaf die boonste hoekpunt van die gelyksydige driehoek loodreg op die basis. Hierdie lyn sal die basis van die driehoek halveer (dus is dit die apotem van die seshoek). Benoem die lengte van die basis van een van die reghoekige driehoeke.

4. Gebruik die Pythagoras-stelling. Die formule is  , waardeur
, waardeur  is gelyk aan die lengte van die skuinssy (die sy teenoor die regte hoek), en
is gelyk aan die lengte van die skuinssy (die sy teenoor die regte hoek), en  en
en  gelyk wees aan die lengtes van die ander twee sye van die driehoek.
gelyk wees aan die lengtes van die ander twee sye van die driehoek.
 , waardeur
, waardeur  is gelyk aan die lengte van die skuinssy (die sy teenoor die regte hoek), en
is gelyk aan die lengte van die skuinssy (die sy teenoor die regte hoek), en  en
en  gelyk wees aan die lengtes van die ander twee sye van die driehoek.
gelyk wees aan die lengtes van die ander twee sye van die driehoek. een kant van
een kant van  en `n ander kant van omtrent
en `n ander kant van omtrent  (
( ), dan stel die Pythagoras-stelling dat
), dan stel die Pythagoras-stelling dat  , wat korrek is as jy dit uitwerk:
, wat korrek is as jy dit uitwerk:  .
.
5. Vervang die lengte van die basis van die regte driehoek in die formule. Plaasvervanger vir  .
.
 .
. .
.
6. Vervang die lengte van die skuinssy in die formule. Jy ken die lengte van die skuinssy omdat jy die lengte van die seshoek ken. Die lengte van die sy van `n reëlmatige seshoek is gelyk aan die radius van die seshoek. Die radius is `n lyn wat die middelpunt van `n veelhoek met een van sy hoekpunte verbind. Jy sal sien dat die skuinssy van die regte driehoek ook die radius van die seshoek is, dus is die lengte van die sy van die seshoek gelyk aan die lengte van die skuinssy.
 .
.
7. Kwadra die bekende waardes van die formule. Onthou dat kwadratering van `n getal dieselfde is as om daardie getal met homself te vermenigvuldig.
 .
.
8. Isoleer die onbekende veranderlike. Jy doen dit deur die kwadraatwaarde af te trek  van beide kante van die vergelyking.
van beide kante van die vergelyking.
 van beide kante van die vergelyking.
van beide kante van die vergelyking.


9. Los op vir a  . Jy doen dit deur die vierkantswortel van elke sy van die vergelyking te bepaal. Dit sal jou die lengte van die ontbrekende sy van die driehoek gee, wat gelyk is aan die lengte van die apoteem van die seshoek.
. Jy doen dit deur die vierkantswortel van elke sy van die vergelyking te bepaal. Dit sal jou die lengte van die ontbrekende sy van die driehoek gee, wat gelyk is aan die lengte van die apoteem van die seshoek.
 . Jy doen dit deur die vierkantswortel van elke sy van die vergelyking te bepaal. Dit sal jou die lengte van die ontbrekende sy van die driehoek gee, wat gelyk is aan die lengte van die apoteem van die seshoek.
. Jy doen dit deur die vierkantswortel van elke sy van die vergelyking te bepaal. Dit sal jou die lengte van die ontbrekende sy van die driehoek gee, wat gelyk is aan die lengte van die apoteem van die seshoek. . Die ontbrekende lengte van die regte driehoek, en dus die lengte van die apoteem van die seshoek, is dus gelyk aan 6,93 cm.
. Die ontbrekende lengte van die regte driehoek, en dus die lengte van die apoteem van die seshoek, is dus gelyk aan 6,93 cm.Metode 2 van 2: Gebruik trigonometrie (en `n gegewe radius)

1. Skryf die formule om die apoteem van `n gereelde veelhoek te vind. Die formule is  , waardeur
, waardeur  is gelyk aan die lengte van die sy van die veelhoek en
is gelyk aan die lengte van die sy van die veelhoek en  is gelyk aan die aantal sye van die veelhoek.
is gelyk aan die aantal sye van die veelhoek.
 , waardeur
, waardeur  is gelyk aan die lengte van die sy van die veelhoek en
is gelyk aan die lengte van die sy van die veelhoek en  is gelyk aan die aantal sye van die veelhoek.
is gelyk aan die aantal sye van die veelhoek.
2. Vervang die lengte van die sy in die formule. Moenie vergeet om die veranderlike te vervang nie  .
.
 .
. .
.
3. Voer die aantal sye in die formule in. `n Seshoek het 6 kante. Moenie vergeet om die veranderlike te vervang nie  .
.
 .
. .
.
4. Rond die berekening tussen hakies af. Dit gee jou die aantal grade wat nodig is om die raaklyn te bereken.
 , waarmee die formule nou so lyk:
, waarmee die formule nou so lyk:  .
.
5. Bepaal die raaklyn. Gebruik `n sakrekenaar of trigonometriese tabel hiervoor.
 .
.
6. Vermenigvuldig die raaklyn met 2 en deel dan die lengte van een sy deur hierdie getal. Hiermee het jy die lengte van die apoteem van jou seshoek bereken.



Die apotem van `n gereelde seshoek met sye van 8 cm is dus ongeveer 6,93 cm.
Wenke
- Die term `apothema` kan verwys na die werklike lynsegment of na die lengte van daardie lynsegment.
- Onthou dat hierdie metode slegs met gereelde seshoeke werk. Onreëlmatige seshoeke het geen apotem nie.
Artikels oor die onderwerp "Berekening van die apoteem van 'n seshoek"
Оцените, пожалуйста статью
Soortgelyk
Gewilde