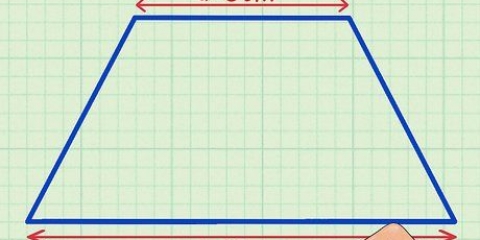
Byvoorbeeld, as jy `n trapezium het met `n bokant van 2 cm, `n onderkant van 3 cm en twee sylengtes van 1 cm, sal jou formule soos volg lyk:


Byvoorbeeld:


Die omtrek van die trapezium is dus 7 cm. 

Byvoorbeeld, as jy `n trapezium met `n hoogte van 6 cm het, moet jy `n lyn van elke boonste hoekpunt na die onderkant trek. Let op 6 cm vir elke lyn. 
Byvoorbeeld, as die bokant van die trapezium 6 cm is, dan is die middelste deel van die onderkant ook 6 cm. 

Byvoorbeeld, as jy weet dat die hoogte van die trapesium 6 cm is en die lengte van die sy (hypotenus) 9 cm is, sal jou vergelyking so lyk:


Byvoorbeeld: is die vergelyking  , dan vier jy 6 en 9, en trek die kwadraat van 6 af van die kwadraat van 9:
, dan vier jy 6 en 9, en trek die kwadraat van 6 af van die kwadraat van 9:




Byvoorbeeld:




Neem dus kennis as basis van die eerste driehoek.
as basis van die eerste driehoek. 
Byvoorbeeld, as die tweede kant van die trapesium 7 cm is, bereken soos volg:





Neem dus kennis as die basis van die tweede driehoek.
as die basis van die tweede driehoek. 
Byvoorbeeld: 
Nadat u die vierkantswortels na desimale omgeskakel het, het u
Dus, die benaderde omtrek van jou trapesium is 38,314 cm.. 

Byvoorbeeld, as jy `n trapezium met `n hoogte van 6 cm het, trek `n lyn van elke boonste hoekpunt na onder. Let op 6 cm by elke lyn. 
Byvoorbeeld, as die bokant van die trapezium 6 cm is, dan is die middelste deel van die onderkant ook 6 cm. 
Met hierdie verhouding kan jy die lengte van die skuinssy van die driehoek vind, wat ook die eerste sy van die trapesium is. Die skuinssy is die sy teenoor die 90 grade hoek van `n reghoekige driehoek. 
Gestel die gegewe binnehoek is 35 grade, en die hoogte van die driehoek is 6 cm, dan sal jou formule soos volg lyk:


As u byvoorbeeld `n sakrekenaar gebruik, sal u vind dat die sinus van `n 35 grade hoek 0,5738 is (afgerond). So jou formule is nou:


Byvoorbeeld:




Dus, die lengte van die skuinssy en die eerste ontbrekende kant van die trapesium is ongeveer 10,4566 cm. 
Byvoorbeeld, as die gegewe binnehoek 45 grade is, bereken:





Die lengte van die skuinssy en die tweede ontbrekende sy van die trapezium is dus ongeveer 8,4854 cm. 

Byvoorbeeld, as die eerste reghoekige driehoek `n skuinssy van 10,4566 en `n hoogte van 6 het, is jou formule:


Byvoorbeeld:






Dus is die basis van die driehoek en die eerste ontbrekende deel van die onderkant van die trapesium ongeveer 8,5639 cm. 
Byvoorbeeld, as die tweede regte driehoek `n skuinssy van 8,4854 en `n hoogte van 6 het, sal jy soos volg bereken:






So die basis van die tweede driehoek, en die tweede ontbrekende deel van die onderkant van die trapezium, is gelyk aan 6 cm. 
Byvoorbeeld: 
Die benaderde omtrek van die trapesium is dus 45,5059 cm.
Berekening van die omtrek van 'n trapesium
Inhoud
`n Trapesium word gedefinieer as `n vierhoek met twee parallelle sye. Soos met enige veelhoek, moet jy al vier sye bymekaar tel om die omtrek van `n trapesium (of trapesium) te vind. Dikwels sal jy egter sylengtes mis, maar jy het ander data, soos die hoogte van die trapezium, of die hoekmetings. Deur hierdie data te gebruik, kan jy die onbekende lengtes van die sye vind deur die reëls van meetkunde en trigonometrie te gebruik.
Trappe
Metode 1 van 3: As jy die lengte van beide kante en die basis ken

1. Stel die formule vir die omtrek van `n trapesium. Die formule is  , waardeur
, waardeur  is gelyk aan die omtrek van die trapesium, en die veranderlike
is gelyk aan die omtrek van die trapesium, en die veranderlike  gelyk aan die lengte van die bokant van die trapesium,
gelyk aan die lengte van die bokant van die trapesium,  gelyk aan die lengte van die onderkant,
gelyk aan die lengte van die onderkant,  is gelyk aan die lengte van die linkerkant en
is gelyk aan die lengte van die linkerkant en  gelyk aan die lengte van die regterkant.
gelyk aan die lengte van die regterkant.
 , waardeur
, waardeur  is gelyk aan die omtrek van die trapesium, en die veranderlike
is gelyk aan die omtrek van die trapesium, en die veranderlike  gelyk aan die lengte van die bokant van die trapesium,
gelyk aan die lengte van die bokant van die trapesium,  gelyk aan die lengte van die onderkant,
gelyk aan die lengte van die onderkant,  is gelyk aan die lengte van die linkerkant en
is gelyk aan die lengte van die linkerkant en  gelyk aan die lengte van die regterkant.
gelyk aan die lengte van die regterkant.
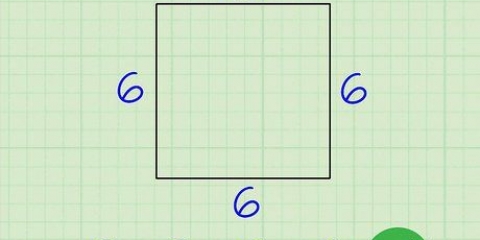
2. Gebruik die sylengtes in die formule. As jy nie die lengte van al vier sye van die trapezium ken nie, kan jy nie hierdie formule gebruik nie.


3. Voeg die sylengtes bymekaar. Dit sal jou die omtrek van jou trapezium gee.


Die omtrek van die trapezium is dus 7 cm.
Metode 2 van 3: As jy die hoogte ken, beide sylengtes en die boonste lengte

1. Verdeel die trapesium in `n reghoek en twee reghoekige driehoeke. Om dit te doen, teken die hoogte vanaf albei boonste hoeke.
- As jy nie die twee reghoekige driehoeke kan vorm nie omdat een sy van die trapesium loodreg op die basis is, maak seker dat hierdie sy dieselfde lengte as die hoogte is, en verdeel die trapesium in een reghoek en een regte driehoek.

2. Gee die lengte van elke kontoerlyn. Aangesien dit die teenoorgestelde sye van `n reghoek is, sal hulle dieselfde lengte wees.

3. Let op die lengte van die middelste deel van die onderkant. (Dit is die onderkant van die reghoek.) Die lengte sal gelyk wees aan die lengte van die bokant (die bokant van die reghoek), want die teenoorgestelde sye van `n reghoek is ewe lank. As jy nie die lengte van die bokant weet nie, kan jy nie hierdie metode gebruik nie.

4. Stel die Pythagoras-stelling vir die eerste reghoekige driehoek op. Die formule is  , waardeur
, waardeur  is die lengte van die skuinssy van die regte driehoek (die sy teenoor die regte hoek),
is die lengte van die skuinssy van die regte driehoek (die sy teenoor die regte hoek),  is die hoogte van die regte driehoek en
is die hoogte van die regte driehoek en  is die lengte van die basis van die driehoek.
is die lengte van die basis van die driehoek.
 , waardeur
, waardeur  is die lengte van die skuinssy van die regte driehoek (die sy teenoor die regte hoek),
is die lengte van die skuinssy van die regte driehoek (die sy teenoor die regte hoek),  is die hoogte van die regte driehoek en
is die hoogte van die regte driehoek en  is die lengte van die basis van die driehoek.
is die lengte van die basis van die driehoek.
5. Gebruik die bekende waardes van die eerste driehoek in die formule. Maak seker dat jy die sylengte van die trapezium intik vir  . Voer die hoogte van die trapezium in vir
. Voer die hoogte van die trapezium in vir  .
.
 . Voer die hoogte van die trapezium in vir
. Voer die hoogte van die trapezium in vir  .
.

6. Kwadreer die bekende waardes in die vergelyking. Trek dan die kwadraatwaardes van mekaar af om te kry  te isoleer.
te isoleer.
 te isoleer.
te isoleer. , dan vier jy 6 en 9, en trek die kwadraat van 6 af van die kwadraat van 9:
, dan vier jy 6 en 9, en trek die kwadraat van 6 af van die kwadraat van 9:



7. Neem die vierkantswortel om die waarde van te kry b  te vind. (Vir volledige instruksies oor die vereenvoudiging van vierkantswortels, lees hierdie artikel oor die onderwerp). Die resultaat sal jou die waarde gee van die ontbrekende basis van jou eerste reghoekige driehoek. Skryf hierdie lengte aan die basis van jou driehoek.
te vind. (Vir volledige instruksies oor die vereenvoudiging van vierkantswortels, lees hierdie artikel oor die onderwerp). Die resultaat sal jou die waarde gee van die ontbrekende basis van jou eerste reghoekige driehoek. Skryf hierdie lengte aan die basis van jou driehoek.
 te vind. (Vir volledige instruksies oor die vereenvoudiging van vierkantswortels, lees hierdie artikel oor die onderwerp). Die resultaat sal jou die waarde gee van die ontbrekende basis van jou eerste reghoekige driehoek. Skryf hierdie lengte aan die basis van jou driehoek.
te vind. (Vir volledige instruksies oor die vereenvoudiging van vierkantswortels, lees hierdie artikel oor die onderwerp). Die resultaat sal jou die waarde gee van die ontbrekende basis van jou eerste reghoekige driehoek. Skryf hierdie lengte aan die basis van jou driehoek.



Neem dus kennis
 as basis van die eerste driehoek.
as basis van die eerste driehoek.
8. Vind die ontbrekende lengte van die tweede regte driehoek. Om dit te doen, stel die Pythagoras-stelling vir die tweede driehoek op en volg die stappe om die lengte van die ontbrekende sy te vind. As jy met `n gelykbenige trapesium werk (die een waar die twee nie-parallelle sye dieselfde lengte het), dan is die twee reghoekige driehoeke kongruent, dus is die waarde van die eerste driehoek gelyk aan dié van die tweede driehoek.





Neem dus kennis
 as die basis van die tweede driehoek.
as die basis van die tweede driehoek.
9. Tel al die sylengtes van die trapezium by. Die omtrek van enige veelhoek is die som van alle sye:  . Vir die onderkant, voeg die onderkant van die reghoek by, plus die basisse van die twee driehoeke. Jy sal waarskynlik vierkantswortels in jou antwoord hê. Vir volledige instruksies oor die byvoeging van vierkantswortels, lees die artikel oor hierdie onderwerp. Jy kan ook `n sakrekenaar gebruik om die vierkantswortels na desimale om te skakel.
. Vir die onderkant, voeg die onderkant van die reghoek by, plus die basisse van die twee driehoeke. Jy sal waarskynlik vierkantswortels in jou antwoord hê. Vir volledige instruksies oor die byvoeging van vierkantswortels, lees die artikel oor hierdie onderwerp. Jy kan ook `n sakrekenaar gebruik om die vierkantswortels na desimale om te skakel.
 . Vir die onderkant, voeg die onderkant van die reghoek by, plus die basisse van die twee driehoeke. Jy sal waarskynlik vierkantswortels in jou antwoord hê. Vir volledige instruksies oor die byvoeging van vierkantswortels, lees die artikel oor hierdie onderwerp. Jy kan ook `n sakrekenaar gebruik om die vierkantswortels na desimale om te skakel.
. Vir die onderkant, voeg die onderkant van die reghoek by, plus die basisse van die twee driehoeke. Jy sal waarskynlik vierkantswortels in jou antwoord hê. Vir volledige instruksies oor die byvoeging van vierkantswortels, lees die artikel oor hierdie onderwerp. Jy kan ook `n sakrekenaar gebruik om die vierkantswortels na desimale om te skakel.
Nadat u die vierkantswortels na desimale omgeskakel het, het u

Dus, die benaderde omtrek van jou trapesium is 38,314 cm..
Metode 3 van 3: As jy die hoogte, lengte van die boonste en onderste binnehoeke ken

1. Verdeel die trapesium in `n reghoek en twee reghoekige driehoeke. Dui hiervoor die hoogte vanaf albei boonste hoeke aan.
- As jy nie twee reghoekige driehoeke kan vorm nie omdat een sy van die trapesium loodreg op die basis is, maak seker dat hierdie sy dieselfde grootte as die hoogte is, en verdeel die trapesium in een reghoek en een regte driehoek.

2. Benoem elke kontoer. Aangesien dit teenoorgestelde sye van `n reghoek is, sal hulle dieselfde lengte hê.

3. Let op die lengte van die middelste deel van die onderkant. (Dit is die onderkant van die reghoek.) Hierdie lengte sal gelyk wees aan die lengte van die bokant, want die teenoorgestelde sye van `n reghoek is ewe lank.

4. Stel die sinusformule vir die eerste reghoekige driehoek op. Die formule is  , waardeur
, waardeur  die binnehoek is,
die binnehoek is,  die hoogte van die driehoek en
die hoogte van die driehoek en  is die lengte van die skuinssy.
is die lengte van die skuinssy.
 , waardeur
, waardeur  die binnehoek is,
die binnehoek is,  die hoogte van die driehoek en
die hoogte van die driehoek en  is die lengte van die skuinssy.
is die lengte van die skuinssy.
5. Gebruik die bekende waardes in die sinusverhouding. Maak seker dat jy die hoogte van die driehoek gebruik as die lengte van die teenoorgestelde sy in die formule. jy los dit op vir H.


6. Bepaal die sinus van die hoek. Doen dit deur die SIN-knoppie op `n wetenskaplike sakrekenaar te gebruik. Gebruik hierdie waarde in die formule.


7. Los dit op vir H. Om dit te doen, vermenigvuldig elke sy met H en deel dan elke sy deur die sinushoek. Of deel die hoogte van die driehoek deur die sinushoek.




Dus, die lengte van die skuinssy en die eerste ontbrekende kant van die trapesium is ongeveer 10,4566 cm.

8. Bepaal die lengte van die skuinssy van die tweede regte driehoek. Stel die sinusformule ( ) vir die tweede gegewe binnehoek. Dit sal jou die lengte van die skuinssy gee, wat ook die eerste kant van die trapezium is.
) vir die tweede gegewe binnehoek. Dit sal jou die lengte van die skuinssy gee, wat ook die eerste kant van die trapezium is.
 ) vir die tweede gegewe binnehoek. Dit sal jou die lengte van die skuinssy gee, wat ook die eerste kant van die trapezium is.
) vir die tweede gegewe binnehoek. Dit sal jou die lengte van die skuinssy gee, wat ook die eerste kant van die trapezium is.




Die lengte van die skuinssy en die tweede ontbrekende sy van die trapezium is dus ongeveer 8,4854 cm.

9. Stel die Pythagoras-stelling vir die eerste reghoekige driehoek op. Die Pythagoras-stelling is hard  , waar die lengte van die skuinssy gelyk is aan
, waar die lengte van die skuinssy gelyk is aan  , en die hoogte van die driehoek
, en die hoogte van die driehoek  .
.
 , waar die lengte van die skuinssy gelyk is aan
, waar die lengte van die skuinssy gelyk is aan  , en die hoogte van die driehoek
, en die hoogte van die driehoek  .
.
10. Gebruik die bekende waardes in die Pythagoras-stelling vir die eerste reghoekige driehoek. Maak seker dat jy die korrekte waarde vir die skuinssy invoer  en die hoogte
en die hoogte  .
.
 en die hoogte
en die hoogte  .
.

11. Los dit op vir b  . Dit sal jou die lengte van die basis van die eerste reghoekige driehoek gee, en die eerste ontbrekende deel van die basis van die trapezium.
. Dit sal jou die lengte van die basis van die eerste reghoekige driehoek gee, en die eerste ontbrekende deel van die basis van die trapezium.
 . Dit sal jou die lengte van die basis van die eerste reghoekige driehoek gee, en die eerste ontbrekende deel van die basis van die trapezium.
. Dit sal jou die lengte van die basis van die eerste reghoekige driehoek gee, en die eerste ontbrekende deel van die basis van die trapezium.





Dus is die basis van die driehoek en die eerste ontbrekende deel van die onderkant van die trapesium ongeveer 8,5639 cm.

12. Vind die lengte van die ontbrekende basis van die tweede regte driehoek. Gebruik die Pythagoras-stelling ( ). Gebruik die lengte van die skuinssy vir
). Gebruik die lengte van die skuinssy vir  en die hoogte vir
en die hoogte vir  . Los dit op vir
. Los dit op vir  en jy kry die lengte van die tweede ontbrekende deel van die bodem die trapezium.
en jy kry die lengte van die tweede ontbrekende deel van die bodem die trapezium.
 ). Gebruik die lengte van die skuinssy vir
). Gebruik die lengte van die skuinssy vir  en die hoogte vir
en die hoogte vir  . Los dit op vir
. Los dit op vir  en jy kry die lengte van die tweede ontbrekende deel van die bodem die trapezium.
en jy kry die lengte van die tweede ontbrekende deel van die bodem die trapezium.





So die basis van die tweede driehoek, en die tweede ontbrekende deel van die onderkant van die trapezium, is gelyk aan 6 cm.

13. Voeg al die kante van die trapezium saam. Die omtrek van enige veelhoek is die som van alle sye:  . Vir die onderkant, voeg die onderkant van die reghoek by die basis van die twee driehoeke.
. Vir die onderkant, voeg die onderkant van die reghoek by die basis van die twee driehoeke.
 . Vir die onderkant, voeg die onderkant van die reghoek by die basis van die twee driehoeke.
. Vir die onderkant, voeg die onderkant van die reghoek by die basis van die twee driehoeke.
Die benaderde omtrek van die trapesium is dus 45,5059 cm.
Wenke
- Gebruik die wette van spesiale driehoeke om die ontbrekende lengtes van spesiale driehoeke te vind, sonder om die sinusformule of die Pythagoras-stelling te gebruik. Die wette is van toepassing op `n 30-60-90 driehoek, of `n 90-45-45 driehoek.
- Gebruik `n wetenskaplike sakrekenaar om die sinus van `n hoek te bepaal deur die hoek in te voer en dan die `SIN`-knoppie te druk. Jy kan ook `n trigonometrietabel gebruik.
Benodigdhede
- Sakrekenaar
- Potlood
- Papier
Artikels oor die onderwerp "Berekening van die omtrek van 'n trapesium"
Оцените, пожалуйста статью
Soortgelyk
Gewilde