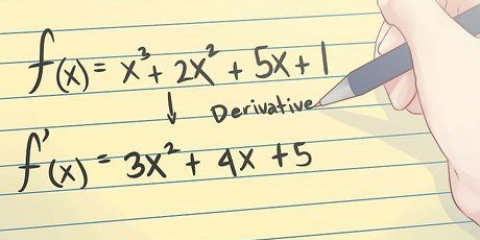Vind die afgeleide van die vierkantswortel van x

Inhoud

Trappe

As jy wiskunde op skool geneem het, moes jy die magsreël geleer het om die afgeleide van eenvoudige funksies te bepaal. Wanneer die funksie egter `n vierkantswortel of radikaal bevat, soos $\sqrt{X}$ ${sqrt{x}}$ , dan blyk die magsreël moeilik toe te pas. Deur `n eenvoudige vervanging van eksponente te gebruik, word die bepaling van die afgeleide van so `n funksie baie maklik. Jy kan dan dieselfde substitusie toepas en die kettingreël gebruik om die afgeleide van baie ander funksies met wortels te vind.

Trappe

Metode 1 van 3: Die toepassing van die magsreël

Prent getiteld Onderskei die vierkantswortel van X Stap 1

1. Kyk weer na die magsreël vir afgeleide instrumente. Die eerste reël wat jy waarskynlik geleer het om afgeleides te vind, is die reël van mag. Hierdie reël sê dat vir `n veranderlike

X

$X$ tot die mag van `n getal

a

$a$ , is die afgeleide, en word soos volg bereken:

$f (X) = X a$ ${displaystyle f(x)=x^{a}}$
$f seks (X) = a X^{a - 1}$ ${displaystyle f^{prime}(x)=ax^{a-1}}$
Kyk na die volgende voorbeeldfunksies en hul afgeleides:

as $f (X) = X 2$ ${displaystyle f(x)=x^{2}}$ , dan $f seks (X) = 2 X$ ${displaystyle f^{prime }(x)=2x}$
as $f (X) = 3 X 2$ ${displaystyle f(x)=3x^{2}}$ , dan $f seks (X) = 2 * 3 X = 6 X$ ${displaystyle f^{prime }(x)=2*3x=6x}$
as $f (X) = X 3$ ${displaystyle f(x)=x^{3}}$ , dan $f seks (X) = 3 X^{2}$ ${displaystyle f^{prime }(x)=3x^{2}}$
as $f (X) = \frac{1}{2} X^{4}$ ${displaystyle f(x)={frac {1}{2}}x^{4}}$ , dan $f seks (X) = 4 * \frac{1}{2} X^{3} = 2 X^{3}$ ${displaystyle f^{prime}(x)=4*{frac {1}{2}}x^{3}=2x^{3}}$

Prent getiteld Onderskei die vierkantswortel van X Stap 2

2. Herskryf die vierkantswortel as eksponent. Om die afgeleide van `n vierkantswortelfunksie te vind, onthou dat die vierkantswortel van `n getal of veranderlike ook as `n eksponent geskryf kan word. Die term onder die radikale word as `n basis geskryf, en word verhef tot die mag 1/2. Die term word ook gebruik as `n eksponent van die vierkantswortel. Kyk deur die volgende voorbeelde:

\sqrt{X} = X^{\frac{1}{2}}

${displaystyle {sqrt {x}}=x^{frac {1}{2}}}$

\sqrt{4} = 4^{\frac{1}{2}}

${displaystyle {sqrt {4}}=4^{frac {1}{2}}}$

\sqrt{3 X} = (3 X)^{\frac{1}{2}}

${displaystyle {sqrt {3x}}=(3x)^{frac {1}{2}}}$

Prent getiteld Onderskei die vierkantswortel van X Stap 3

3. Pas die heerskappy van mag toe. As die funksie die eenvoudigste vierkantswortel is,

f (X) = \sqrt{X}

${displaystyle f(x)={sqrt {x}}}$ , pas dan die magsreël soos volg toe om die afgeleide te vind:

f (X) = \sqrt{X}

${displaystyle f(x)={sqrt {x}} }$ (Skryf die oorspronklike funksie neer.)

f (X) = X (\frac{1}{2})

${displaystyle f(x)=x^{({frac {1}{2}})} }$ (Skryf die wortel oor as `n eksponent.)

f seks (X) = \frac{1}{2} X^{(\frac{1}{2} - 1)}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{({frac {1}{2}}-1)} }$ (Vind die afgeleide deur die magsreël te gebruik.)

f seks (X) = \frac{1}{2} X^{(- \frac{1}{2})}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{(-{frac {1}{2}})} }$ (Vereenvoudig die eksponent.)

Prent getiteld Onderskei die vierkantswortel van X Stap 4

4. Vereenvoudig die resultaat. Op hierdie stadium moet jy weet dat `n negatiewe eksponent beteken dat jy die inverse neem van wat die getal met die positiewe eksponent sou wees. Die eksponent van

- \frac{1}{2}

${displaystyle -{frac {1}{2}}}$ beteken dat die vierkantswortel van die basis die noemer van `n breuk word.

Deur voort te gaan met die vierkantswortel van die funksie x van bo, kan die afgeleide soos volg vereenvoudig word:

f seks (X) = \frac{1}{2} X^{- \frac{1}{2}}

${displaystyle f^{prime }(x)={frac {1}{2}}x^{-{frac {1}{2}}}}$

f seks (X) = \frac{1}{2} * \frac{1}{\sqrt{X}}

${displaystyle f^{prime }(x)={frac {1}{2}}*{frac {1}{sqrt {x}}}}$

f seks (X) = 12 \sqrt{X}

${displaystyle f^{prime }(x)={frac {1}{2{sqrt {x}}}}}$

Metode 2 van 3: Die toepassing van die kettingreël vir vierkantswortelfunksies

Prent getiteld Onderskei die vierkantswortel van X Stap 5

1. Hersien die kettingreël vir funksies. Die kettingreël is `n reël vir afgeleides wat jy gebruik wanneer die oorspronklike funksie `n funksie binne `n ander funksie kombineer. Die kettingreël sê dit, vir twee funksies

f (X)

$f(x)$ en

g (X)

${displaystyle g(x)}$ , die afgeleide van die kombinasie van die twee funksies kan soos volg gevind word:

as $y = f (g (X))$ ${displaystyle y=f(g(x))}$ , dan $y seks = f^{seks} (g) * g^{seks} (X)$ ${displaystyle y^{prime }=f^{prime }(g)*g^{prime }(x)}$ .

Prent getiteld Onderskei die vierkantswortel van X Stap 6

2. Definieer die kettingreëlfunksies. Deur die kettingreël te gebruik, moet jy eers die twee funksies definieer waaruit jou gekombineerde funksie bestaan. Vir vierkantswortelfunksies is die buitenste funksie

f (g)

${displaystyle f(g)}$ die vierkantswortelfunksie en die binneste funksie

g (X)

${displaystyle g(x)}$ die funksie onder die radikale.

Byvoorbeeld: veronderstel jy het die afgeleide van

\sqrt{3 X + 2}

${displaystyle {sqrt {3x+2}}}$ wil vind. Definieer dan die twee dele soos volg:

f (g) = \sqrt{g} = g^{\frac{1}{2}}

${displaystyle f(g)={sqrt {g}}=g^{frac {1}{2}}}$

g (X) = (3 X + 2)

${displaystyle g(x)=(3x+2)}$

Prent getiteld Onderskei die vierkantswortel van X Stap 7

3. Vind die afgeleides van die twee funksies. Om die kettingreël op die vierkantswortel van `n funksie toe te pas, moet jy eers die afgeleide van die algemene vierkantswortelfunksie vind:

f (g) = \sqrt{g} = g^{\frac{1}{2}}

${displaystyle f(g)={sqrt {g}}=g^{frac {1}{2}}}$

f seks (g) = \frac{1}{2} g^{- \frac{1}{2}}

${displaystyle f^{prime }(g)={frac {1}{2}}g^{-{frac {1}{2}}}}$

f seks (g) = 12 \sqrt{g}

${displaystyle f^{prime }(g)={frac {1}{2{sqrt {g}}}}}$

Bepaal dan die afgeleide van die tweede funksie:

g (X) = (3 X + 2)

${displaystyle g(x)=(3x+2)}$

g seks (X) = 3

${displaystyle g^{prime }(x)=3}$

Prent getiteld Onderskei die vierkantswortel van X Stap 8

4. Kombineer die funksies in die kettingreël. Die kettingreël is

y seks = f^{seks} (g) * g^{seks} (X)

${displaystyle y^{prime }=f^{prime }(g)*g^{prime }(x)}$ . Kombineer die afgeleides soos volg:

y seks = 12 \sqrt{g} * 3

${displaystyle y^{prime }={frac {1}{2{sqrt {g}}}}*3}$

y seks = 12 \sqrt{(3 X + 2} * 3

${displaystyle y^{prime }={frac {1}{2{sqrt {(3x+2}}}}*3}$

y seks = 32 \sqrt{(3 X + 2}

${displaystyle y^{prime }={frac {3}{2{sqrt {(3x+2}}}}}$

Metode 3 van 3: Vind die afgeleides van wortelfunksies vinnig

Prent getiteld Onderskei die vierkantswortel van X Stap 9

1. Bepaal afgeleides van `n vierkantswortelfunksie deur `n vinnige metode te gebruik. Wanneer jy die afgeleide van die vierkantswortel van `n veranderlike of `n funksie wil vind, kan jy `n eenvoudige reël toepas: die afgeleide sal altyd die afgeleide van die getal onder die radikaal wees, gedeel deur dubbel die oorspronklike vierkantswortel. Simbolies kan dit voorgestel word as:

as $f (X) = \sqrt{jy}$ ${displaystyle f(x)={sqrt {u}}}$ , dan $f seks (X) = jy seks 2 \sqrt{jy}$ ${displaystyle f^{prime }(x)={frac {u^{prime}}{2{sqrt {u}}}}}$

Prent getiteld Onderskei die vierkantswortel van X Stap 10

2. Vind die afgeleide van die getal onder die radikaal. Dit is `n getal of funksie onder die vierkantswortelteken. Om hierdie vinnige metode te gebruik, vind net die afgeleide van die getal onder die radikaal. Kyk na die volgende voorbeelde:

In die funksie

\sqrt{5 X + 2}

${displaystyle {sqrt {5x+2}}}$ , is die wortelgetal

(5 X + 2)

${displaystyle (5x+2)}$ . Die afgeleide is

5

$5$ .

In die funksie

\sqrt{3 X} 4

${displaystyle {sqrt {3x^{4}}}}$ , is die wortelgetal

3 X 4

${displaystyle 3x^{4}}$ . Die afgeleide is

12 X 3

${displaystyle 12x^{3}}$ .

In die funksie

\sqrt{s i n (X)}

${displaystyle {sqrt {sin(x)}}}$ , is die wortelgetal

sonde (X)

${displaystyle sin(x)}$ . Die afgeleide is

\cos (X)

${displaystyle cos(x)}$ .

Prent getiteld Onderskei die vierkantswortel van X Stap 11

3. Skryf die afgeleide van die wortelgetal as die teller van `n breuk. Die afgeleide van `n vierkantswortelfunksie sal `n breuk bevat. Die teller van hierdie breuk is die afgeleide van die wortelgetal. Dus, in die voorbeeldfunksies hierbo, sal die eerste deel van die afgeleide soos volg verloop:

f (X) = \sqrt{5 X + 2}

${displaystyle f(x)={sqrt {5x+2}}}$ , dan

f seks (X) = \frac{5}{noemer}

${displaystyle f^{prime }(x)={frac {5}{text{noemer}}}}$

f (X) = \sqrt{3 X} 4

${displaystyle f(x)={sqrt {3x^{4}}}}$ , dan

f seks (X) = 12 X 3 noemer

${displaystyle f^{prime }(x)={frac {12x^{3}}{text{noemer}}}}$

f (X) = \sqrt{sonde (X)}

${displaystyle f(x)={sqrt {sin(x)}}}$ , dan

f seks (X) = \cos (X) noemer

${displaystyle f^{prime }(x)={frac {cos(x)}{text{noemer}}}}$

Prent getiteld Onderskei die vierkantswortel van X Stap 12

4. Skryf die noemer as dubbel die oorspronklike vierkantswortel. Met hierdie vinnige metode is die noemer twee keer die oorspronklike vierkantswortelfunksie. Dus in die drie voorbeeldfunksies hierbo is die noemers van die afgeleides:

f (X) = \sqrt{5 X + 2}

${displaystyle f(x)={sqrt {5x+2}}}$ , dan

f seks (X) = toonbank 2 \sqrt{5 X + 2}

${displaystyle f^{prime }(x)={frac {text{counter}}{2{sqrt {5x+2}}}}}$

f (X) = \sqrt{3 X} 4

${displaystyle f(x)={sqrt {3x^{4}}}}$ , dan

f seks (X) = toonbank 2 \sqrt{3 X} 4

${displaystyle f^{prime}(x)={frac {text{counter}}{2{sqrt {3x^{4}}}}}}}$

f (X) = \sqrt{sonde (X)}

${displaystyle f(x)={sqrt {sin(x)}}}$ , dan

f seks (X) = toonbank 2 \sqrt{sonde (X)}

${displaystyle f^{prime }(x)={frac {text{counter}}{2{sqrt {sin(x)}}}}}$

Prent getiteld Onderskei die vierkantswortel van X Stap 13

5. Kombineer die teller en noemer om die afgeleide te vind. Sit die twee helftes van die breuk saam en die resultaat sal die afgeleide van die oorspronklike funksie wees.