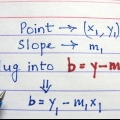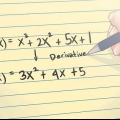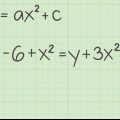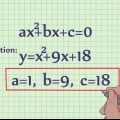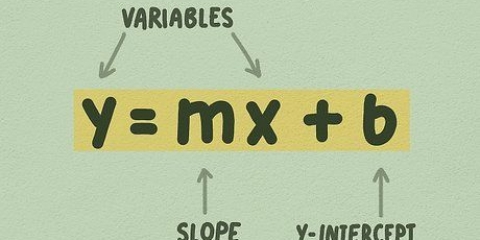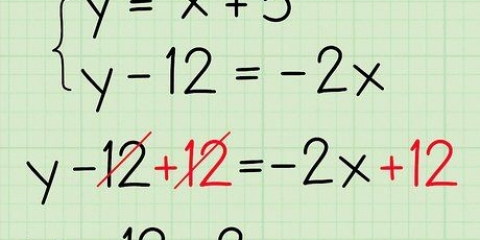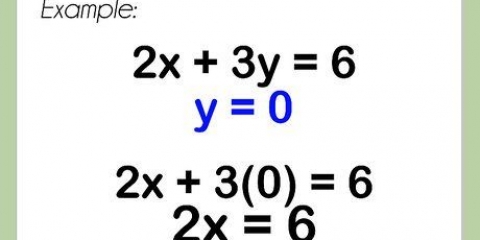Vind die snypunt van 'n vergelyking met die Y-as

Inhoud

Trappe
Wenke

Die y-afsnit van `n vergelyking is die punt waar die grafiek van `n vergelyking met die y-as sny. Daar is verskeie maniere om hierdie kruising te vind, afhangende van die inligting wat aan die begin van jou opdrag gegee word.

Trappe

Metode 1 van 3: Vind die kruising met die y-as deur die helling te gebruik

1. Let op die helling. Die helling van `y oor x` is `n enkele getal wat die helling van `n lyn aandui. Hierdie tipe probleem gee jou ook die (x,y)-koördinaat van `n punt op die grafiek. As jy nie albei hierdie besonderhede het nie, gaan voort met die ander metodes hieronder.

Voorbeeld 1: `n Reguit lyn met helling 2 gaan deur die punt (-3.4). Bepaal die snypunt met die y-as van hierdie lyn deur die stappe hieronder te gebruik.

2. Leer die gewone vorm van `n lineêre vergelyking. Enige reguit lyn kan geskryf word as y = mx + b. Wanneer die vergelyking in hierdie vorm is, is m die helling en die konstante b die kruising met die y-as.

3. Vervang die helling in hierdie vergelyking. Skryf die lineêre vergelyking neer, maar in plaas van m gebruik jy die helling van jou lyn.

Voorbeeld 1 (vervolg):y = mx + b
m = helling = 2
y = 2x + b

4. Vervang x en y met die koördinate van die punt. As jy die koördinate van `n punt op die lyn het, kan jy X en y-plaasvervanger koördinate vir die X en y in jou lineêre vergelyking. Doen dit vir die vergelyking van jou werkopdrag.

Voorbeeld 1 (vervolg): Die punt (3,4) is op hierdie lyn. op hierdie punt, x = 3 en y = 4.
Vervang hierdie waardes in y = 2X +b:
4 = 2(3) + b

5. Los op vir b. Moenie vergeet nie, b is die snypunt met die y-as van die lyn. Nou b is die enigste veranderlike in die vergelyking, herrangskik die vergelyking om vir hierdie veranderlike op te los en vind die antwoord.

Voorbeeld 1 (vervolg):4 = 2(3) + b
4 = 6 + b
4 - 6 = b
-2 = b
Die snypunt van hierdie lyn met die y-as is -2.

6. Skryf dit neer as `n koördinaat. Die snypunt met die y-as is die punt waar die lyn met die y-as sny. Aangesien die y-as deur die punt x = 0 gaan, is die x-koördinaat van die snyding met die y-as altyd 0.

Voorbeeld 1 (vervolg): Die snypunt met die y-as is by y = -2, dus is die koördinaatpunt (0, -2).

Metode 2 van 3: Gebruik twee punte

1. Let op die koördinate van beide punte. Hierdie metode handel oor probleme waarin slegs twee punte op `n reguit lyn gegee word. Skryf elke koördinaat in die vorm (x,y).

2. Voorbeeld 2: `n Reguit lyn gaan deur die punte (1, 2) en (3, -4). Bepaal die snypunt met die y-as van hierdie lyn deur die stappe hieronder te gebruik.

3. Bereken die x- en y-waardes. Die helling of helling is `n maatstaf van hoeveel die lyn in die vertikale rigting vir elke stap in die horisontale rigting beweeg. Jy ken dit dalk as `y oor x` (

\frac{y}{X}

${frac{y}{x}}$ ). Hier is hoe om hierdie waardes met behulp van twee punte te bepaal:

Die verandering van `y` is die verandering in vertikale rigting, of die verskil tussen die y-waardes van die twee punte.

Die verandering van `x` is die verandering in horisontale rigting, of die verskil tussen die X-waardes van die twee punte.

Voorbeeld 2 (vervolg): Die y-waardes van die twee punte is 2 en -4, so die lyn neem toe in die vertikale rigting met (-4) - (2) = -6.
Die x-waardes van die twee punte (in dieselfde volgorde) is 1 en 3, so die lyn vermeerder horisontaal met 3 - 1 = 2.

Prent getiteld Vind die Y-afsnit Stap 10

4. Deel y deur x om helling te bepaal. Noudat jy hierdie twee waardes ken, kan jy dit gebruik in `

\frac{y}{X}

${frac{y}{x}}$ ` vir die bepaling van die helling van die lyn.

Voorbeeld 2 (vervolg):

s l O bl e = \frac{y}{X} = - 6 2 =

$helling={frac{y}{x}}={frac{-6}{2}}=$ -3.

Prent getiteld Vind die Y-afsnit Stap 11

5. Kyk weer na die standaardvorm van `n lineêre vergelyking. Jy kan `n reguit lyn met die formule beskryf y = mx + b, waardeur m die helling is en b die kruising met die y-as. Noudat ons die helling het m en `n punt (x,y), kan ons hierdie vergelyking gebruik om te vind b om op te los (die kruising met die y-as).

Prent getiteld Vind die Y-afsnit Stap 12

6. Vul die helling en die punt in die vergelyking in. Neem die vergelyking in standaardvorm en vervang m volgens die helling wat jy bereken het. Vervang die veranderlikes X en y deur die koördinate van `n enkele punt op die lyn. Dit maak nie saak watter punt jy gebruik nie.

Voorbeeld 2 (vervolg): y = mx + b
Helling = m = -3, dus y = -3x + b
Die lyn gaan deur `n punt met (x,y)-koördinate (1,2), dus 2 = -3(1) + b.

Prent getiteld Vind die Y-afsnit Stap 13

7. Los op vir b. Nou is die enigste veranderlike wat in die vergelyking oorbly b, die kruising met die y-as. Herrangskik vergelyking sodat b aan die een kant van die vergelyking, en jy het jou antwoord. Onthou dat die snypunt met die y-as altyd `n x-koördinaat van 0 het.

Voorbeeld 2 (vervolg): 2 = -3(1) + b
2 = -3 + b
5 = b
Die kruising met die y-as is (0.5).

Metode 3 van 3: Gebruik `n vergelyking

Prent getiteld Vind die Y-afsnit Stap 14

1. Skryf die vergelyking van die lyn neer. As jy die vergelyking van die lyn het, kan jy die snypunt met die y-as met `n klein algebra bepaal.

Voorbeeld 3: Wat is die snypunt met die y-as van die lyn x + 4y = 16?
Let wel: Voorbeeld 3 is `n reguit lyn. Sien die einde van hierdie afdeling vir `n voorbeeld van `n kwadratiese vergelyking (gebruik `n veranderlike verhoog tot die mag van 2).

Prent getiteld Vind die Y-afsnit Stap 15

2. Vervang 0 vir x. Die y-as is `n vertikale lyn deur x = 0. Dit beteken dat enige punt op die y-as `n x-koördinaat van 0 het, insluitend die snypunt van die lyn met die y-as. Tik 0 vir x in die vergelyking.

Voorbeeld 3 (vervolg): x + 4y = 16
x = 0
0 + 4j = 16
4j = 16

Prent getiteld Vind die Y-afsnit Stap 16

3. Los op vir y. Die antwoord is die snypunt van die lyn met die y-as.

Voorbeeld 3 (vervolg): 4j = 16

4 y 4 = \frac{16}{4}

${frac{4y}{4}}={frac{16}{4}}$
y = 4.
Die snypunt van die lyn met die y-as is 4.

Prent getiteld Vind die Y-afsnit Stap 17

4. Bevestig dit deur `n grafiek te teken (opsioneel). Kontroleer jou antwoord deur die vergelyking so akkuraat as moontlik te teken. Die punt waar die lyn deur die y-as gaan, is die snypunt met die y-as.

Prent getiteld Vind die Y-afsnit Stap 18

5. Vind die snypunt met die y-as van `n kwadratiese vergelyking. `n Kwadratiese vergelyking het `n veranderlike (x of y) wat tot die tweede mag verhef word. Deur dieselfde substitusie te gebruik, kan jy y oplos, maar aangesien die kwadratiese vergelyking `n kromme is, kan dit die y-as sny by 0, 1 of 2 punte. Dit beteken dat jy met 0, 1 of 2 antwoorde sal eindig.

Voorbeeld 4: Om die kruising van te vind

y 2 = X + 1

$y^{2}=x+1$ met die y-as vervang jy x = 0 en los die kwadratiese vergelyking op.
In hierdie geval kan ons

y 2 = 0 + 1

$y^{2}=0+1$ los op deur die vierkantswortel van beide kante te neem. Onthou dat jy twee antwoorde kry wanneer jy `n vierkantswortel neem: `n negatiewe en `n positiewe antwoord.

\sqrt{y} 2 = \sqrt{1}

${sqrt{y^{2}}}={sqrt{1}}$
y = 1 of y = -1. Dit is albei snypunte met die y-as van hierdie kromme.

Wenke

Sommige lande gebruik a c of enige ander veranderlike vir b in die vergelyking y = mx + b. Die betekenis daarvan bly egter dieselfde; dit is net `n ander notasie.
Vir meer ingewikkelde vergelykings, kan jy die terme gebruik met y isoleer aan die een kant van die vergelyking.
Wanneer jy die helling tussen twee punte bereken, kan jy X en y-trek koördinate in enige volgorde af, solank jy die punt in dieselfde volgorde vir beide y en x plaas. Byvoorbeeld, die helling tussen (1, 12) en (3, 7) kan op twee verskillende maniere bereken word:

Tweede punt – eerste punt: $7 - 12 3 - 1 = - 5 2 = - 2.5$ ${frac{7-12}{3-1}}={frac{-5}{2}}=-2.5$
Eerste punt – tweede punt: $12 - 7 1 - 3 = 5 - 2 = - 2.5$ ${frac{12-7}{1-3}}={frac{5}{-2}}=-2.5$