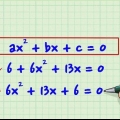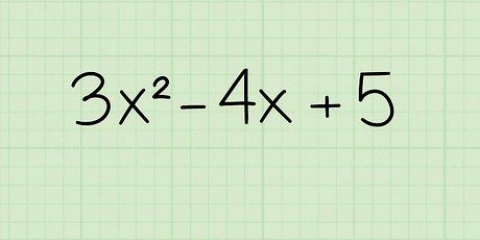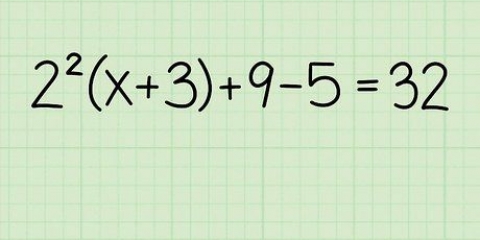Los kwadratiese vergelykings op

Inhoud

Trappe
Wenke

`n Kwadratiese vergelyking is `n vergelyking waar die grootste eksponent van `n veranderlike twee is. Drie van die mees gebruikte metodes om hierdie vergelykings op te los is: faktorisering, gebruik van die abc-formule, of deling van die vierkant. As jy wil weet hoe om hierdie metodes te bemeester, volg net hierdie stappe.

Trappe

Metode 1 van 3: Faktorering

Prent getiteld Los kwadratiese vergelykings op Stap 1 op

1. Skuif alle terme na een kant van die vergelyking. Die eerste stap in faktorisering is om alle terme na een kant van die vergelyking te skuif, wat x positief laat. Pas die optel- of aftrekbewerking toe op die terme x, die veranderlike x en die konstantes, beweeg hulle op hierdie manier na die een kant van die vergelyking en laat niks aan die ander kant. Hier is hoe dit werk:

2x - 8x - 4 = 3x - x =
2x +x - 8x -3x - 4 = 0
3x - 11x = 0

Prent getiteld Los Kwadratiese Vergelykings Stap 2 op

2. Faktoreer die uitdrukking. Om die uitdrukking te faktoriseer moet jy die faktore van 3x en die faktore van die konstante -4 faktoriseer om hulle te vermenigvuldig en dan bymekaar te tel om die waarde van die middelterm te gee, -11. Hier is hoe om dit te doen:

Aangesien 3x `n eindige aantal moontlike faktore het, 3x en x, kan jy dit tussen hakies skryf: (3x +/- ? )(x +/-- ?) = 0.

Gebruik dan `n eliminasiemetode waar jy die faktore van 4 gebruik om `n kombinasie te vind wat -11x gee as die resultaat van die vermenigvuldiging. Jy kan óf `n kombinasie van 4 en 1, óf 2 en 2 gebruik, want die vermenigvuldiging van beide getalkombinasies lewer 4. Hou in gedagte dat een van die terme negatief moet wees, want die term is -4.

Probeer (3x +1)(x -4). Wanneer jy dit uitwerk kry jy - 3x -12x +x -4. As jy die terme -12x en x kombineer, kry jy -11x, wat die middelterm is waarby jy wou uitkom. Nou het jy hierdie kwadratiese vergelyking in berekening gebring.

Nog `n voorbeeld; ons probeer om `n vergelyking te faktoriseer wat nie werk nie: (3x-2)(x+2) = 3x +6x -2x -4. As jy hierdie terme kombineer, kry jy 3x -4x -4. Al is die produk van -2 en 2 gelyk aan -4, werk die middelterm nie, want jy het gesoek na -11x, nie -4x nie.

Prent getiteld Los Kwadratiese Vergelykings Stap 3 op

3. Bepaal dat elke paar hakies gelyk is aan nul en behandel hulle as aparte vergelykings. Dit veroorsaak dat jy twee waardes vir x vind wat albei die hele vergelyking gelyk aan nul maak. Noudat jy die vergelyking in berekening gebring het, is al wat oorbly om elke paar hakies gelyk aan nul te maak. So jy kan skryf dat: 3x +1 = 0 en x - 4 = 0.

Prent getiteld Los Kwadratiese Vergelykings Stap 4 op

4. Los elke vergelyking op. In `n kwadratiese vergelyking is daar twee gegewe waardes vir x. Los elke vergelyking afsonderlik op deur die veranderlike te isoleer en skryf die resultate van x neer. Hier is hoe dit gaan:

3x + 1 = 0 =

3x = -1 =

3x/3 = -1/3

x = -1/3

x - 4 = 0

x = 4

x = (-1/3, 4)

Prent getiteld Los Kwadratiese Vergelykings Stap 5 op

5. Kontroleer x = -1/3 duim (3x + 1)(x – 4) = 0:

Ons kry (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... deur:(-1 + 1)(-4 1/3) te vervang ?=? 0 ..... deur te vereenvoudig:(0)(-4 1/3) = 0 ..... deur te vermenigvuldig: dus 0=0 ..... Ja, x = -1/3 werk

Prent getiteld Los Kwadratiese Vergelykings Stap 6 op

6. Kontroleer x = 4 duim (3x + 1)(x - 4) = 0:

Ons kry (3[4] + 1)([4] – 4) ?=? 0..... deur te vervang:(13)(4 – 4) ?=? 0 ..... deur verdof:(13)(0) = 0 ..... deur te vermenigvuldig:0=0 ..... Ja, x = 4 werk

Beide oplossings werk dus afsonderlik en albei word geverifieer as werk en is korrek in twee verskillende oplossings.

Metode 2 van 3: Pas die Abc-formule toe

1. Skuif alle terme na een kant van die vergelyking en voeg die soortgelyke terme saam. Skuif alle terme na die een kant van die gelykheidsteken, en hou die term x positief. Skryf die terme in dalende orde van grootte, dus kom x eerste gevolg deur x, dan die konstante. Hier is hoe om dit te doen:

4x - 5x - 13 =x -5
4x - x - 5x - 13 +5 = 0
3x - 5x - 8 = 0

Prent getiteld Los Kwadratiese Vergelykings Stap 8 op

2. Skryf die abc-formule neer. Dit is: {-b +/-√ (b - 4ac)}/2a

3. Bepaal die waardes van a, b en c in die kwadratiese vergelyking. Die veranderlike a is die koëffisiënt van x, b is die koëffisiënt van x en c is die konstante. Vir die vergelyking 3x -5x - 8 = 0, a = 3, b = -5, en c = -8. Skryf dit neer.

Prent getiteld Los Kwadratiese Vergelykings Stap 9 op

4. Vervang die waardes van a, b en c in die vergelyking. Noudat jy die waardes van die drie veranderlikes ken, kan jy dit net by die vergelyking inprop soos ons hier wys:

{-b +/-√ (b - 4ac)}/2

{-(-5) +/-√ ((-5) - 4(3)(-8))}/2(3) =

{-(-5) +/-√ ((-5) - (-96))}/2(3)

Prent getiteld Los Kwadratiese Vergelykings Stap 11 op

5. Bereken. Nadat u die nommers ingevul het, werk u die probleem verder uit. Hieronder kan jy lees hoe dit verder gaan:

{-(-5) +/-√ ((-5) - (-96))}/2(3) =

{5 +/-√(25 + 96)}/6

{5 +/-√(121)}/6

Prent getiteld Los Kwadratiese Vergelykings Stap 12 op

6. Vereenvoudig die vierkantswortel. As die getal onder die radikale teken `n volmaakte vierkant of ook `n vierkantgetal is, dan kry jy `n heelgetal met die vierkantswortel. In ander gevalle, vereenvoudig die vierkantswortel soveel as moontlik. As die getal negatief is, en jy is seker dat dit die bedoeling is, dan sal die vierkantswortel van die getal minder eenvoudig wees. In hierdie voorbeeld, √(121) = 11. Jy kan dan skryf dat x =(5 +/- 11)/6.

Prent getiteld Los Kwadratiese Vergelykings Stap 13 op

7. Los die positiewe en negatiewe getalle op. Sodra jy van die vierkantswortel ontslae geraak het, kan jy voortgaan totdat jy die negatiewe en positiewe antwoorde vir x kry. Noudat jy (5 +/- 11)/6 het, kan jy die twee moontlikhede neerskryf:

(5 + 11)/6

(5 - 11)/6

Prent getiteld Los Kwadratiese Vergelykings Stap 14 op

8. Los op vir die positiewe en negatiewe antwoorde. Bereken verder:

(5 + 11)/6 = 16/6

(5-11)/6 = -6/6

Prent getiteld Los Kwadratiese Vergelykings Stap 15 op

9. Vereenvoudig. Om dit te vereenvoudig, deel die antwoorde deur die grootste getal wat deur beide die teller en noemer deelbaar is. So deel die eerste breuk deur 2 en die tweede met 6 en jy het x opgelos.

16/6 = 8/3

-6/6 = -1

x = (-1, 8/3)

Metode 3 van 3: Verdeel die vierkant

Prent getiteld Los Kwadratiese Vergelykings Stap 16 op

1. Skuif al die terme na die een kant van die vergelyking. Maak seker dat die a van x is positief. Hier is hoe om dit te doen:

2x - 9 = 12x =
2x - 12x - 9 = 0

In hierdie vergelyking, a gelyk aan 2, b is -12, en c is -9.

Prent getiteld Los Kwadratiese Vergelykings Stap 17 op

2. Beweeg die konstante c na die ander kant toe. Die konstante is die numeriese waarde sonder `n veranderlike. Beweeg dit na die regterkant van die vergelyking:

2x - 12x - 9 = 0

2x - 12x = 9

Prent getiteld Los Kwadratiese Vergelykings Stap 18 op

3. Verdeel die twee kante deur die koëffisiënt van die a of x term. As x geen term voor dit het nie en `n koëffisiënt met die waarde 1 het, kan jy hierdie stap oorslaan. In hierdie geval moet jy alle terme deur 2 deel, soos volg:

2x/2 - 12x/2 = 9/2 =

x - 6x = 9/2

Prent getiteld Los Kwadratiese Vergelykings Stap 19 op

4. Deel b deur twee, vierkantig dit en voeg die resultate by beide kante van die is-teken.Dieb in hierdie voorbeeld is -6. Hier is hoe om dit te doen:

-6/2 = -3 =

(-3) = 9 =

x - 6x + 9 = 9/2 + 9

Prent getiteld Los Kwadratiese Vergelykings Stap 20 op

5. Vereenvoudig beide kante. Faktoreer die terme aan die linkerkant om (x-3)(x-3), of (x-3) te kry. Voeg die terme regs by om 9/2 + 9 te kry, of 9/2 + 18/2, wat optel tot 27/2.

Prent getiteld Los Kwadratiese Vergelykings Stap 21 op

6. Vind die vierkantswortel van beide kante. Die vierkantswortel van (x-3) is eenvoudig (x-3). Jy kan ook die vierkantswortel van 27/2 skryf as ±√(27/2). Daarom, x - 3 = ±√(27/2).

Prent getiteld Los Kwadratiese Vergelykings Stap 22 op

7. Vereenvoudig die vierkantswortel en los op vir x. Om ±√(27/2) te vereenvoudig, soek `n perfekte vierkant of vierkantgetal met die getalle 27 of 2 of in hul faktore. Die vierkant getal 9 kan gevind word in 27, want 9 x 3 = 27. Om 9 van die wortel uit te skakel, skryf dit as `n aparte wortel en vereenvoudig tot 3, die vierkantswortel van 9. Los √3 in die teller van die breuk omdat dit nie as `n faktor van 27 geskei kan word nie, en maak 2 die noemer. Beweeg dan die konstante 3 van die linkerkant van die vergelyking na die regterkant en skryf jou twee oplossings vir x neer:

x = 3 +(√6)/2

x = 3 - (√6)/2)

Wenke

Soos u kan sien, het die radikale teken nie heeltemal verdwyn nie. Daarom word die terme in die teller nie saamgevoeg nie (dit is nie gelyke terme nie). Dit is dus sinloos om die minusse en pluspunte te verdeel. In plaas daarvan, deur te deel, maak ons seker dat elke gemeenskaplike faktor verdwyn - maar "ENIGSTE" as die faktor gelyk is vir beide konstantes, "EN" die koëffisiënt van die vierkantswortel.