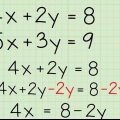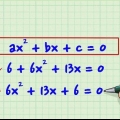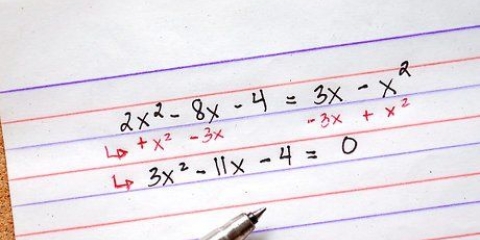Daar is 4 basiese trigonometriese vergelykings: sin x = a; cos x = a bruin x = a; bedjie x = a Die oplossing van die basiese trigonometriese vergelykings word gedoen deur die verskillende posisies van die kromme x op die trigonometriese sirkel te bestudeer en deur `n trigonometriese omskakelingstabel (of sakrekenaar) te gebruik. Om ten volle te verstaan hoe om hierdie en soortgelyke basiese trigonometriese vergelykings op te los, lees die volgende boek:"Trigonometrie: Los trigonometriese vergelykings en ongelykhede op" (Amazon Ebook 2010). Voorbeeld 1. Los op vir sin x = 0,866. Die omskakelingstabel (of sakrekenaar) gee die antwoord: x = Pi/3. Die trigonometriese sirkel gee nog `n kromme (2Pi/3) met dieselfde waarde vir die sinus (0,866). Die trigonometriese sirkel gee ook `n oneindigheid van antwoorde wat uitgebreide antwoorde genoem word. x1 = Pi/3 + 2k.Pi, en x2 = 2Pi/3.(Antwoorde binne `n tydperk (0, 2Pi)) x1 = Pi/3 + 2k Pi, en x2 = 2Pi/3 + 2k Pi.(Gedetailleerde antwoorde). Voorbeeld 2. Los op: cos x = -1/2. Sakrekenaars gee x = 2 Pi/3. Die trigonometriese sirkel gee ook x = -2Pi/3. x1 = 2Pi/3 + 2k.Pi, en x2 = - 2Pi/3.(Antwoorde vir periode (0, 2Pi)) x1 = 2Pi/3 + 2k Pi, en x2 = -2Pi/3 + 2k.PI.(Gedetailleerde antwoorde) Voorbeeld 3. Los op: bruin (x - Pi/4) = 0. x = Pi/4 ;(Antwoord) x = Pi/4 + k Pi;(Uitgebreide antwoord) Voorbeeld 4. Los op: bed 2x = 1.732. Sakrekenaars en die trigonometriese sirkel gee: x = Pi/12 ;(Antwoord) x = Pi/12 + k Pi ;(Gedetailleerde antwoorde) 
Om `n gegewe trigonometriese vergelyking na standaard trigonometriese vergelykings om te skakel, gebruik standaard algebraïese omskakelings (faktoriseer, gemene faktor, polinome...), definisies en eienskappe van trigonometriese funksies en trigonometriese identiteite. Daar is ongeveer 31, waarvan 14 trigonometriese identiteite is, van 19 tot 31, ook genoem detransformeer identiteite, omdat hulle gebruik word in die omskakeling van trigonometriese vergelykings. Sien bogenoemde boek. Voorbeeld 5: Die trigonometriese vergelyking: sin x + sin 2x + sin 3x = 0 kan met behulp van trigonometriese identiteite omgeskakel word in `n produk van basiese trigonometriese vergelykings: 4cos x*sin (3x/2)*cos (x/2) = 0. Die basiese trigonometriese vergelykings om op te los is: cos x = 0 ; sin(3x/2) = 0 ; en cos(x/2) = 0. 
Voordat jy kan leer hoe om trigonometriese vergelykings op te los, moet jy weet hoe om vinnig die krommes te vind waarvan die trigonometriese funksies bekend is. Omskakelingswaardes van krommes (of hoeke) kan met trigonometriese tabelle of die sakrekenaar bepaal word. Voorbeeld: Los op vir cos x = 0.732. Die sakrekenaar gee die oplossing x = 42.95 grade. Die eenheidsirkel gee ander krommes met dieselfde waarde vir die cosinus. 
Jy kan `n grafiek maak om die oplossing vir die eenheidsirkel te illustreer. Die eindpunte van hierdie krommes bestaan uit gewone veelhoeke op die trigonometriese sirkel. Enkele voorbeelde: Die eindpunte van die kromme x = Pi/3 + k.Pi/2 is `n vierkant op die eenheidsirkel. Die krommes van x = Pi/4 + k.Pi/3 word voorgestel deur die koördinate van `n seshoek op die eenheidsirkel. 
As die gegewe trigonometriese vergelyking slegs een trigonometriese funksie bevat, los dit op as `n standaard trigonometriese vergelyking. As die gegewe vergelyking twee of meer trigonometriese funksies bevat, dan is daar 2 metodes van oplossing afhangende van die opsies vir die omskakeling van die vergelyking. a.Metode 1. Skakel die trigonometriese vergelyking om in `n produk van die vorm: f(x).g(x) = 0 of f(x).g(x).h(x) = 0, waar f(x), g(x) en h(x) basiese trigonometriese vergelykings is. Voorbeeld 6. Los op: 2cos x + sin 2x = 0.(0 < X < 2Pi) Oplossing. Vervang sin 2x in die vergelyking deur die identiteit te gebruik: sin 2x = 2*sin x*cos x. cos x + 2*sin x*cos x = 2cos x*( sin x + 1)= 0. Los dan 2 standaard trigonometriese funksies op: cos x = 0, en (sin x + 1) = 0. Voorbeeld 7. Los op: cos x + cos 2x + cos 3x = 0.(0 < X < 2Pi) Oplossing: Skakel dit om na `n produk deur die trigonometriese identiteite te gebruik: cos 2x(2cos x + 1 ) = 0. Los nou die 2 basiese trigonometriese vergelykings op: cos 2x = 0, en (2cos x + 1) = 0. Voorbeeld 8. Los op: sin x - sin 3x = cos 2x.(0 < X < 2Pi) Oplossing: Skakel dit om na `n produk deur die trigonometriese identiteite te gebruik: -cos 2x*(2sin x + 1) = 0. Los nou die 2 basiese trigonometriese vergelykings op: cos 2x = 0, en (2sin x + 1) = 0. B.Benadering 2. Skakel die trigonometriese vergelyking om na `n trigonometriese vergelyking met slegs een unieke trigonometriese funksie as `n veranderlike. Daar is `n paar wenke oor hoe om `n geskikte veranderlike te kies. Algemene veranderlikes is: sin x = t; cos x = t; cos 2x = t, tan x = t en tan (x/2) = t. Voorbeeld 9. Los op: 3sin^2 x - 2cos^2 x = 4sin x + 7(0 < X < 2Pi). Oplossing. In die vergelyking, vervang (cos^2 x) met (1 - sin^2 x), en vereenvoudig die vergelyking: 3sin^2 x - 2 + 2sin^2 x - 4sin x - 7 = 0. Gebruik nou sin x = t. Die vergelyking word: 5t^2 - 4t - 9 = 0. Dit is `n kwadratiese vergelyking met 2 wortels: t1 = -1 en t2 = 9/5. Ons kan die tweede t2 verwerp omdat > 1. Los nou op vir: t = sin = -1 --> x = 3Pi/2. Voorbeeld 10. Los op: bruin x + 2 bruin^2 x = kot x + 2. Oplossing. Gebruik tan x = t. Skakel die gegewe vergelyking om in `n vergelyking met t as die veranderlike: (2t + 1)(t^2 - 1) = 0. Los op vir t uit hierdie produk, los dan die standaard trigonometriese vergelyking op tan x = t vir x. 
Daar is `n paar spesiale trigonometriese vergelykings wat `n paar spesifieke omskakelings vereis. Voorbeelde: a*sin x+ b*cos x = c ; a(sin x + cos x) + b*cos x*sin x = c ; a*sin^2 x + b*sin x*cos x + c*cos^2 x = 0 
Alle trigonometriese funksies is periodiek, wat beteken dat hulle terugkeer na dieselfde waarde na `n rotasie oor `n tydperk. Voorbeelde: Die funksie f(x) = sin x het 2Pi as periode. Die funksie f(x) = tan x het Pi as punt. Die funksie f(x) = sin 2x het Pi as punt. Die funksie f(x) = cos (x/2) het 4Pi as periode. As die periode in die oefeninge/toets gespesifiseer word, hoef jy net die kromme(s) x binne hierdie tydperk te vind. WAARSKUWING: Om trigonometriese vergelykings op te los is moeilik en lei dikwels tot foute en foute. Daarom moet antwoorde noukeurig nagegaan word. Nadat u dit opgelos het, kan u die antwoorde nagaan deur `n grafiese sakrekenaar te gebruik, vir `n direkte voorstelling van die gegewe trigonometriese vergelyking R(x) = 0. Die antwoorde (as `n vierkantswortel) word in desimale gegee. As `n voorbeeld, Pi het `n waarde van 3.14
Los trigonometriese vergelykings op
`n Trigonometriese vergelyking is `n vergelyking met een of meer trigonometriese funksies van die veranderlike trigonometriese kromme x. Om vir x op te los beteken om die waardes van die trigonometriese krommes te vind waarvan die trigonometriese funksies die trigonometriese vergelyking waar maak.
- Antwoorde of waardes van die oplossingskrommes word uitgedruk in grade of radiale. Voorbeelde:
x = Pi/3 ; x = 5Pi/6 ; x = 3Pi/2 ; x = 45 grade; x = 37.12 grade; x = 178.37 grade
- Let wel: Op die eenheidsirkel is die trigonometriese funksies van enige kromme gelyk aan die trigonometriese funksies van die ooreenstemmende hoek. Die eenheidsirkel definieer alle trigonometriese funksies van die veranderlike kromme x. Dit word ook as bewys gebruik wanneer basiese trigonometriese vergelykings en ongelykhede opgelos word.
- Voorbeelde van trigonometriese vergelykings:
- sin x + sin 2x = 1/2; tan x + bed x = 1.732;
- cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1 .
- Die eenheidsirkel.
- Dit is `n sirkel met Radius = 1, waar O die oorsprong is. Die eenheidsirkel definieer 4 trigonometriese hooffunksies van die veranderlike kromme x, wat antikloksgewys rondom dit sirkel.
- Wanneer die kromme met waarde x op die eenheidsirkel verskil, geld dan:
- Die horisontale as OAx definieer die trigonometriese funksie f(x) = cos x.
- Die vertikale as OBy definieer die trigonometriese funksie f(x) = sin x.
- Die vertikale as AT definieer die trigonometriese funksie f(x) = tan x.
- Die horisontale as BU definieer die trigonometriese funksie f(x) = cot x.
- Die eenheidsirkel word ook gebruik om basiese trigonometriese vergelykings en standaard trigonometriese ongelykhede op te los, deur die verskillende posisies van die kromme x op die sirkel te oorweeg.
Trappe

1. Verstaan die oplossingsmetode.
- Om `n trigonometriese vergelyking op te los, skakel dit om in een of meer basiese trigonometriese vergelykings. Die oplossing van trigonometriese vergelykings lei uiteindelik tot die oplossing van 4 basiese trigonometriese vergelykings.

2. Weet hoe om basiese trigonometriese vergelykings op te los.

3. Leer die transformasies wat gebruik word om trigonometriese vergelykings op te los.

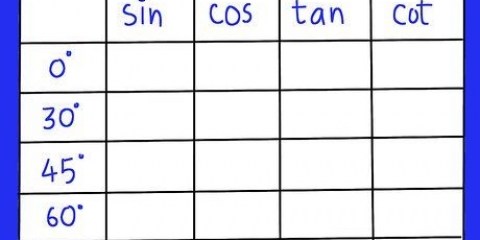
4. Vind die krommes waarvan die trigonometriese funksies bekend is.

5. Teken die boog van die antwoord op die eenheidsirkel.

6. Leer hoe om trigonometriese vergelykings op te los.

7. Los spesiale trigonometriese vergelykings op.

8. Leer die periodieke eienskappe van trigonometriese funksies.
Artikels oor die onderwerp "Los trigonometriese vergelykings op"
Оцените, пожалуйста статью
Gewilde