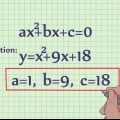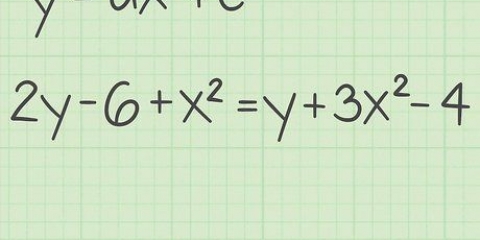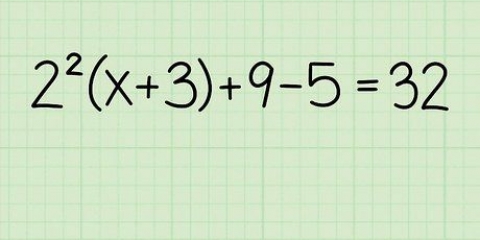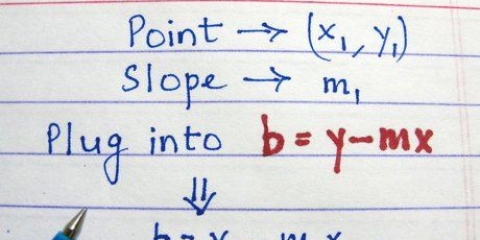Los 'n kubieke vergelyking op

Inhoud

Trappe

Die eerste keer dat jy `n kubieke vergelyking (van die vorm byl + bx + cx + d=0) dit kan amper onoplosbaar lyk. Hierdie metode om kubieke vergelykings op te los, bestaan egter al eeue lank! Dit is in die 16de eeu deur die Italiaanse wiskundiges Niccolò Tartaglia en Gerolamo Cardano ontdek. Dit was een van die eerste formules wat aan die antieke Grieke en Romeine onbekend was. Om kubieke vergelykings op te los kan baie moeilik wees, maar met die regte benadering (en genoeg basiese kennis), kan selfs die moeilikste kubieke vergelykings getem word.

Trappe

Metode 1 van 3: Los dit op met die abc-formule

Prent getiteld Los `n kubieke vergelyking op Stap 1

1. Kyk of die kubieke vergelyking `n konstante bevat. Soos hierbo aangedui, het kubieke vergelykings die vorm byl + bx + cx + d=0. b, c, en d kan 0 wees sonder om te verander of dit `n kubieke vergelyking is of nie - dit beteken in wese dat `n vergelyking nie uit alle terme hoef te bestaan nie bx, cx of d om `n kubieke vergelyking te wees. Jy begin hierdie relatief eenvoudige metode om kubieke vergelykings op te los toepas deur eers te kyk of jou vergelyking `n konstante (a d-waar die). Is dit nie die geval nie, dan kan jy de abc formule om die antwoorde van die vergelyking met `n bietjie wiskunde te vind.

As die vergelyking wel `n konstante bevat, sal jy `n ander metode moet gebruik. Sien hieronder vir alternatiewe benaderings.

Prent getiteld Los `n kubieke vergelyking op Stap 2

2. ontbind a X uit die vergelyking. Aangesien jou vergelyking nie `n konstante bevat nie, het elke term in die vergelyking `n X-veranderlike. Dit beteken dat a X kan uit die vergelyking in berekening gebring word om dit te vereenvoudig. Doen dit en herskryf jou vergelyking in die vorm X(byl + bx + c).

Gestel jy het byvoorbeeld die vergelyking 3X + -2X + 14X=0. Deur a X buite hakies, kry ons X(3X + -2X + 14)=0.

Prent getiteld Los `n kubieke vergelyking op Stap 3

3. Gebruik die abc-formule om die terme tussen hakies op te los. Jy het dalk opgemerk dat die terme van jou nuwe vergelyking tussen hakies in die vorm van `n kwadratiese vergelyking (byl + bx + c). Dit beteken dat ons die waardes kan vind waarvoor die kwadratiese vergelyking gelyk is aan nul a, b en c in die abc-formule ({-b +/-√ (b- 4ac)}/2a). Dit sal twee van die antwoorde van jou kubieke vergelyking vind.

In ons voorbeeldstelling vul ons ons waardes in a, b en c (onderskeidelik 3, -2 en 14) in die kwadratiese vergelyking in:

{-b +/-√ (b- 4ac)}/2a

{-(-2) +/-√ ((-2)-4(3)(14))}/2(3)

{2 +/-√ (4 - (12)(14))}/6

{2 +/-√ (4 - (168)}/6

{2 +/-√ (-164)}/6

Antwoord 1:

{2 + √(-164)}/6

{2 + 12.8i}/6

Antwoord 2:

{2 - 12.8i}/6

Prent getiteld Los `n kubieke vergelyking op Stap 4

4. Gebruik nul en die kwadratiese antwoorde as antwoorde vir jou kubieke vergelyking. Vierhoeksvergelykings het twee oplossings, maar kubieke vergelykings het drie. Jy het reeds twee - dit is die antwoorde wat jy gevind het deur die "kwadratiese vergelyking" tussen hakies uit te werk. In daardie gevalle waar `n vergelyking gepas is vir hierdie `buite hakies`, sal die derde antwoord altyd wees 0 is. Baie geluk - jy het sopas `n kubieke vergelyking opgelos.

Die rede waarom dit werk, het te make met die fundamentele feit dat enige getal vermenigvuldig met nul is gelyk aan nul. Wanneer jy die vergelyking omskakel na die vorm X(byl + bx + c)=0, jy verdeel in wese die twee in dele: een deel is die X-veranderlike buite hakies en die ander is die vierkant binne hakies. As enige van hierdie dele gelyk is aan nul, dan is die hele vergelyking ook. Dus as die twee antwoorde op die vierkant binne die hakies daardie deel nul maak, dan sal die antwoorde op die kubieke vergelyking ook die deel buite die hakies gelyk aan nul maak.

Metode 2 van 3: Los op deur lyste faktore te gebruik

Prent getiteld Los `n kubieke vergelyking op Stap 5

1. Maak seker dat jou kubieke vergelyking `n konstante het. Alhoewel die bogenoemde metode nuttig is omdat dit nie vereis dat jy nuwe wiskundevaardighede aanleer nie, sal dit nie altyd werk om kubieke vergelykings op te los nie. As jou vergelyking in die vorm is byl + bx + cx + d=0 toestand, en d nie-nul is nie, sal die hakies nie werk nie, en jy sal óf hierdie metode óf die een in die volgende deel nodig hê.

Gestel jy het byvoorbeeld die gegewe vergelyking 2X + 9X + 13X=-6. In hierdie geval sal `n 0 aan die regterkant van die gelykheidsteken vereis dat 6 aan beide kante bygevoeg word. Ons nuwe vergelyking is 2X + 9X + 13X + 6=0, d=6, dus kan ons nie die hakies van die vorige deel gebruik nie.

Prent getiteld Los `n kubieke vergelyking op Stap 6

2. Bepaal die faktore van a en d. Om die kubieke vergelyking op te los, begin deur die faktore van te bepaal a (die koëffisiënt van die X terme d (die konstante aan die einde van die vergelyking). Ter herinnering, faktore is daardie getalle wat vermenigvuldig saam `n ander getal vorm. Byvoorbeeld, omdat jou 6 uit die vermenigvuldiging 6 ontstaan &tyd; 1 en 2 × 3, is 1, 2, 3 en 6 faktore van 6.

In ons voorbeeldstelling, a=2 en d=6. Die faktore van 2 is 1 en 2. Die faktore van 6 is 1, 2, 3 en 6.

Prent getiteld Los `n kubieke vergelyking op Stap 7

3. Deel die faktore van a deur die faktore van d. Nou lys jy al die waardes wat jy kry deur elke faktor te deel a deur enige faktor d. Dit lei gewoonlik tot baie breuke en `n paar heelgetalle. Die heelgetaloplossings van jou kubieke vergelyking sal óf een van die heelgetalle uit die lys wees óf die negatiewe getal van een van hierdie getalle.

In ons vergelyking bereken jy die faktore van a (1, 2) oor die faktore van d (1, 2, 3, 6) en jy kry die volgende lys: 1, 1/2, 1/3, 1/6, 2 en 2/3. Nou voeg ons die negatiewe getalle by die lys om dit volledig te maak: 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 en -2/3. Die heelgetaloplossing van ons kubieke vergelyking kan iewers in hierdie lys gevind word.

Prent getiteld Los `n kubieke vergelyking op Stap 8

4. Gebruik sintetiese deling om jou antwoorde handmatig na te gaan. Sodra jy die lys waardes saamgestel het, kan jy die heelgetaloplossings vir jou kubieke vergelyking vind deur elke heelgetal vinnig met die hand in te voer en te kontroleer watter gelyk aan nul is. As jy nie tyd hieraan wil spandeer nie, is daar `n effens vinniger metode volgens `n tegniek genaamd sintetiese deel. Die kern is dat jy heelgetalle deur die oorspronklike deel a, b, c en d koëffisiënte van jou kubieke vergelyking. As jy oorbly met `n res van 0, is jou waarde een van die oplossings van die kubieke vergelyking.

Sintetiese deel is `n komplekse onderwerp - volg die skakel hierbo vir meer inligting. Hier is `n voorbeeld van die vind van een van die oplossings vir ons kubieke vergelyking deur sintetiese deling te gebruik:

-1 | 2 9 13 6

__| -2-7-6

__| 2 7 6 0

Aangesien ons eindig met `n 0 as res, weet ons dat een van die oplossings van ons kubieke vergelyking die heelgetal is -1 is.

Metode 3 van 3: Gebruik die `diskriminant`

Prent getiteld Los `n kubieke vergelyking op Stap 9 op

1. Skryf die waardes van a, b, c en d. In hierdie metode om die oplossings van `n kubieke vergelyking te vind, sal ons sterk staatmaak op die koëffisiënte van die terme in ons vergelyking. Om hierdie rede is dit wys om die terme te gebruik a, b, c en d skryf dit neer voor jy begin sodat jy nie vergeet wat elkeen is nie.

Byvoorbeeld, vir die vergelyking X - 3X + 3X - 1, ons skryf a=1, b=-3, c=3 en d=-1. Moenie vergeet dat van `n X-veranderlike sonder koëffisiënt word aanvaar dat die koëffisiënt gelyk is aan 1.

Prent getiteld Los `n kubieke vergelyking op Stap 10 op

2. Bereken Δ0=b - 3ac. Wanneer jy die diskriminant gebruik om kubieke vergelykings op te los, het jy `n bietjie meer gevorderde wiskunde nodig, maar as jy die prosedure noukeurig volg, sal jy vind dat dit `n waardevolle hulpmiddel is om daardie reeds moeilike kubieke vergelykings op te los. Begin deur Δ0 te vind, die eerste van verskeie belangrike waardes wat ons benodig, deur die toepaslike waardes in die formule te vervang b - 3ac.

In ons voorbeeldprobleem los ons dit soos volg op:

b - 3ac

(-3) - 3(1)(3)

9 - 3(1)(3)

9 - 9=0=Δ0

Prent getiteld Los `n kubieke vergelyking op Stap 11 op

3. Bereken Δ1=2b - 9ABC + 27ad. Die volgende belangrike hoeveelheid wat ons benodig, Δ1, verg `n bietjie meer werk, maar kan op baie dieselfde manier gevind word as Δ0. Vervang die korrekte waardes in die formule 2b - 9ABC + 27ad vir die waarde van Δ1.

In ons voorbeeldprobleem los ons dit soos volg op:

2(-3) - 9(1)(-3)(3) + 27(1)(-1)

2(-27) - 9(-9) + 27(-1)

-54 + 81 - 27

81 - 81=0=Δ1

Prent getiteld Los `n kubieke vergelyking Stap 12 op

4. Bereken Δ=Δ1 - 4Δ0) ÷ -27a. Dan bereken ons die diskriminant van die kubieke vergelyking van die waardes vir Δ0 en Δ1. `n Diskriminant is bloot `n getal wat vir ons iets vertel oor die antwoorde van `n polinoom (onbewustelik ken jy dalk reeds die kwadratiese diskriminant: b - 4ac). In die geval van die kubieke vergelyking, as die diskriminant positief is, dan het die vergelyking drie reële oplossings. As die diskriminant nul is, dan het die vergelyking een of twee werklike oplossings, en sommige van daardie oplossings word gedeel. As dit negatief is, het die vergelyking net een oplossing. (`n Kubieke vergelyking het altyd een werklike oplossing, want die grafiek is altyd ten minste een keer met die X-as snye.)

In ons voorbeeldprobleem is die bepaling van Δ baie eenvoudig, want beide Δ0 en Δ1=0. Ons los dit soos volg op:

Δ1 - 4Δ0) ÷ -27a

(0) - 4(0)) -27(1)

0 - 0 27

0=Δ, dus het ons vergelyking 1 of 2 antwoorde.

Prent getiteld Los `n kubieke vergelyking op Stap 13

5. bereken C=√(√((Δ1 - 4Δ0) + Δ1)/ 2). Die laaste belangrike waarde om te bereken is C. Met hierdie belangrike hoeveelheid kan ons uiteindelik die drie oplossings vind. Los dit op soos gewoonlik deur Δ1 en Δ0 te vervang waar nodig.

In ons voorbeeldprobleem vind ons C soos volg:

√(√((Δ1 - 4Δ0) + Δ1)/ 2)

√(√((0 - 4(0)) + (0))/ 2)

√(√((0 - 0) + (0))/ 2)

0=C

Prent getiteld Los `n kubieke vergelyking op Stap 14 op

6. Bereken die drie antwoorde met jou veranderlikes. Die antwoorde op jou kubieke vergelyking word deur die formule gegee (b + uC + (Δ0/uC)) / 3a, waardeur jy=(-1 + √(-3))/2 en n is 1, 2 of 3. Voer jou waardes in waar nodig om dit op te los - dit verg baie wiskunde, maar behoort jou drie moontlike antwoorde te gee!

In ons voorbeeldprobleem kan ons dit oplos deur die antwoord na te gaan wanneer n gelyk is aan 1, 2 of 3. Die antwoorde wat ons uit hierdie toetse kry, is die moontlike antwoorde vir ons kubieke vergelyking - enige oplossing wat 0 oplewer na vervanging in die vergelyking is korrek. Gestel ons kry byvoorbeeld 1 in antwoord op een van die toetse, want die invoer van 1 in X - 3X + 3X - 1 lei tot 0 as antwoord, dan 1 een van die antwoorde op ons kubieke vergelyking.