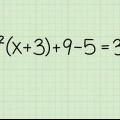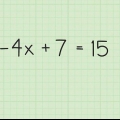Die gebruik van die verspreidingseienskap om 'n vergelyking op te los

Inhoud

Trappe
Wenke

Die distributiewe eienskap is `n reël in wiskunde vir die vereenvoudiging van `n vergelyking met hakies. Jy het waarskynlik vroeg geleer dat jy eers die bewerkings tussen hakies moet doen, maar met algebraïese uitdrukkings is dit nie altyd moontlik nie. Die distributiewe eienskap laat jou toe om die term buite hakies te vermenigvuldig met die terme daarin. Jy moet versigtig wees dat jy dit op die regte manier doen, anders kan jy inligting verloor en die vergelyking is nie meer korrek nie. Jy kan ook die distributiewe eienskap gebruik om vergelykings met breuke te vereenvoudig.

Trappe

Metode 1 van 4: Gebruik die Fundamentele Verspreidende Eiendom

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 1

1. Vermenigvuldig die term buite hakies met enige term binne hakies. Om dit te doen, verdeel jy in wese die buitenste term onder die innerlike terme. Vermenigvuldig die term buite hakies met die eerste term binne hakies. Dan vermenigvuldig jy dit met die tweede term. As daar meer as twee terme is, gaan voort om die term buite hakies oor alle terme binne die hakies te versprei. Los net die operateurs (plus of minus) binne die hakies.

$2 (X - 3) = 10$ $2(x-3)=10$
$2 (X) - (2) (3) = 10$ $2(x)-(2)(3)=10$
$2 X - 6 = 10$ $2x-6=10$

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 2

2. Kombineer soortgelyke terme. Voordat jy die vergelyking kan oplos, moet jy soortgelyke terme kombineer. Kombineer alle numeriese terme met mekaar. Daarbenewens kombineer jy alle veranderlike terme afsonderlik. Om die vergelyking te vereenvoudig, orden die terme so dat die veranderlikes aan die een kant van die gelykteken is en die konstantes (slegs die getalle) aan die ander kant.

2 X - 6 = 10

$2x-6=10$ ....(oorspronklike probleem)

2 X - 6 (+ 6) = 10 (+ 6)

$2x-6(+6)=10(+6)$ .... (voeg 6 by aan beide kante)

2 X = 16

$2x=16$ .... (Veranderlike links; konstant regs)

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 3

3. Los die vergelyking op. los

X

$X$ deur beide kante van die vergelyking te deel deur die koëffisiënt vir die veranderlike.

2 X = 16

$2x=16$ ....(oorspronklike probleem)

2 X / 2 = 16 / 2

$2x/2=16/2$ ....(deel beide kante deur 2)

X = 8

$x=8$ ....(oplossing)

Metode 2 van 4: Verdeel negatiewe koëffisiënte

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 4

1. Verdeel `n negatiewe getal saam met die minusteken. As jy `n term of terme tussen hakies met `n negatiewe getal gaan vermenigvuldig, maak seker dat jy die minusteken op elke term binne die hakies toepas.

Onthou die basiese reëls vir vermenigvuldiging met negatiewe getalle:

Minus x Minus = Plus.
Minus x Plus = Minus.

Kyk na die volgende voorbeeld:

- 4 (9 - 3 X) = 48

$-4(9-3x)=48$ .... (oorspronklike probleem)

- 4 (9) - (- 4) (3 X) = 48

$-4(9)-(-4)(3x)=48$ ....(vermenigvuldig -4 met elke term)

- 36 - (- 12 X) = 48

$-36-(-12x)=48$ ....(vereenvoudig die vermenigvuldiging)

- 36 + 12 X = 48

$-36+12x=48$ ....(let op dat `minus -12` dieselfde is as +12)

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 5

2. Kombineer soortgelyke terme. Nadat jy die verdeling voltooi het, moet jy die vergelyking vereenvoudig deur alle veranderlike terme na die een kant van die gelyke teken te skuif, en alle getalle sonder veranderlikes na die ander kant. Jy doen dit deur middel van `n kombinasie van optel of aftrek.

- 36 + 12 X = 48

$-36+12x=48$ ....(oorspronklike probleem)

- 36 (+ 36) + 12 X = 48 + 36

$-36(+36)+12x=48+36$ ....(voeg 36 by aan elke kant)

12 X = 84

$12x=84$ ....(vereenvoudig die byvoeging om die veranderlike te isoleer)

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 6

3. Deel om die finale oplossing te kry. Los die vergelyking op deur beide kante van die vergelyking te deel deur die koëffisiënt van die veranderlike. Dit moet lei tot `n enkele veranderlike aan die een kant van die vergelyking, met die resultaat aan die ander kant.

12 X = 84

$12x=84$ ....(oorspronklike probleem)

12 X / 12 = 84 / 12

$12x/12=84/12$ ....(deel beide kante deur 12)

X = 7

$x=7$ ....(oplossing)

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 7

4. Behandel aftrekking as optelling (van -1). Wanneer jy `n minusteken in `n algebra-probleem sien, veral as dit voor `n hakies is, sê dit in wese + (-1). Dit help om die minusteken behoorlik oor alle terme tussen hakies te versprei. Los dan die probleem op soos voorheen.

Oorweeg byvoorbeeld die probleem,

4 X - (X + 2) = 4

$4x-(x+2)=4$ . Om seker te maak dat jy die minusteken behoorlik versprei het, herskryf die probleem soos volg:

4 X + (- 1) (X + 2) = 4

$4x+(-1)(x+2)=4$

Dan versprei jy -1 oor die terme tussen hakies, soos volg:

4 X + (- 1) (X + 2) = 4

$4x+(-1)(x+2)=4$ ....(gewysigde kwessie)

4 X - X - 2 = 4

$4x-x-2=4$ ....(vermenigvuldig -1 met x en met 2)

3 X - 2 = 4

$3x-2=4$ ....(kombineer terme)

3 X - 2 + 2 = 4 + 2

$3x-2+2=4+2$ ....(voeg 2 by aan beide kante)

3 X = 6

$3x=6$ ....(vereenvoudig terme)

3 X / 3 = 6 / 3

$3x/3=6/3$ ....(deel beide kante deur 3)

X = 2

$x=2$ ....(oplossing)

Metode 3 van 4: Gebruik die distributiewe eienskap om breuke te vereenvoudig

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 8

1. Vind uit of daar breukkoëffisiënte of konstantes is. Soms moet jy dalk `n probleem oplos met breuke as koëffisiënte of konstantes. Jy kan hulle los soos hulle is en die fundamentele reëls van algebra op hulle toepas om die probleem op te los. Deur die distributiewe eienskap te gebruik, kan jy egter dikwels die oplossing vereenvoudig deur die breuke na heelgetalle om te skakel.

Kyk na die volgende voorbeeld $X - 3 = \frac{X}{3} + \frac{1}{6}$ $x-3={frac{x}{3}}+{frac{1}{6}}$ . Die breuke in hierdie voorbeeld is $\frac{X}{3}$ ${frac{x}{3}}$ en $\frac{1}{6}$ ${frac{1}{6}}$ .

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 9

2. Vind die kleinste gemene veelvoud (GKM) vir alle noemers. By hierdie stap kan jy alle heelgetalle ignoreer. Kyk net na die breuke en bepaal die LCF vir alle noemers. Bepaal die kgf deur te soek na die kleinste getal wat `n veelvoud is van die noemers van beide breuke in die vergelyking. In hierdie voorbeeld is die noemers 3 en 6, so 6 is die kgf.

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 10

3. Vermenigvuldig alle terme van die vergelyking met die kgf. Onthou, jy kan enige bewerking op `n wiskundevergelyking toepas, solank jy dit aan beide kante doen. Deur elke term van die vergelyking met die lcg te vermenigvuldig kanselleer die terme mekaar uit en `word` heelgetalle. Plaas jou hakies om die hele linker- en regterkant van die vergelyking en doen dan die verspreiding:

X - 3 = \frac{X}{3} + \frac{1}{6}

$x-3={frac{x}{3}}+{frac{1}{6}}$ ....(oorspronklike vergelyking)

(X - 3) = (\frac{X}{3} + \frac{1}{6})

$(x-3)=({frac{x}{3}}+{frac{1}{6}})$ ....(pas hakies toe)

6 (X - 3) = 6 (\frac{X}{3} + \frac{1}{6})

$6(x-3)=6({frac{x}{3}}+{frac{1}{6}})$ ....(vermenigvuldig beide kante met die kgf)

6 X - 6 (3) = 6 (\frac{X}{3}) + 6 (\frac{1}{6})

$6x-6(3)=6({frac{x}{3}})+6({frac{1}{6}})$ ....(verspreide vermenigvuldiging)

6 X - 18 = 2 X + 1

$6x-18=2x+1$ ....(vereenvoudig vermenigvuldiging)

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 11

4. Kombineer soortgelyke terme. Kombineer alle terme sodat alle veranderlikes aan die een kant van die vergelyking is en alle konstantes aan die ander kant. Gebruik die basiese optel- en aftrekbewerkings om terme van die een kant van die vergelyking na die ander te skuif.

6 X - 18 = 2 X + 1

$6x-18=2x+1$ ....(vereenvoudigde probleem)

6 X - 2 X - 18 = 2 X - 2 X + 1

$6x-2x-18=2x-2x+1$ ....(trek 2x van beide kante af)

4 X - 18 = 1

$4x-18=1$ ....(vereenvoudig minus som)

4 X - 18 + 18 = 1 + 18

$4x-18+18=1+18$ ....(voeg 18 by aan beide kante)

4 X = 19

$4x=19$ ....(vereenvoudig optelling)

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 12

5. Los die vergelyking op. Vind die finale oplossing deur beide kante van die vergelyking te deel deur die koëffisiënt van die veranderlike. Dit laat jou met x aan die een kant van die vergelyking en die numeriese oplossing aan die ander kant.

4 X = 19

$4x=19$ ....(pasgemaakte kwessie)

4 X / 4 = 19 / 4

$4x/4=19/4$ ....(deel beide kante deur 4)

X = \frac{19}{4} of 4 \frac{3}{4}

$x={frac{19}{4}}{text{ of }}4{frac{3}{4}}$ ....(finale oplossing)

Metode 4 van 4: Verdeel `n breuk met `n vergelyking

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 13

1. Interpreteer `n breuk met `n vergelyking as `n verspreide deling. Soms sien jy `n probleem met veelvuldige terme in die teller van `n breuk, bo `n gemene deler. Jy moet dit as `n distributiewe probleem hanteer en die noemer op elke term van die teller toepas. Jy kan die breuk herskryf om die verspreiding te wys. Soos volg:

$4 X + 8 2 = 4$ ${frac{4x+8}{2}}=4$ .....(oorspronklike probleem)
$4 X 2 + \frac{8}{2} = 4$ ${frac{4x}{2}}+{frac{8}{2}}=4$ .....(vermenigvuldig die noemer met elke term van die teller)

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 14

2. Vereenvoudig elke teller as aparte breuk. Nadat u die deler oor elke kwartaal versprei het, kan u elke term individueel vereenvoudig.

4 X 2 + \frac{8}{2} = 4

${frac{4x}{2}}+{frac{8}{2}}=4$ .....(pasgemaakte kwessie)

2 X + 4 = 4

$2x+4=4$ .....(vereenvoudig die breuke)

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 15

3. Isoleer die veranderlike. Gaan voort om die probleem op te los deur die veranderlike aan die een kant van die vergelyking te isoleer en die konstante terme na die ander kant te skuif. Doen dit deur `n kombinasie van optel en aftrek, waar nodig.

2 X + 4 = 4

$2x+4=4$ .....(pasgemaakte kwessie)

2 X + 4 - 4 = 4 - 4

$2x+4-4=4-4$ .....(trek 4 van beide kante af)

2 X = 0

$2x=0$ .....(isoleer x aan die een kant)

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 16

4. Deel deur die koëffisiënt om die probleem op te los. In die laaste stap deel jy deur die koëffisiënt van die veranderlike. Dit gee die finale oplossing, met die enkele veranderlike aan die een kant van die vergelyking en die numeriese oplossing aan die ander kant.

2 X = 0

$2x=0$ .....(pasgemaakte kwessie)

2 X / 2 = 0 / 2

$2x/2=0/2$ .....(deel beide kante deur 2)

X = 0

$x=0$ .....(oplossing)

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 17

5. Vermy die algemene fout om net een term te deel. Dit is aanloklik (maar verkeerd) om die eerste term van die teller deur die noemer te deel en die breuk uit te skakel. `n Fout soos hierdie sal so lyk vir die bogenoemde probleem:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(oorspronklike probleem)

2 X + 8 = 4

$2x+8=4$ .....(slegs 4x word deur 2 gedeel, in plaas van die volle teller)

2 X + 8 - 8 = 4 - 8

$2x+8-8=4-8$

2 X = - 4

$2x=-4$

X = - 2

$x=-2$ ..... (verkeerde oplossing)

Prent getiteld Gebruik Verspreidende Eiendom om `n vergelyking op te los Stap 18

6. Kontroleer die korrektheid van jou oplossing. Jy kan altyd jou werk nagaan deur jou oplossing in die oorspronklike probleem in te voeg. Wanneer jy wil vereenvoudig, moet jy by `n ware stelling uitkom. As jy vereenvoudig en `n verkeerde stelling as antwoord kry, dan is jou oplossing verkeerd. In hierdie voorbeeld toets jy die twee oplossings vir x = 0 en x =-2 om te sien watter een korrek is.

Begin met oplossing x=0:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(oorspronklike probleem)

4 (0) + 8 2 = 4

${frac{4(0)+8}{2}}=4$ .....(vervang 0 vir x)

0 + 8 2 = 4

${frac{0+8}{2}}=4$

\frac{8}{2} = 4

${frac{8}{2}}=4$

4 = 4

$4=4$ .....(Waar. Dit is die regte oplossing.)

Probeer die `verkeerde oplossing vir x=-2:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(oorspronklike probleem)

4 (- 2) + 8 2 = 4

${frac{4(-2)+8}{2}}=4$ .....(tik -2 vir x)

- 8 + 8 2 = 4

${frac{-8+8}{2}}=4$

\frac{0}{2} = 4

${frac{0}{2}}=4$

0 = 4

$0=4$ .....(Verkeerde stelling. Daarom is x=-2 onwaar.)

Wenke

Jy kan ook die distributiewe eienskap gebruik om sommige vermenigvuldiging te vereenvoudig. Jy kan getalle in tiene verdeel met `n res om hoofrekene makliker te maak. Byvoorbeeld, jy kan 8 x 16 herskryf as 8(10+6). Dit is dan bloot 80 + 48 = 128. Nog `n voorbeeld, 7 x 24 = 7(20 + 4) = 7(20) + 7(4) = 140 + 28 = 168. Oefen dit uit die kop en hoofrekene sal baie makliker word.