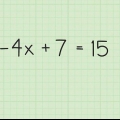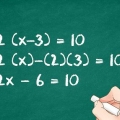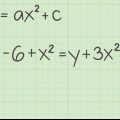4(x+3) + 9 - 5 = 32 
4x + 12 + 9 - 5 = 32 
4x+21-5 = 32 4x+16 = 32 4x + 16 - 16 = 32 - 16 4x = 16 
4x/4 = 16/4 x = 4 
2(x+3)+ 9 - 5 = 32 2(4+3)+ 9 - 5 = 32 2(7) + 9 - 5 = 32 4(7) + 9 - 5 = 32 28 + 9 - 5 = 32 37 - 5 = 32 32 = 32 

2x+12-12 = 44-12 2x = 32 
(2x)/2 = 32/2 x = 16 

2x + 12 = 44 2 x (4) + 12 = 44 2 x 16 + 12 = 44 32 + 12 = 44 44 = 44 

(x + 3)/6 = 2/3 6 x 2 = 12 (x + 3) x 3 = 3x + 9 3x + 9 = 12 
3x + 9 - 9 = 12 - 9 3x = 3 

(x + 3)/6 = 2/3 (1 + 3)/6 = 2/3 4/6 = 2/3 2/3 = 2/3 

√(2x+9) - 5 + 5 = 0 + 5 √(2x+9) = 5 
(√(2x+9)) = 5 2x + 9 = 25 
2x + 9 - 9 = 25 - 9 2x = 16 

√(2x+9) - 5 = 0 √(2(8)+9) - 5 = 0 √(16+9) - 5 = 0 √(25) - 5 = 0 5 - 5 = 0 

|4x +2| - 6 = 8 |4x +2| - 6 + 6 = 8 + 6 |4x +2| = 14 
4x + 2 = 14 4x + 2 - 2 = 14 -2 4x = 12 x = 3 
4x + 2 = -14 4x + 2 - 2 = -14 - 2 4x = -16 4x/4 = -16/4 x = -4 
(Vir x = 3): |4x +2| - 6 = 8 |4(3) +2| - 6 = 8 |12 +2| - 6 = 8 |14| - 6 = 8 14 - 6 = 8 8 = 8 (vir x = -4): |4x +2| - 6 = 8 |4(-4) +2| - 6 = 8 |-16 +2| - 6 = 8 |-14| - 6 = 8 14 - 6 = 8 8 = 8
Los x in 'n vergelyking op
Inhoud
Daar is verskeie maniere om x in `n vergelyking op te los, of jy nou met eksponente en wortels werk of bloot moet deel of vermenigvuldig. Watter metode jy ook al gebruik, jy moet altyd `n manier vind om x van die een kant van die vergelyking te isoleer sodat jy die waarde kan bereken. Hier is hoe om dit te doen:
Trappe
Metode 1 van 5: Gebruik `n gewone lineêre vergelyking

1. Skryf die probleem neer. Hier is die opdrag:
- 2(x+3) + 9 - 5 = 32

2. Werk die eksponent uit. Onthou die volgorde van bewerkings: HMVDOA, wat staan vir Hakies, Eksponensiëring, Deling/Vermenigvuldig, Optel/Aftrek. In hierdie geval kan jy nie eers uitwerk wat tussen hakies is nie, want die x behoort daaraan, so jy begin met die mag, 2. 2 = 4

3. Werk die vermenigvuldiging uit. Vermenigvuldig 4 met (x+3). Hier is hoe:

4. Werk nou die optelling en aftrekking uit. Tel net die oorblywende getalle by of af. Hier is hoe:

5. Isoleer die veranderlike. Jy doen dit deur beide kante van die vergelyking deur 4 te deel om x te vind. 4x/4 = x en 16/4 = 4, dus x = 4.

6. Gaan jou berekening na. Vervang x = 4 terug in die oorspronklike vergelyking om seker te maak dit is korrek. Hier is hoe:
Metode 2 van 5: Met Eksponensiëring

1. Skryf die probleem neer. Kom ons neem aan jy werk aan `n probleem waar die x-term ook `n eksponent bevat:
- 2x + 12 = 44

2. Isoleer die term met die eksponent. Die eerste ding wat jy nou moet doen is om soortgelyke terme te kombineer sodat al die konstantes aan die regterkant van die vergelyking is terwyl die term met die eksponent aan die linkerkant is. Trek net 12 van albei kante af. Hier is hoe:

3. Isoleer die veranderlike met die eksponent deur beide kante te deel deur die koëffisiënt van die x-term. In hierdie geval is 2 die x-koëffisiënt, wat beteken dat beide kante deur 2 gedeel moet word om dit uit te skakel. Hier is hoe:

4. Neem die vierkantswortel van elke kant van die vergelyking. Deur die vierkantswortel van x te bereken, bly jy links met x aan die linkerkant en die vierkantswortel van 16.4, aan die regterkant. Dus, x = 4.

5. Gaan jou berekening na. Vervang x = 4 terug in die oorspronklike vergelyking om seker te maak dit is korrek. Hier is hoe:
Metode 3 van 5: Gebruik Breuke

1. Skryf die probleem neer. Kom ons neem aan dat jy met die volgende probleem te doen het:
- (x + 3)/6 = 2/3

2. Kruis Vermenigvuldig. Om oorkruis te vermenigvuldig, vermenigvuldig die noemer van elke breuk maal die teller van die ander breuk. Dus, vermenigvuldig 6 (die eerste noemer) met 2 (die tweede teller), om 12 aan die regterkant van die vergelyking te kry.Vermenigvuldig dan 3 (die tweede noemer) met x + 3 (die eerste teller), om 3 x + 9 aan die linkerkant van die vergelyking te kry. Hier is hoe dit sal lyk:

3. Kombineer soortgelyke terme. Kombineer die konstantes in die vergelyking deur 9 van beide kante van die vergelyking af te trek. Hier is wat om te doen:

4. Isoleer x deur elke term deur die x-koëffisiënt te deel. Deel net 3x en 9 deur 3, die koëffisiënt van x, en los vir x op. 3x/3 = x en 3/3 = 1, so jy bly met x = 1.

5. Gaan jou berekening na. Om jou werk na te gaan, vervang x terug in die oorspronklike vergelyking om seker te maak dit is korrek. Hier is wat om te doen:
Metode 4 van 5: Gebruik wortelkarakters

1. Skryf die probleem neer. Kom ons neem aan dat jy x in die volgende probleem oplos:
- √(2x+9) - 5 = 0

2. Isoleer die vierkantswortel. Jy moet die vierkantswortelgedeelte van die vergelyking aan die linkerkant van die vergelyking isoleer voordat jy kan voortgaan. So jy tel 5 by aan beide kante van die vergelyking. Hier is hoe:

3. Teken die vierkantswortel van beide kante. Net soos jy albei kante van `n vergelyking deel deur die koëffisiënt vermenigvuldig met x, moet jy ook die vierkantswortel van albei kante van `n vergelyking neem as x onder die radikale teken is. Dit verwyder die radikaal uit die vergelyking. Hier is hoe om dit te doen:

4. Kombineer soortgelyke terme. Kombineer gelyke terme deur 9 van beide kante van die vergelyking af te trek sodat alle konstantes aan die regterkant is, terwyl x aan die linkerkant bly. Hier is wat om te doen:

5. Isoleer die veranderlike. Die laaste ding om te doen om vir x op te los, is om die veranderlike te isoleer deur beide kante van die vergelyking te deel deur 2, die koëffisiënt van die x-term. 2x/2 = x en 16/2 = 8, so jy bly met x = 8.

6. Gaan jou berekening na. Tik weer 8 in die vergelyking vir x om seker te maak dat jou berekening korrek is:
Metode 5 van 5: Gebruik die Absolute Waarde

1. Skryf die probleem neer. Kom ons neem aan jy probeer x oplos in die volgende probleem:
- |4x +2| - 6 = 8

2. Isoleer die absolute waarde. Die eerste ding om te doen is om soortgelyke terme te kombineer en die absolute waarde te isoleer. In hierdie geval kan jy dit doen deur 6 aan beide kante van die vergelyking by te voeg. Hier is hoe:

3. Verwyder die absolute waarde en los die vergelyking op. Dit is die eerste en maklikste stap. Jy moet nou x twee keer oplos, elke keer as jy met `n absolute waarde werk. Hier is hoe om dit die eerste keer te doen:

4. Verwyder die absolute waarde en verander die teken van die terme aan die ander kant van die gelykheidsteken voordat jy voortgaan om op te los. Doen dit nou weer, hierdie keer maak die linkerdeel van die vergelyking gelyk aan -14 in plaas van 14. Hier is hoe:

5. Gaan jou berekening na. Noudat jy weet dat x = (3, -4), vervang net albei getalle terug in die vergelyking om seker te maak dit is reg. Hier is hoe:
Wenke
- Om jou werk na te gaan, voer die waarde van x terug in die oorspronklike vergelyking en los daarvoor op.
- Wortels is `n ander manier om eksponente voor te stel.Die vierkantswortel van x = x^1/2.
Artikels oor die onderwerp "Los x in 'n vergelyking op"
Оцените, пожалуйста статью
Gewilde