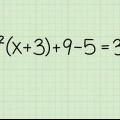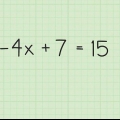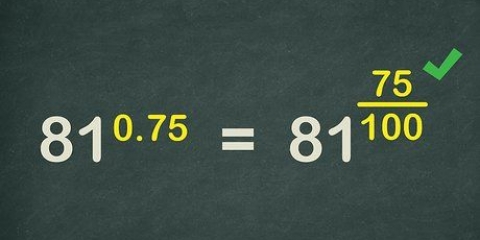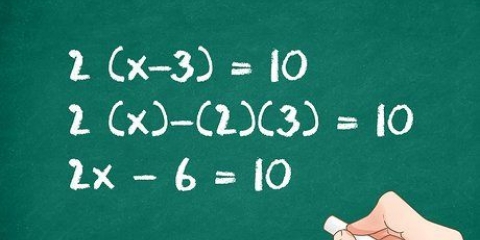Oplos van 'n algebraïese uitdrukking: 10 stappe (met prente)

Inhoud

Trappe
- Deel 1 van 2: Verstaan die basiese beginsels
- Deel 2 van 2: Los `n algebraïese vergelyking op
Wenke

`n Algebraïese uitdrukking is `n wiskundige uitdrukking wat getalle en/of veranderlikes bevat. Alhoewel dit nie opgelos kan word nie omdat dit nie `n gelykheidsteken (=) bevat nie, kan dit vereenvoudig word. Jy kan egter los wiskundige vergelykings op, wat algebraïese uitdrukkings bevat, geskei deur `n gelykheidsteken. As jy hierdie wiskundekonsep wil bemeester, lees verder na stap 1 om te begin.

Trappe

Deel 1 van 2: Verstaan die basiese beginsels

Prent getiteld Los `n algebraïese uitdrukking op Stap 1 op

1. Verstaan die verskil tussen `n algebraïese uitdrukking en `n algebraïese vergelyking. `n Algebraïese uitdrukking is `n wiskundige uitdrukking wat getalle en/of veranderlikes bevat. Dit bevat nie `n gelyke teken nie en kan nie opgelos word nie. `n Algebraïese vergelyking kan egter opgelos word, en behels `n reeks algebraïese uitdrukkings geskei deur `n gelykheidsteken. Hier is `n paar voorbeelde:

Algebraïese uitdrukking: 4x + 2
Algebraïese Vergelyking: 4x + 2 = 100

Prent getiteld Los `n algebraïese uitdrukking op Stap 2 op

2. Leer hoe om soortgelyke terme te kombineer. Om soortgelyke terme te kombineer beteken eenvoudig om die terme van dieselfde graad op te tel (of af te trek). Dit beteken dat alle x terme gekombineer kan word met ander x terme, alle x terme kan gekombineer word met x terme en alle konstantes (getalle wat nie aan veranderlikes gekoppel is nie, soos 8 of 5) kan ook saamgevoeg word, of gekombineer word met mekaar. Hier is `n voorbeeld:

3x + 5 + 4x - x + 2x + 9 =

3x - x + 4x + 2x + 5 + 9 =

2x + 6x + 14

Prent getiteld Los `n algebraïese uitdrukking op Stap 3

3. Leer hoe om `n getal te faktoriseer. As jy met `n algebraïese vergelyking te doen het, wat beteken dat daar `n uitdrukking aan weerskante van `n gelykheidsteken is, kan jy dit vereenvoudig deur die algemene term uit te skakel. Kyk na die koëffisiënte van al die toestande (die getalle voor die veranderlikes, of die konstantes) en kyk of daar `n getal is wat jy kan "wegwerk" deur elke term deur daardie getal te deel. As jy dit kan doen, dan het jy die vergelyking vereenvoudig en jy is op pad om dit op te los. Hier is hoe dit werk:

3x + 15 = 9x + 30

Jy sien dat elke koëffisiënt deelbaar is deur 3. Elimineer die getal 3 deur elke term deur 3 te deel om die vergelyking te vereenvoudig.

3x/3 + 15/3 = 9x/3 + 30/3 =

x + 5 = 3x + 10

Prent getiteld Los `n algebraïese uitdrukking op Stap 4

4. Ken die volgorde van operasies. Die volgorde van bewerkings, ook bekend as die mnemonic `How To Get Rid Of Die Insufficients`, dui die volgorde aan waarin jy die verskillende wiskundige bewerkings moet uitvoer. Die volgorde is: Hakies, Eksponensiëring, Beworteling, Vermenigvuldiging, Deel, Optel en Aftrekking. Hier is `n voorbeeld van hoe die volgorde van bewerkings werk:

(3 + 5) x 10 + 4

Eers die bewerkings tussen hakies:

= (8) x 10 + 4

Dan gaan ons krag verhef:

= 64 x 10 + 4

Dan die vermenigvuldiging:

= 640 + 4

En uiteindelik voeg ons by:

= 644

Prent getiteld Los `n algebraïese uitdrukking op Stap 5

5. Leer om `n veranderlike te isoleer. As jy `n algebraïese vergelyking wil oplos, is jou doel om die veranderlike, dikwels bekend as x, aan die een kant van die vergelyking te kry, en die konstante terme aan die ander kant van die vergelyking. Jy kan x isoleer deur te deel, vermenigvuldig, optel, aftrek, die vierkantswortel te bepaal of ander bewerkings. Sodra jy x geïsoleer het, kan jy dit begin oplos. Hier is hoe om dit te doen:

5x + 15 = 65 =

5x/5 + 15/5 = 65/5 =

x + 3 = 13 =

x = 10

Deel 2 van 2: Los `n algebraïese vergelyking op

Prent getiteld Los `n algebraïese uitdrukking op Stap 6

1. Los `n eenvoudige lineêre algebraïese vergelyking op. `n Lineêre algebraïese vergelyking is mooi en eenvoudig, met slegs die eerstegraadse konstantes en veranderlikes (geen magte of ander kompleksiteit nie). Om dit op te los, al wat jy hoef te doen is om te vermenigvuldig, deel, optel of aftrek wanneer nodig, om die veranderlike te isoleer en op te los vir `x`. Hier is hoe om dit te doen:

4x + 16 = 25 -3x =
4x = 25 -16 - 3x
4x + 3x = 25 -16 =
7x = 9
7x/7 = 9/7 =
x = 9/7

Prent getiteld Los `n algebraïese uitdrukking op Stap 7

2. Los `n algebraïese vergelyking op met magte (eksponente). As die vergelyking magte het, dan hoef jy net `n manier te vind om die krag aan die een kant van die vergelyking te isoleer en dit dan op te los deur die mag te "verwyder" deur die vierkantswortel van beide die mag en dié van die konstant aan die ander kant van die vergelyking. Hier is hoe om dit te doen:

2x + 12 = 44

Trek eers 12 van albei kante af.

2x + 12 -12 = 44 -12 =

2x = 32

Deel nou albei kante deur 2.

2x/2 = 32/2 =

x = 16

Los op deur die vierkantswortel van beide kante te neem, want dit maak x gelyk aan x.

√x = √16 =

Gee albei antwoorde: x = 4, -4

Prent getiteld Los `n algebraïese uitdrukking op Stap 8

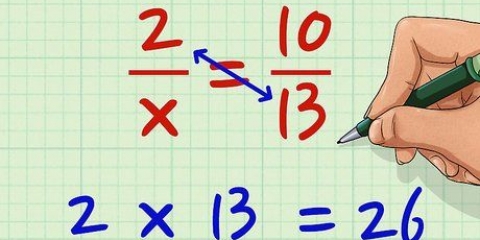
3. Los `n algebraïese uitdrukking op met breuke. Om `n algebraïese uitdrukking op te los wat breuke bevat, moet jy die breuke kruisvermenigvuldig, soortgelyke terme kombineer en dan die veranderlike isoleer. Hier is hoe om dit te doen:

(x + 3)/6 = 2/3

Eerstens gaan jy oorkruis vermenigvuldig om van die breuk ontslae te raak. Vermenigvuldig die teller van een breuk met die noemer van die ander breuk.

(x + 3) x 3 = 2 x 6 =

3x + 9 = 12

Dan kombineer jy gelyke terme. Kombineer die konstante terme 9 en 12 deur 9 van beide kante af te trek.

3x + 9 - 9 = 12 - 9 =

3x = 3

Isoleer die veranderlike, x, deur beide kante deur 3 te deel en jy het die antwoord.

3x/3 = 3/3 =

x = 1

Prent getiteld Los `n algebraïese uitdrukking op Stap 9 op

4. Los `n algebraïese uitdrukking op. As jy te doen het met `n algebraïese uitdrukking met radikale, al wat jy hoef te doen is om `n manier te vind om albei kante te vier sodat jy die radikaal kan uitskakel om vir die veranderlike op te los. Hier is hoe om dit te doen:

√(2x+9) - 5 = 0

Beweeg eers alles wat nie onder die radikaal is nie, na die ander kant van die vergelyking:

√(2x+9) = 5

Vierkant dan albei kante om die radikaal te verwyder:

(√(2x+9)) = 5 =

2x + 9 = 25

Nou kan jy die vergelyking soos gewoonlik oplos deur die konstantes te kombineer en die veranderlike te isoleer:

2x = 25 - 9 =

2x = 16

x = 8

Prent getiteld Los `n algebraïese uitdrukking op Stap 10 op

5. Los `n algebraïese uitdrukking op wat `n absolute waarde bevat. Die absolute waarde van `n getal verteenwoordig sy waarde ongeag of dit positief of negatief is; die absolute waarde is altyd positief. So, byvoorbeeld, is die absolute waarde van -3 (ook bekend as |3|) net 3. Om die absolute waarde te vind, isoleer die absolute waarde en los dan twee keer op vir x (beide vir x waar die absolute waarde eenvoudig verwyder word, en vir x waar die terme aan die ander kant van die gelyke teken van teken verander het, van positief na negatief en omgekeerd). Dit gaan so:

Dit is hoe jy dit uitwerk vir die absolute waarde deur die absolute waarde te isoleer en dit dan te verwyder:

|4x +2| - 6 = 8 =

|4x +2| = 8 + 6 =

|4x +2| = 14 =

4x + 2 = 14 =

4x = 12

x = 3

Los dit nou weer op deur die teken van die term aan die ander kant van die vergelyking om te keer, nadat jy die absolute waarde geïsoleer het:

|4x +2| = 14 =

4x + 2 = -14

4x = -14 -2

4x = -16

4x/4 = -16/4 =

x = -4

Gee nou albei antwoorde: x = -4, 3

Wenke

Om jou antwoord te verdubbel, kan jy na wolfram-alpha gaan.com gaan. Daar kan jy die antwoord kry, wat dikwels in die twee stappe vertoon word.
Sodra jy klaar is, vervang die veranderlike met die antwoord en los dan die som op om te sien of dit korrek is. Indien wel, baie geluk, jy is klaar! Jy het sopas `n algebraïese vergelyking opgelos!
Die graad van `n polinoom is die hoogste mag binne die terme.