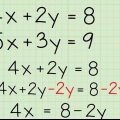2x - 2x = 0 4j - 2j = 2j 8 - 2 = 6 2x + 4y = 8-(2x + 2y = 2)=0 +2y = 6 
2j = 6 Deel 2y en 6 deur 2 en kry y = 3 
Voeg y = 3 in die vergelyking 2x + 2y = 2 in en los op vir x. 2x + 2(3) = 2 2x + 6 = 2 2x = -4 x = - 2 Jy het die stelsel vergelykings deur aftrekking opgelos. (x, y) = (-2, 3) 
Vul (-2, 3) in vir (x, y) in die vergelyking 2x + 4y = 8. 2(-2) + 4(3) = 8 -4 + 12 = 8 8 = 8 Vul (-2, 3) in vir (x, y) in die vergelyking 2x + 2y = 2. 2(-2) + 2(3) = 2 -4 + 6 = 2 2 = 2 

3x + x = 4x 6j + -6j = 0 8 + 4 = 12 As jy dit kombineer, kry jy `n nuwe produk: 3x + 6j = 8 +(x - 6y = 4) = 4x + 0 = 12 
4x + 0 = 12 4x = 12 Deel 4x en 12 deur 3 om x = 3 te kry 
Prop x = 3 in die vergelyking x - 6y = 4 om y te vind. 3 - 6j = 4 -6j = 1 Verdeel -6y en 1 by -6 om y = -1/6 te kry. Jy het die stelsel vergelykings met optelling opgelos. (x, y) = (3, -1/6) 
Vul (3, -1/6) in vir (x, y) in die vergelyking 3x + 6y = 8. 3(3) + 6(-1/6) = 8 9 - 1 = 8 8 = 8 Vul (3, -1/6) in vir (x, y) in die vergelyking x - 6y = 4. 3 - (6 * -1/6) =4 3 - - 1 = 4 3 + 1 = 4 4 = 4 

2 (2x - j = 2) 4x - 2j = 4 
3x + 2j = 10 + 4x - 2j = 4 7x + 0 = 14 7x = 14 

x = 2 ---> 2x - y = 2 4 - j = 2 -y = -2 y = 2 Jy het die stelsel vergelykings deur vermenigvuldiging opgelos. (x, y) = (2, 2) 
Vul (2, 2) in vir (x, y) in die vergelyking 3x + 2y = 10. 3(2) + 2(2) = 10 6 + 4 = 10 10 = 10 Vul (2, 2) in vir (x, y) in die vergelyking 2x - y = 2. 2(2) - 2 = 2 4 - 2 = 2 2 = 2 

x = 2 - 4y --> 2x + 3j = 9 2(2 - 4j) + 3j = 9 4 - 8j + 3j = 9 4 - 5j = 9 -5j = 9 - 4 -5j = 5 -y = 1 y = - 1 
y = -1 --> x = 2 - 4y x = 2 - 4(-1) x = 2 - -4 x = 2 + 4 x = 6 Jy het die stelsel van vergelykings opgelos deur substitusie te gebruik. (x, y) = (6, -1) 
Vul (6, -1) in vir (x, y) in die vergelyking 2x + 3y = 9. 2(6) + 3(-1) = 9 12 - 3 = 9 9 = 9 Vul (6, -1) in vir (x, y) in die vergelyking x + 4y = 2. 6 + 4(-1) = 2 6 - 4 = 2 2 = 2
Oplos van 'n stelsel vergelykings
Inhoud
Om `n stelsel vergelykings op te los, vereis dat die waarde van veelvuldige veranderlikes in veelvuldige vergelykings gevind word. Jy kan `n stelsel vergelykings oplos deur optelling, aftrekking, vermenigvuldiging of substitusie te gebruik. As jy wil leer hoe om `n stelsel van vergelykings op te los, al wat jy hoef te doen is om hierdie stappe te volg.
Trappe
Metode 1 van 4: Los op deur aftrekking

1. Skryf een vergelyking oor die ander. Om hierdie vergelykings met aftrekking op te los is `n ideale metode as jy sien dat beide vergelykings dieselfde veranderlike het met dieselfde koëffisiënt en teken. Byvoorbeeld, as beide vergelykings die veranderlike -2x het, kan jy aftrekking gebruik om die waarde van beide veranderlikes te vind.
- Skryf een vergelyking bo die ander neer sodat die x- en y-veranderlikes van beide vergelykings en die getalle onder mekaar is. Plaas die minusteken langs die onderste nommer.
- Bv.: As jy die volgende twee vergelykings het: 2x + 4y = 8 en 2x + 2y = 2, sal dit so lyk:
- 2x + 4j = 8
- -(2x + 2j = 2)

2. Trek soortgelyke terme af. Noudat die twee vergelykings in lyn is, hoef jy net die soortgelyke terme af te trek. Doen dit met een kwartaal op `n slag:

3. Los op vir die oorblywende kwartaal. Verwyder enige nul uit die vergelyking wat geskep is, dit verander nie die waarde nie, en los die oorblywende vergelyking op.

4. Tik die gevind waarde van die veranderlike in een van die vergelykings. Noudat jy weet dat y = 3, kan jy hierdie waarde in die oorspronklike vergelyking inprop om vir x op te los. Maak nie saak watter vergelyking jy kies nie, die antwoord is dieselfde. Gebruik dus die eenvoudigste vergelyking!

5. Kontroleer jou antwoord. Om seker te maak jou antwoord is korrek, voer albei antwoorde in beide vergelykings in. Hier is hoe om dit te doen:
Metode 2 van 4: Los op deur optel

1. Skryf een vergelyking oor die ander. Om `n stelsel vergelykings deur optelling op te los is die beste metode, as jy agterkom dat beide vergelykings `n veranderlike het met dieselfde koëffisiënt, maar met `n ander teken; byvoorbeeld, as een vergelyking die veranderlike 3x bevat en die ander die veranderlike -3x.
- Skryf een vergelyking bo die ander neer sodat die x- en y-veranderlikes van beide vergelykings en die getalle onder mekaar is. Plaas die plusteken langs die onderste nommer.
- Bv: Jy het die volgende twee vergelykings 3x + 6y = 8 en x - 6y = 4, skryf dan die eerste vergelyking bo die tweede soos hieronder getoon:
- 3x + 6j = 8
- +(x - 6y = 4)

2. Voeg soortgelyke terme saam. Noudat die twee vergelykings bo mekaar in lyn is, hoef jy net die terme met dieselfde veranderlike saam te voeg:

3. Los op vir die oorblywende kwartaal. Verwyder enige nul uit die vergelyking wat ontstaan het, dit verander nie die waarde nie. Los die oorblywende vergelyking op.

4. Tik die gevind waarde van hierdie veranderlike in een van die vergelykings. Noudat jy weet dat x = 3, kan jy hierdie waarde in die oorspronklike vergelyking inprop om vir y op te los. Maak nie saak watter vergelyking jy kies nie, die antwoord is dieselfde. Gebruik dus die eenvoudigste vergelyking!

5. Kontroleer jou antwoord. Om seker te maak jou antwoord is korrek, voer albei antwoorde in beide vergelykings in. Hier is hoe om dit te doen:
Metode 3 van 4: Los op deur vermenigvuldiging

1. Skryf een vergelyking oor die ander. Skryf een vergelyking bo die ander neer sodat die x- en y-veranderlikes van beide vergelykings en die getalle onder mekaar is. As jy vermenigvuldiging gebruik, doen jy dit omdat nie een van die veranderlikes gelyke koëffisiënte het nie - op die oomblik.
- 3x + 2j = 10
- 2x - y = 2

2. Verseker gelyke koëffisiënte. Vermenigvuldig dan een of albei van die vergelykings met `n getal, sodat een van die veranderlikes dieselfde koëffisiënt het. In hierdie geval kan jy die hele tweede vergelyking met 2 vermenigvuldig sodat -y gelyk is aan -2y en dus die eerste y-koëffisiënt. Hier is hoe om dit te doen:

3. Tel of trek die vergelykings af. Al wat jy nou hoef te doen is om gelyke terme uit te skakel deur op te tel of af te trek. Aangesien jy hier met 2y en -2y te doen het, maak dit sin om die optelmetode te gebruik omdat dit gelyk is aan 0. As jy met 2y + 2y te doen het, gebruik die aftrekmetode. Hier is `n voorbeeld van hoe om die optelmetode te gebruik om veranderlikes uit te skakel:

4. Los dit op vir die oorblywende kwartaal. Dit word maklik opgelos deur die waarde van die term te vind wat jy nog nie uitgeskakel het nie. As 7x = 14, dan is x = 2.

5. Tik die gevind waarde in een van die vergelykings. Tik die term in een van die oorspronklike vergelykings om vir die ander term op te los. Kies die eenvoudigste vergelyking hiervoor, dit is die vinnigste.

6. Kontroleer jou antwoord. Om seker te maak jou antwoord is korrek, voer albei antwoorde in beide vergelykings in. Hier is hoe om dit te doen:
Metode 4 van 4: Los op deur vervanging

1. Isoleer `n veranderlike. Vervanging is ideaal wanneer een van die koëffisiënte in een van die vergelykings gelyk is aan 1. Dan is al wat jy hoef te doen is om hierdie veranderlike aan die een kant van die vergelyking te isoleer om die waarde daarvan te vind.
- As jy met die vergelykings 2x + 3y = 9 en x + 4y = 2 werk, dan moet jy x in die tweede vergelyking isoleer.
- x + 4y = 2
- x = 2 - 4y

2. Vul die waarde van die veranderlike wat jy geïsoleer het in die ander vergelyking in. Neem die waarde van die geïsoleerde veranderlike en prop dit in die ander vergelyking. Natuurlik nie in dieselfde vergelyking nie, anders sal jy niks oplos nie. Hier is `n voorbeeld hoe om dit te doen:

3. Los op vir die oorblywende veranderlike. Noudat jy weet dat y = - 1, prop hierdie waarde in die eenvoudiger vergelyking om die waarde van x te vind. Hier is `n voorbeeld van hoe om dit te doen:

4. Kontroleer jou antwoord. Om seker te maak jou antwoord is korrek, voer albei antwoorde in beide vergelykings in. Hier is hoe om dit te doen:
Wenke
- Jy behoort nou enige lineêre stelsel vergelykings te kan oplos deur optel, aftrekking, vermenigvuldiging of substitusie, maar een metode is gewoonlik die geskikste, afhangende van die vergelykings.
Artikels oor die onderwerp "Oplos van 'n stelsel vergelykings"
Оцените, пожалуйста статью
Soortgelyk
Gewilde