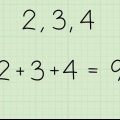Ons gaan voort om met dieselfde voorbeeld te werk,  Kies die tweede en derde nommer van die stel. doen
Kies die tweede en derde nommer van die stel. doen  en jy sal sien dat die verskil steeds gelyk is aan 3. Om dit te bevestig, kies `n ander voorbeeld en doen
en jy sal sien dat die verskil steeds gelyk is aan 3. Om dit te bevestig, kies `n ander voorbeeld en doen  om uit te vind dat die verskil konstant 3 is. Jy kan nou redelik seker wees dat jy met `n rekenkundige ry te doen het.
om uit te vind dat die verskil konstant 3 is. Jy kan nou redelik seker wees dat jy met `n rekenkundige ry te doen het. Dit is moontlik dat `n stel getalle blykbaar die eienskappe van `n rekenkundige ry het wat gebaseer is op die eerste paar getalle, en dan daarvan afwyk. Neem byvoorbeeld die stel  ... Die verskil tussen die eerste en tweede getal is 1 en die verskil tussen die tweede en derde getal is ook 1. Die verskil tussen die derde en vierde getal is egter 3. Aangesien die verskil nie geld vir alle getalle in die hele versameling nie, is dit nie `n rekenkundige ry nie.
... Die verskil tussen die eerste en tweede getal is 1 en die verskil tussen die tweede en derde getal is ook 1. Die verskil tussen die derde en vierde getal is egter 3. Aangesien die verskil nie geld vir alle getalle in die hele versameling nie, is dit nie `n rekenkundige ry nie. 
Byvoorbeeld, in die voorbeeld van  ..., jy kan die volgende getal in die versameling bepaal deur die verskilfaktor 3 by die laaste gegewe getal by te tel. doen
..., jy kan die volgende getal in die versameling bepaal deur die verskilfaktor 3 by die laaste gegewe getal by te tel. doen  en jy kry 16, wat die volgende getal is. Jy kan voortgaan om 3 by te voeg om die volgorde te maak so lank as wat jy wil. Byvoorbeeld, die volgorde kan wees
en jy kry 16, wat die volgende getal is. Jy kan voortgaan om 3 by te voeg om die volgorde te maak so lank as wat jy wil. Byvoorbeeld, die volgorde kan wees ... Jy kan onbepaald hiermee voortgaan.
... Jy kan onbepaald hiermee voortgaan. 

In ons voorbeeld,  ,____,
,____, ..., die onbekende is gelyk aan 4 en die verskil van hierdie reeks is ook 4. Dit word dus opgetel
..., die onbekende is gelyk aan 4 en die verskil van hierdie reeks is ook 4. Dit word dus opgetel  en so kry jy 8, die getal wat ingevul kan word vir die onbekende.
en so kry jy 8, die getal wat ingevul kan word vir die onbekende. 
In die voorbeeld,  ,___,
,___, …, die getal onmiddellik na die onbekende is gelyk aan 12. Trek die verskilfaktor 4 van hierdie getal af en jy kry
…, die getal onmiddellik na die onbekende is gelyk aan 12. Trek die verskilfaktor 4 van hierdie getal af en jy kry  . Die resultaat 8 kan dan ingevul word vir die onbekende.
. Die resultaat 8 kan dan ingevul word vir die onbekende. 
In die voorbeeld, die twee uitkomste van  en
en  albei antwoord 8. Die ontbrekende getal in hierdie rekenkundige ry is dus 8. Die volledige reeks is
albei antwoord 8. Die ontbrekende getal in hierdie rekenkundige ry is dus 8. Die volledige reeks is  ...
... 


Die getal a(n) kan gelees word as "die nde getal van a," waar n die getal in die ry is wat jy wil vind en a(n) die werklike waarde van daardie getal is. Byvoorbeeld, as jy gevra word om die honderdste item van `n rekenkundige ry te vind, is n gelyk aan 100. Let daarop dat n gelyk is aan 100, in hierdie voorbeeld, maar a(n) is die waarde van die honderdste getal, nie die getal 100 self nie. 
Byvoorbeeld, in hierdie voorbeeld,  …, ons weet dat a(1), die eerste getal, gelyk is aan 3 en dat die verskilfaktor d gelyk is aan 5. Gestel jy word gevra om die honderdste getal in daardie ry te vind. Dan n=100 en (n-1)=99. Die volledige eksplisiete formule, met die ingevoerde data, is dan
…, ons weet dat a(1), die eerste getal, gelyk is aan 3 en dat die verskilfaktor d gelyk is aan 5. Gestel jy word gevra om die honderdste getal in daardie ry te vind. Dan n=100 en (n-1)=99. Die volledige eksplisiete formule, met die ingevoerde data, is dan  . Dit kan vereenvoudig word tot 498, die honderdste getal in daardie reeks.
. Dit kan vereenvoudig word tot 498, die honderdste getal in daardie reeks. 

Gebruik die vergelyking  en vul al die inligting in wat jy het. Aangesien jy weet dat die 50ste getal 300 is, weet jy ook dat n=50, n-1=49 en a(n)=300. Daarbenewens word die verskilfaktor d ook gegee, wat 7 is. So word die formule
en vul al die inligting in wat jy het. Aangesien jy weet dat die 50ste getal 300 is, weet jy ook dat n=50, n-1=49 en a(n)=300. Daarbenewens word die verskilfaktor d ook gegee, wat 7 is. So word die formule  . Dit word uitgewerk
. Dit word uitgewerk  . Die reeks wat jy by 43 begin het en het `n verskilfaktor van 7. So die ry lyk soos 43,50,57,64,71,78…293,300.
. Die reeks wat jy by 43 begin het en het `n verskilfaktor van 7. So die ry lyk soos 43,50,57,64,71,78…293,300. 
Gestel jy weet dat `n gegewe rekenkundige ry begin met 100 en optel met 13. Daarbenewens word ook gegee dat die laaste getal 2856 is. Om die lengte van die ry te vind, gebruik die getalle a1=100, d=13 en a(n)=2856. Pas hierdie getalle toe op die formule om te kry  . Sodra jy dit uitgewerk het, sal jy kry
. Sodra jy dit uitgewerk het, sal jy kry  , wat gelyk is aan 212+1, wat weer 213 is. Daar is 213 nommers in daardie ry.
, wat gelyk is aan 212+1, wat weer 213 is. Daar is 213 nommers in daardie ry. Hierdie voorbeeld lyk soos 100, 113, 126, 139 … 2843, 2856.
Bepaling van elke term van 'n rekenkundige ry
Inhoud
`n Rekenkundige ry is enige ry getalle wat opeenvolgend van mekaar verskil deur `n konstante waarde. Byvoorbeeld, die ry van ewe getalle, 
Trappe
Metode 1 van 4: Vind die volgende getal in `n rekenkundige ry

1. Vind die verskilfaktor van die reeks. Wanneer `n versameling getalle aan jou gegee word, kan daar gesê word dat dit `n rekenkundige ry is, of jy sal dit self moet uitvind. Ten minste is die eerste stap dieselfde. Kies die eerste twee opeenvolgende nommers in die stel. Trek die eerste getal van die tweede getal af. Die resultaat is die verskilfaktor van jou reeks.
- Gestel jy het byvoorbeeld die versameling
.... Doen dit dan
om die verskilfaktor 3 te kry.
- Gestel jy het `n versameling dalende getalle, soos
... Dan trek jy steeds die eerste getal van die tweede af om die verskil te vind. In hierdie geval gee dit
. Die negatiewe resultaat beteken dat jou versameling van links na regs afneem. Maak altyd seker dat die teken van die verskil ooreenstem met die rigting waarin die syfers blyk te gaan.

2. Kyk of die verskilfaktor konstant is. Die bepaling van die verskilfaktor vir slegs die eerste twee getalle verseker nie dat die versameling `n rekenkundige ry is nie. Jy moet seker wees dat die verskil konsekwent deur die reeks gehandhaaf word. Kontroleer die verskil deur twee opeenvolgende getalle in die stel af te trek. As die resultaat konsekwent is vir een of twee ander pare getalle, het jy waarskynlik te doen met `n rekenkundige ry.
 Kies die tweede en derde nommer van die stel. doen
Kies die tweede en derde nommer van die stel. doen  en jy sal sien dat die verskil steeds gelyk is aan 3. Om dit te bevestig, kies `n ander voorbeeld en doen
en jy sal sien dat die verskil steeds gelyk is aan 3. Om dit te bevestig, kies `n ander voorbeeld en doen  om uit te vind dat die verskil konstant 3 is. Jy kan nou redelik seker wees dat jy met `n rekenkundige ry te doen het.
om uit te vind dat die verskil konstant 3 is. Jy kan nou redelik seker wees dat jy met `n rekenkundige ry te doen het. ... Die verskil tussen die eerste en tweede getal is 1 en die verskil tussen die tweede en derde getal is ook 1. Die verskil tussen die derde en vierde getal is egter 3. Aangesien die verskil nie geld vir alle getalle in die hele versameling nie, is dit nie `n rekenkundige ry nie.
... Die verskil tussen die eerste en tweede getal is 1 en die verskil tussen die tweede en derde getal is ook 1. Die verskil tussen die derde en vierde getal is egter 3. Aangesien die verskil nie geld vir alle getalle in die hele versameling nie, is dit nie `n rekenkundige ry nie.
3. Tel die verskilfaktor by die laaste getal. Dit is maklik om die volgende getal in `n rekenkundige ry te vind wanneer jy die verskilfaktor ken. Tel net die verskilfaktor by die laaste laaste nommer van die stel en jy kry die volgende nommer.
 ..., jy kan die volgende getal in die versameling bepaal deur die verskilfaktor 3 by die laaste gegewe getal by te tel. doen
..., jy kan die volgende getal in die versameling bepaal deur die verskilfaktor 3 by die laaste gegewe getal by te tel. doen  en jy kry 16, wat die volgende getal is. Jy kan voortgaan om 3 by te voeg om die volgorde te maak so lank as wat jy wil. Byvoorbeeld, die volgorde kan wees
en jy kry 16, wat die volgende getal is. Jy kan voortgaan om 3 by te voeg om die volgorde te maak so lank as wat jy wil. Byvoorbeeld, die volgorde kan wees ... Jy kan onbepaald hiermee voortgaan.
... Jy kan onbepaald hiermee voortgaan.Metode 2 van 4: Soek `n ontbrekende nommer

1. Bevestig dat jy met `n rekenkundige ry begin. In sommige gevalle het jy te doen met `n versameling nommers met `n ontbrekende nommer in die middel. Soos voorheen genoem, begin deur te kontroleer dat jou versameling `n rekenkundige ry is. Kies twee opeenvolgende getalle en vind die verskil tussen hulle. Kontroleer dit dan teen twee ander opeenvolgende getalle in die ry. As die verskil dieselfde is, kan jy aanvaar dat jy met `n rekenkundige ry te doen het, en jy kan voortgaan.
- Gestel jy het byvoorbeeld die volgorde
,___,
... Begin met die aftrekking
en jy kry 4 as verskil. Kontroleer dit teen twee ander opeenvolgende nommers, soos
. Die verskil is weer 4. Jy kan nou voortgaan.

2. Voeg die verskilfaktor by die getal vir die leë spasie. Dit is gelykstaande aan die byvoeging van `n getal aan die einde van `n ry. Soek die nommer direk voor die leë spasie in jou ry. Dit is die `laaste` nommer wat bekend is. Voeg die verskil wat gevind is by hierdie getal, en jy kry die getal wat in die plek van die onbekende moet pas.
 ,____,
,____, ..., die onbekende is gelyk aan 4 en die verskil van hierdie reeks is ook 4. Dit word dus opgetel
..., die onbekende is gelyk aan 4 en die verskil van hierdie reeks is ook 4. Dit word dus opgetel  en so kry jy 8, die getal wat ingevul kan word vir die onbekende.
en so kry jy 8, die getal wat ingevul kan word vir die onbekende.
3. Trek die verskilfaktor van die getal na die onbekende af. Om seker te maak jy het die regte antwoord gekry, kyk weer van die ander rigting af. `n Rekenkundige ry moet konsekwent in `n sekere rigting gaan. As jy van links na regs gaan en aanhou om 4 by te tel, kan jy die teenoorgestelde van regs na links doen en 4 van die vorige getal aftrek.
 ,___,
,___, …, die getal onmiddellik na die onbekende is gelyk aan 12. Trek die verskilfaktor 4 van hierdie getal af en jy kry
…, die getal onmiddellik na die onbekende is gelyk aan 12. Trek die verskilfaktor 4 van hierdie getal af en jy kry  . Die resultaat 8 kan dan ingevul word vir die onbekende.
. Die resultaat 8 kan dan ingevul word vir die onbekende.
4. Vergelyk jou resultate. Die twee uitkomste wat jy kry deur op te tel (van links na regs) of af te trek (van regs na links) moet ooreenstem. Indien wel, dan het jy die ontbrekende nommer gevind. As hulle nie ooreenstem nie, moet jy jou werk weer nagaan. Miskien het jy nie met `n suiwer rekenkundige ry te doen nie.
 en
en  albei antwoord 8. Die ontbrekende getal in hierdie rekenkundige ry is dus 8. Die volledige reeks is
albei antwoord 8. Die ontbrekende getal in hierdie rekenkundige ry is dus 8. Die volledige reeks is  ...
...Metode 3 van 4: Bepaal `n arbitrêre term van `n rekenkundige ry

1. Vind die eerste nommer van die reeks. Nie elke ry begin met die getalle 0 of 1 nie. Kyk na die stel nommers wat jy het en vind die eerste nommer. Dit is jou beginpunt, wat geïdentifiseer kan word met veranderlikes, soos a(1).
- Dit is algemene praktyk vir rekenkundige rye om met die veranderlike a(1) te werk, wat die eerste getal van die ry verteenwoordig. Jy kan natuurlik enige veranderlike kies, maar die uitkoms moet dieselfde wees.
- Byvoorbeeld, gegewe die reeks
…, is die eerste getal
, wat wiskundig aangedui kan word as a(1).

2. Bepaal die verskilfaktor as d. Bepaal die verskilfaktor vir die reeks soos hierbo aangedui. In hierdie voorbeeld is die verskilfaktor gelyk aan  , en dus 5. Wanneer daar teen die ander getalle in die ry gekontroleer word, word dieselfde resultaat verkry. Ons dui hierdie verskilfaktor aan met die wiskundige veranderlike d.
, en dus 5. Wanneer daar teen die ander getalle in die ry gekontroleer word, word dieselfde resultaat verkry. Ons dui hierdie verskilfaktor aan met die wiskundige veranderlike d.
 , en dus 5. Wanneer daar teen die ander getalle in die ry gekontroleer word, word dieselfde resultaat verkry. Ons dui hierdie verskilfaktor aan met die wiskundige veranderlike d.
, en dus 5. Wanneer daar teen die ander getalle in die ry gekontroleer word, word dieselfde resultaat verkry. Ons dui hierdie verskilfaktor aan met die wiskundige veranderlike d.
3. Gebruik die eksplisiete formule. `n Eksplisiete formule is `n wiskundige vergelyking wat jy kan gebruik om enige getal in `n rekenkundige ry te vind sonder om die hele ry uit te skryf. Die eksplisiete formule vir `n wiskundige ry is  .
.
 .
.
4. Vul al die besonderhede in om die probleem op te los. Gebruik hierdie eksplisiete formule vir jou volgorde, vul al die data in wat jy tot jou beskikking het om die getal wat jy benodig te bepaal.
 …, ons weet dat a(1), die eerste getal, gelyk is aan 3 en dat die verskilfaktor d gelyk is aan 5. Gestel jy word gevra om die honderdste getal in daardie ry te vind. Dan n=100 en (n-1)=99. Die volledige eksplisiete formule, met die ingevoerde data, is dan
…, ons weet dat a(1), die eerste getal, gelyk is aan 3 en dat die verskilfaktor d gelyk is aan 5. Gestel jy word gevra om die honderdste getal in daardie ry te vind. Dan n=100 en (n-1)=99. Die volledige eksplisiete formule, met die ingevoerde data, is dan  . Dit kan vereenvoudig word tot 498, die honderdste getal in daardie reeks.
. Dit kan vereenvoudig word tot 498, die honderdste getal in daardie reeks.Metode 4 van 4: Gebruik die eksplisiete formule om meer data te kry

1. Herrangskik die eksplisiete formule om ander veranderlikes te vind. Gebruik die eksplisiete formule en `n paar eenvoudige algebra om verskeie stukke inligting oor die rekenkundige ry te vind. In sy oorspronklike vorm ( ), is die eksplisiete formule wat ontwerp is om an en gee jou die nde nommer van die reeks. Jy kan hierdie formule egter wiskundig manipuleer om ook vir ander veranderlikes op te los.
), is die eksplisiete formule wat ontwerp is om an en gee jou die nde nommer van die reeks. Jy kan hierdie formule egter wiskundig manipuleer om ook vir ander veranderlikes op te los.
 ), is die eksplisiete formule wat ontwerp is om an en gee jou die nde nommer van die reeks. Jy kan hierdie formule egter wiskundig manipuleer om ook vir ander veranderlikes op te los.
), is die eksplisiete formule wat ontwerp is om an en gee jou die nde nommer van die reeks. Jy kan hierdie formule egter wiskundig manipuleer om ook vir ander veranderlikes op te los. - Gestel byvoorbeeld jy ken die einde van `n ry getalle, maar jy wil graag die begin van die ry weet. Herrangskik dan die formule om te kry
- As jy die beginpunt en eindpunt van `n rekenkundige ry ken, maar jy wil weet hoeveel getalle daar in die versameling is, kan jy die eksplisiete formule gebruik om vir n op te los. Dit word dan
.
- As jy eers deur die basiese reëls van algebra wil gaan wat jy nodig het om dit te kan bereken, lees meer oor algebra of eenvoudige algebraïese vergelykings.

2. Vind die eerste nommer van `n reeks. Jy weet dalk dat die 50ste getal in `n rekenkundige ry gelyk is aan 300 en dat die getalle met 7 toeneem (die verskilfaktor), maar jy wil graag weet wat die eerste getal in die ry was. Gebruik die gewysigde eksplisiete formule om a1 op te los om jou antwoord uit te vind.
 en vul al die inligting in wat jy het. Aangesien jy weet dat die 50ste getal 300 is, weet jy ook dat n=50, n-1=49 en a(n)=300. Daarbenewens word die verskilfaktor d ook gegee, wat 7 is. So word die formule
en vul al die inligting in wat jy het. Aangesien jy weet dat die 50ste getal 300 is, weet jy ook dat n=50, n-1=49 en a(n)=300. Daarbenewens word die verskilfaktor d ook gegee, wat 7 is. So word die formule  . Dit word uitgewerk
. Dit word uitgewerk  . Die reeks wat jy by 43 begin het en het `n verskilfaktor van 7. So die ry lyk soos 43,50,57,64,71,78…293,300.
. Die reeks wat jy by 43 begin het en het `n verskilfaktor van 7. So die ry lyk soos 43,50,57,64,71,78…293,300.
3. Bepaal die lengte van `n ry. Gestel jy weet hoe die ry begin en eindig, maar jy moet uitvind hoe lank die ry is. Gebruik dan die gewysigde formule  .
.
 .
. . Sodra jy dit uitgewerk het, sal jy kry
. Sodra jy dit uitgewerk het, sal jy kry  , wat gelyk is aan 212+1, wat weer 213 is. Daar is 213 nommers in daardie ry.
, wat gelyk is aan 212+1, wat weer 213 is. Daar is 213 nommers in daardie ry.Waarskuwings
- Daar is verskillende tipes rye van getalle. Moenie aanneem dat `n stel getalle `n rekenkundige ry is nie. Kontroleer altyd twee pare getalle, verkieslik drie of vier, om die verskilfaktor vir die stel getalle te vind.
Wenke
- Moenie dit vergeet nie d kan óf positief óf negatief wees, afhangende van of dit optel of aftrek is.
Artikels oor die onderwerp "Bepaling van elke term van 'n rekenkundige ry"
Оцените, пожалуйста статью
Soortgelyk
Gewilde