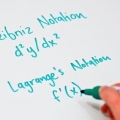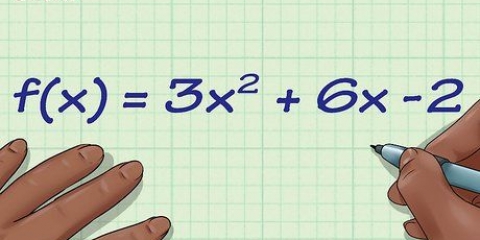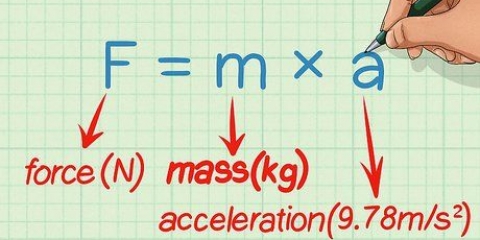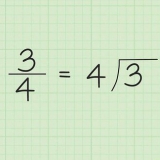Helling = 2 
Helling = -1 
helling = 

Vind die helling van 
Skakel dit om na die vorm  :
: 



Bepaal die helling: Helling = M = 4 

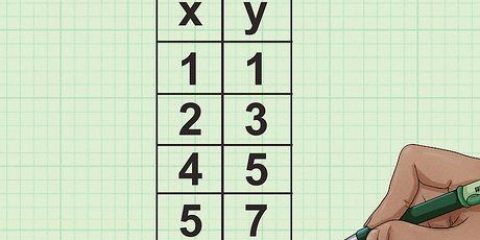
In elke paar is die x-koördinaat die eerste getal, en die y-koördinaat is die tweede getal na die desimale punt. Elke x-koördinaat op `n lyn het `n ooreenstemmende y-koördinaat. 
X1: 2 y1: 4 X2: 6 y2: 6 
Oorspronklike punte: (2.4) en (6.6). Pas op die punt-helling formule toe: 
Vereenvoudig vir die finale antwoord:  = helling
= helling



Met hierdie metode, vra jouself die volgende vraag: "Wat is die helling van die lyn  in punt (4.2)?"
in punt (4.2)?" Die afgeleide word dikwels geskryf as ![Bepaling van die helling van `n lyn f` src=]() of
of 
4 X + 6 

Bepaling van die helling van 'n lyn
Inhoud
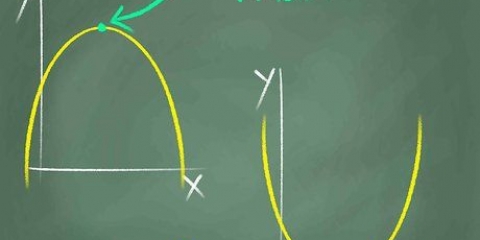
Die helling van `n lyn is `n maatstaf van hoe vinnig die lyn verander. Dit kan met `n reguit lyn gedoen word -- waar die helling jou presies vertel hoe ver op (positiewe helling) of af (negatiewe helling) `n lyn oor `n sekere afstand gaan. Die helling kan ook gebruik word vir `n raaklyn aan `n kromme. Of dit kan `n geboë lyn wees, wat in analise gebruik word, waar die helling ook bekend staan as die `afgeleide` van `n funksie. In elk geval, dink net aan die helling as die "tempo van verandering" van `n grafiek: as die veranderlike "x" groter word, teen watter tempo verander "y"?? Dit is een manier om aan die helling as `n oorsaak en gevolg te dink.
Trappe
Metode 1 van 3: Bepaal die helling van `n lineêre vergelyking

1. Gebruik die helling om te bepaal hoe steil, en in watter rigting (op of af), `n lyn gaan. Om die helling van `n lyn te bepaal is maklik, solank jy `n lineêre vergelyking het of kan opstel. Hierdie metode werk slegs wanneer:
- Die veranderlikes het geen eksponente nie.
- Daar is net twee veranderlikes, en nie een van hulle is breuke nie (die volgende kan byvoorbeeld nie wees nie:
)
- Die vergelyking kan na die vorm vereenvoudig word
, waardeur m en b konstantes (getalle soos 3, 10, -12,
).
2. Vind die getal voor die x, gewoonlik geskryf as `m` om die helling te bepaal. As die vergelyking reeds in die korrekte vorm is,  , kies dan net die getal in die `m` posisie (maar as daar geen getal voor x is nie, is die helling 1). So dit is ook die helling! Weet dat hierdie nommer, m, word altyd vermenigvuldig met die veranderlike, in hierdie geval `n `x`. Kyk na die volgende voorbeelde:
, kies dan net die getal in die `m` posisie (maar as daar geen getal voor x is nie, is die helling 1). So dit is ook die helling! Weet dat hierdie nommer, m, word altyd vermenigvuldig met die veranderlike, in hierdie geval `n `x`. Kyk na die volgende voorbeelde:
 , kies dan net die getal in die `m` posisie (maar as daar geen getal voor x is nie, is die helling 1). So dit is ook die helling! Weet dat hierdie nommer, m, word altyd vermenigvuldig met die veranderlike, in hierdie geval `n `x`. Kyk na die volgende voorbeelde:
, kies dan net die getal in die `m` posisie (maar as daar geen getal voor x is nie, is die helling 1). So dit is ook die helling! Weet dat hierdie nommer, m, word altyd vermenigvuldig met die veranderlike, in hierdie geval `n `x`. Kyk na die volgende voorbeelde:




3. Herken die vergelyking waar een veranderlike geïsoleer is as die helling nie duidelik is nie. Jy kan optel, aftrek, vermenigvuldig, ens. om `n veranderlike te isoleer (gewoonlik die `y`). Onthou dat wat jy ook al aan die een kant van die gelykheidsteken doen (soos om 3 by te voeg), jy dit ook aan die ander kant moet doen. Jou uiteindelike doel is `n vergelyking, soos  . Byvoorbeeld:
. Byvoorbeeld:
 . Byvoorbeeld:
. Byvoorbeeld:
 :
:



Metode 2 van 3: Bepaal die helling met twee punte

1. Gebruik `n grafiek en twee punte om vinnig die helling sonder die vergelyking te vind. As jy `n grafiek en `n lyn het, maar geen vergelyking nie, kan jy steeds die helling met gemak bepaal. Al wat jy nodig het, is twee punte op die lyn, wat jy op die vergelyking toepas  . Wanneer jy die helling bepaal, hou die volgende inligting in gedagte om seker te maak jy is op die regte pad:
. Wanneer jy die helling bepaal, hou die volgende inligting in gedagte om seker te maak jy is op die regte pad:
 . Wanneer jy die helling bepaal, hou die volgende inligting in gedagte om seker te maak jy is op die regte pad:
. Wanneer jy die helling bepaal, hou die volgende inligting in gedagte om seker te maak jy is op die regte pad: - Positiewe hellings gaan op en na regs.
- Negatiewe hellings gaan af en na regs.
- Steiler hellings is steiler lyne. Minder steil hellings is altyd meer geleidelik.
- Perfekte horisontale lyne het `n helling van nul.
- Perfek vertikale lyne het geen helling nie. Hul helling (of helling) is `ongedefinieerd`.

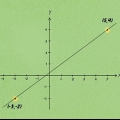
2. Kies twee punte en plaas hulle in die eenvoudige (x, y) vorm. Gebruik die grafiek (of opdragvraag) om die x- en y-koördinate van twee punte op die grafiek te vind. Hulle kan bestaan uit enige twee punte waardeur die lyn gaan. Veronderstel byvoorbeeld dat in hierdie metode die lyn deur die punt (2.4) en deur (6.6) gaan.

3. Benoem die punte x1, y1, X2, y2, en hou elke punt met sy paar. Gaan voort met ons eerste voorbeeld, gebruik die punte (2.4) en (6.6), benoem die x- en y-koördinate van elke punt. As alles goed gegaan het, eindig jy nou met:

4. Vervang hierdie punte in die `punthellingsformule` om die helling te vind. Die volgende formule word gebruik om die helling te bepaal deur enige twee punte op `n reguit lyn te gebruik:  . Vervang net die vier punte en vereenvoudig:
. Vervang net die vier punte en vereenvoudig:
 . Vervang net die vier punte en vereenvoudig:
. Vervang net die vier punte en vereenvoudig:
 = helling
= helling
5. Verstaan hoe die punthellingsformule werk. Die helling van `n lyn word aangedui deur die verandering van y vanaf x (y/x): hoeveel die lyn opgaan gedeel deur hoeveel die lyn na regs voortduur. Die toename van die lyn is die verskil tussen die y-waardes (onthou, die y-as gaan op en af), en die toename van die lyn is die verskil tussen die x-waardes (en die x-as gaan van links na regs).

6. Leer ander maniere wat jy moet weet om die helling te bepaal. Die vergelyking van die helling is  . Dit kan ook voorgestel word deur die Griekse letter `Δ` (`delta`), wat `verskil` beteken. Helling kan ook voorgestel word as Δy/Δx, wat beteken `verskil van y` / `verskil van x`. Dit is presies dieselfde vraag as "Bepaal die helling tussen.."
. Dit kan ook voorgestel word deur die Griekse letter `Δ` (`delta`), wat `verskil` beteken. Helling kan ook voorgestel word as Δy/Δx, wat beteken `verskil van y` / `verskil van x`. Dit is presies dieselfde vraag as "Bepaal die helling tussen.."
 . Dit kan ook voorgestel word deur die Griekse letter `Δ` (`delta`), wat `verskil` beteken. Helling kan ook voorgestel word as Δy/Δx, wat beteken `verskil van y` / `verskil van x`. Dit is presies dieselfde vraag as "Bepaal die helling tussen.."
. Dit kan ook voorgestel word deur die Griekse letter `Δ` (`delta`), wat `verskil` beteken. Helling kan ook voorgestel word as Δy/Δx, wat beteken `verskil van y` / `verskil van x`. Dit is presies dieselfde vraag as "Bepaal die helling tussen.."Metode 3 van 3: Gebruik differensiaalrekening om die helling van `n kromme te vind

1. Hersien hoe jy die afgeleide van algemene funksies op verskillende maniere kan bepaal. Afgeleides gee jou die tempo van verandering (of helling) op een punt op `n lyn. Die lyn kan geboë of reguit wees – dit maak nie saak nie. Onthou hoe die lyn op enige gegewe tydstip verander, eerder as hoe die helling van die hele lyn verander. Hoe jy die afgeleide bepaal hang af van die tipe funksie, so hersien hoe om die afgeleide van funksies te bepaal voordat jy voortgaan.
- Lees hier oor die bepaling van die afgeleide
- Die eenvoudigste afgeleides, dié vir standaard eksponensiële vergelykings, jy kan maklik vind met `n vinnige metode. Jy sal dit in die res van die metode gebruik.

2. Verstaan watter probleme vereis dat jy die helling met afgeleides moet bereken. Jy sal nie altyd eksplisiet gevra word vir die afgeleide of helling van `n kromme nie. Jy kan ook gevra word oor die `tempo van verandering` by punt (x, y). Jy kan gevra word vir `n vergelyking vir die helling van die grafiek, wat eenvoudig beteken om die afgeleide te vind. Ten slotte, kan jy gevra word vir `die helling van die raaklyn in (x, y)`. Dit beteken weer dat dit slegs vra vir die helling van die kromme by `n spesifieke punt (x, y).
 in punt (4.2)?"
in punt (4.2)?"
3.Vind die afgeleide van die funksie. Jy het nie eers `n regte grafiek nodig nie, net die funksie of vergelyking van die grafiek. In hierdie voorbeeld gebruik ons `n voorheen bespreekte funksie,


4.Vervang die punt in die vergelyking van die afgeleide om die helling te vind. Die differensiaal van `n funksie gee jou die helling van die funksie by `n gegewe punt. Met ander woorde, f"(x) is die helling van die funksie te eniger tyd (x,f(x)). So vir hierdie oefenprobleem:
Artikels oor die onderwerp "Bepaling van die helling van 'n lyn"
Оцените, пожалуйста статью
Soortgelyk
Gewilde