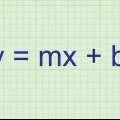Die korrelasiekoëffisiënt, aangedui as r of ρ, is die maatstaf van die lineêre korrelasie (die verhouding, beide in sterkte en rigting) tussen twee veranderlikes. Dit wissel van -1 tot +1, met behulp van plus- en minustekens om die positiewe en negatiewe korrelasie voor te stel. As die korrelasiekoëffisiënt presies -1 is, dan is die verband tussen die twee veranderlikes heeltemal negatief; as die korrelasiekoëffisiënt presies +1 is, dan is die verband heeltemal positief. Twee veranderlikes kan `n positiewe korrelasie, `n negatiewe korrelasie of geen korrelasie hê nie. Jy kan die korrelasie met die hand bereken, met behulp van `n paar gratis korrelasie sakrekenaars wat aanlyn beskikbaar is, of deur die statistiese funksies van `n goeie grafiese sakrekenaar te gebruik.
Trappe
Metode 1 van 4: Berekening van die korrelasiekoëffisiënt met die hand
1.
Versamel eers jou data. Om `n doeltreffende korrelasie te begin bereken, ondersoek eers die datapare. Dit is nuttig om hulle in `n tabel te plaas, beide vertikaal en horisontaal. Benoem elke ry of kolom x en y.
- Byvoorbeeld: veronderstel jy het vier datapare vir X en y. Die tabel kan dan so lyk:
- x || y
- 1 || 1
- 2 || 3
- 4 || 5
- 5 || 7
2. Bereken die gemiddelde van X. Om die gemiddelde te bereken, moet jy al die waardes van byvoeg X tel op en deel dan deur die aantal waardes.
Begin van die bogenoemde voorbeeld, let op dat jy vier waardes het vir X. Om die gemiddelde te bereken, tel alle waardes vir X en deel dit deur 4. Die berekening lyk dan so:


3. Vind die gemiddelde van y. Om die gemiddelde van te kry y Om dit te vind, volg dieselfde stappe, voeg al die waardes van y bymekaar en deel dan deur die aantal waardes.
In die voorbeeld hierbo het jy ook vier waardes vir y. Tel al hierdie waardes bymekaar en deel dan deur 4. Die berekeninge sal dan soos volg lyk:


4. Bepaal die standaardafwyking van X. Sodra jy jou middele het, kan jy die standaardafwyking bereken. Gebruik die formule hiervoor:
 Met die voorbeelddata sal jou berekeninge soos volg lyk:
Met die voorbeelddata sal jou berekeninge soos volg lyk:




5. Bereken die standaardafwyking van y. Deur dieselfde basiese stappe te gebruik, vind die standaardafwyking van y. Jy gaan dieselfde formule gebruik deur die datapunte vir y te gebruik.
Met die voorbeelddata sal jou berekeninge soos volg lyk:




6. Kyk na die basiese formule vir die bepaling van `n korrelasiekoëffisiënt. Die formule vir die berekening van `n korrelasiekoëffisiënt gebruik gemiddeldes, standaardafwykings en die aantal pare in `n datastel (verteenwoordig deur n). Die korrelasiekoëffisiënt self word voorgestel deur die kleinletter r of die Griekse letter ρ (rho). Vir hierdie artikel gebruik ons die formule bekend as die Pearson-korrelasiekoëffisiënt soos hieronder getoon:
 Jy mag dalk effense variasies in die formule, hier of in ander verduidelikings opmerk. Sommige sal byvoorbeeld die Griekse notasie met rho en sigma gebruik, terwyl ander r en s sal gebruik. Sommige verduidelikings kan effens verskillende formules gebruik, maar hulle sal wiskundig gelykstaande wees aan hierdie een.
Jy mag dalk effense variasies in die formule, hier of in ander verduidelikings opmerk. Sommige sal byvoorbeeld die Griekse notasie met rho en sigma gebruik, terwyl ander r en s sal gebruik. Sommige verduidelikings kan effens verskillende formules gebruik, maar hulle sal wiskundig gelykstaande wees aan hierdie een.7. Bepaal die korrelasiekoëffisiënt. Jy het nou die gemiddeldes en standaardafwykings vir jou veranderlikes, sodat jy kan aanbeweeg na die korrelasiekoëffisiëntformule. Onthou dat n verteenwoordig die aantal waardes wat jy het. Jy het reeds die ander relevante inligting in die stappe hierbo uitgewerk.
Deur die voorbeelddata te gebruik, kan jy die data in die korrelasiekoëffisiëntformule invoer en dit so bereken:
 [
[
 ]
]



8. Interpreteer die resultaat. Vir hierdie datastel is die korrelasiekoëffisiënt 0,988. Hierdie nommer vertel jou twee dinge oor die data. Kyk na die teken van die getal en die grootte van die getal.
Aangesien die korrelasiekoëffisiënt positief is, kan jy sê dat daar `n positiewe korrelasie tussen die x-data en die y-data is. Dit beteken dat namate die x-waardes toeneem, verwag jy dat die y-waardes ook sal toeneem.Aangesien die korrelasiekoëffisiënt baie naby aan +1 is, is die x-data en y-data baie nou verwant. As jy hierdie punte sou teken, sou jy sien dat hulle `n baie goeie benadering van `n reguit lyn is.Metode 2 van 4: Gebruik aanlyn korrelasie sakrekenaars
1. Soek aanlyn vir korrelasie sakrekenaars. Die meting van korrelasie is `n redelik standaardberekening vir statistici. Die berekening kan baie vervelig raak vir groot datastelle as dit met die hand gedoen word. Daarom het baie bronne algemene korrelasieberekeninge aanlyn beskikbaar gestel. Gebruik enige soekenjin en voer die soekterm `korrelasie sakrekenaar` in.
2. Vir die data in. Lees asseblief die instruksies op die webwerf aandagtig deur sodat jy die data korrek kan invoer. Dit is belangrik dat datapare in orde gehou word of jy sal `n verkeerde korrelasieresultaat kry. Verskillende webwerwe gebruik verskillende formatering om data in te voer.
Byvoorbeeld: op die webwerf http://nrekenaars.com/statistieke/korrelasie-koëffisiënt-sakrekenaar.htm vind `n horisontale blokkie om x-waardes in te voer en `n tweede horisontale blokkie om y-waardes in te voer. Jy voer die terme in wat slegs deur kommas geskei word. Die x-datastel wat vroeër in hierdie artikel bereken is, moet dus ingevoer word as 1,2,4,5. Die y-datastel word ingevoer as 1,3,5,7.Op `n ander webwerf, http://www.alkohol.com/sakrekenaars/statistieke/korrelasiekoëffisiënt/, jy kan data horisontaal en vertikaal invoer, solank jy die datapunte in orde hou.3. Bereken die resultate. Hierdie berekeningwebwerwe is gewild, want oor die algemeen, nadat u die data ingevoer het, hoef u net op die `Bereken`-knoppie te klik -- die resultaat sal outomaties verskyn.
Metode 3 van 4: Gebruik `n grafiese sakrekenaar
1.
Voer jou besonderhede in. Skakel die statistiekfunksie op jou grafiese sakrekenaar aan en kies dan die opdrag `Redigeer`.
- Elke sakrekenaar het effens verskillende sleutelopdragte. Hierdie artikel verskaf spesifieke instruksies vir die Texas Instruments TI-86.
- Voer die Stat-funksie in deur [2nd]-Stat (bo die `+`-sleutel) te druk en dan F2-Edit.
2. Vee alle ou gestoorde data uit. Die meeste sakrekenaars sal die statistiese data hou totdat dit uitgevee is. Om seker te maak dat jy nie ou data met nuwe data verwar nie, moet jy eers alle voorheen gestoor inligting uitvee.
Gebruik die pyltjie sleutels om die wyser te beweeg om die kategorie `xStat` te merk. Druk dan `Clear` en `Enter`. Dit behoort alle waardes in die xStat-kolom uit te vee.Gebruik die pyltjie sleutels om die `yStat`-kategorie uit te lig. Druk `Clear` en `Enter` om die data uit daardie kolom ook skoon te maak.3. Voer jou datawaardes in. Gebruik die pyltjie sleutels om die wyser na die eerste spasie onder die xStat-opskrif te skuif. Tik jou eerste datawaarde in en druk dan Enter. Jy behoort die spasie onderaan die skerm `xStat(1)=__` te sien waar jou waarde die leë spasie vul. Wanneer jy Enter druk, sal die data die tabel vul, die wyser sal na die volgende reël beweeg, en die reël onderaan die skerm behoort nou `xStat(2)=__` te lees.
Gaan voort om alle x-waardes in te voer.Sodra jy die x-waardes ingevoer het, gebruik die pyltjiesleutels om na die yStat-kolom te beweeg en voer die y-waardes in.Wanneer alle data ingevoer is, druk Exit om die skerm skoon te maak en die Stat-kieslys te verlaat.4. Bereken die lineêre regressiestatistiek. Die korrelasiekoëffisiënt is `n maatstaf van hoe goed die data `n reguit lyn benader. `n Grafiese sakrekenaar met statistiese funksies kan baie vinnig die beste paslyn en korrelasiekoëffisiënt bereken.
Voer die Stat-funksie in en druk dan die Calc-knoppie. Op die TI-86 is dit [2de][Stat][F1].Kies die lineêre regressieberekeninge. Op die TI-86 is dit [F3], gemerk "LinR.` Die grafiese skerm sal dan die reël `LinR _` met `n flikkerende wyser wys.Jy moet nou die name van die twee veranderlikes wat jy wil bereken intik. Dit is xStat en yStat.Op die TI-86, kies die lys name (`Name`) deur [2nd][List][F3] te druk.Die onderste lyn van jou skerm behoort nou die beskikbare veranderlikes te wys. Kies [xStat] (dit is waarskynlik knoppie F1 of F2), voer dan `n komma in en dan [yStat].Druk Enter om die data te bereken5. Interpreteer die resultate. Wanneer jy Enter druk, sal die sakrekenaar onmiddellik die volgende inligting bereken vir die data wat jy ingevoer het:
 : Dit is die algemene formule vir `n reguit lyn. In plaas van die bekende `y=mx+b` word dit egter in omgekeerde volgorde aangebied.
: Dit is die algemene formule vir `n reguit lyn. In plaas van die bekende `y=mx+b` word dit egter in omgekeerde volgorde aangebied. . Dit is die waarde van die kruising met die y-as van die lyn wat die beste pas.
. Dit is die waarde van die kruising met die y-as van die lyn wat die beste pas. . Dit is die helling van die lyn wat die beste pas.
. Dit is die helling van die lyn wat die beste pas. . Dit is die korrelasiekoëffisiënt.
. Dit is die korrelasiekoëffisiënt. . Dit is die aantal datapare wat in die berekening gebruik word.
. Dit is die aantal datapare wat in die berekening gebruik word.Metode 4 van 4: Herhaal die basiese beginsels
1.
Verstaan die konsep van korrelasie. Korrelasie verwys na die statistiese verband tussen twee hoeveelhede. Die korrelasiekoëffisiënt is `n enkele getal wat jy vir twee stelle datapunte kan bereken. Die getal is altyd iets tussen -1 en +1, en dui aan hoe nou die twee datastelle verbind is.
- Byvoorbeeld, as jy die lengte en ouderdom van kinders tot ongeveer 12 jaar oud gemeet het, sou jy verwag om `n sterk positiewe korrelasie te vind. Soos kinders ouer word, is hulle geneig om langer te word.
- `n Voorbeeld van `n negatiewe korrelasie is die vergelyking van die tyd wat iemand spandeer om gholf te oefen en daardie persoon se gholftelling. Soos die oefening vorder, behoort die telling te daal.
- Uiteindelik sou u min korrelasie, positief of negatief, tussen byvoorbeeld `n persoon se skoengrootte en hul eksamenpunte verwag.

2. Bereken die gemiddelde. Die rekenkundige gemiddelde, of "gemiddelde," van `n stel data word bereken deur al die waardes van die data bymekaar te tel en dan te deel deur die aantal waardes in die stel. Wanneer jy die korrelasiekoëffisiënt vir jou data wil bepaal, moet jy die gemiddelde van elke stel data bereken.
Die gemiddelde van `n veranderlike word aangedui deur die veranderlike met `n horisontale lyn bo dit. Dit word dikwels na verwys as `x-bar` of `y-bar` vir die datastelle van x en y. Alternatiewelik kan die gemiddelde aangedui word deur die kleinletter Griekse letter μ (mu). Byvoorbeeld, om die gemiddelde van datapunte van x voor te stel, kan jy μ gebruikX of μ(x).Byvoorbeeld, as jy `n stel van x (1,2,5,6,9,10) het, dan sal die gemiddelde van hierdie data soos volg bereken word:


3. Ken die belangrikheid van die standaardafwyking. In statistiek meet die standaardafwyking variasie, wat die verspreiding van die getalle relatief tot die gemiddelde toon. `n Groep getalle met `n lae standaardafwyking is redelik naby aan mekaar. `n Groep getalle met `n hoë standaardafwyking is meer verspreid.
As `n simbool word die standaardafwyking uitgedruk met die kleinletter s of die Griekse letter σ (sigma). Dus word die standaardafwyking van die x-data geskryf as sX ofX.4. Herken die opsommingsnotasie. Die opteloperateur is een van die mees algemene operateurs in wiskunde, wat `n som van waardes verteenwoordig. Dit word voorgestel deur die Griekse hoofletter, sigma of ∑.
Byvoorbeeld, as jy `n stel datapunte x (1,2,5,6,9,10) het, dan beteken ∑x:1+2+5+6+9+10 = 33Wenke
- Daar word soms na die korrelasiekoëffisiënt verwys as die `Pearson produk-oomblikkorrelasiekoëffisiënt`, ter ere van Karl Pearson, sy ontwikkelaar.
- Oor die algemeen verteenwoordig `n korrelasiekoëffisiënt groter as 0.8 (positief of negatief) `n sterk korrelasie; `n korrelasiekoëffisiënt laer as 0.5 (weereens positief of negatief) verteenwoordig `n swak korrelasiekoëffisiënt.
Waarskuwings
- Korrelasie toon dat twee stelle data op een of ander manier verbind is. Wees egter versigtig om dit nie as `n oorsaaklike verband te interpreteer nie. Byvoorbeeld, as jy mense se skoengroottes en hul lengte vergelyk, sal jy waarskynlik `n sterk positiewe korrelasie vind. Groter mense het oor die algemeen groter voete. Dit beteken egter nie dat om lank te word jou voete sal laat groei, of dat groot voete jou lank sal maak nie. Hulle gebeur sommer saam.
Artikels oor die onderwerp "Bepaling van die korrelasiekoëffisiënt"


























 [
[
 ]
]












 : Dit is die algemene formule vir `n reguit lyn. In plaas van die bekende `y=mx+b` word dit egter in omgekeerde volgorde aangebied.
: Dit is die algemene formule vir `n reguit lyn. In plaas van die bekende `y=mx+b` word dit egter in omgekeerde volgorde aangebied. . Dit is die waarde van die kruising met die y-as van die lyn wat die beste pas.
. Dit is die waarde van die kruising met die y-as van die lyn wat die beste pas. . Dit is die helling van die lyn wat die beste pas.
. Dit is die helling van die lyn wat die beste pas. . Dit is die korrelasiekoëffisiënt.
. Dit is die korrelasiekoëffisiënt. . Dit is die aantal datapare wat in die berekening gebruik word.
. Dit is die aantal datapare wat in die berekening gebruik word.