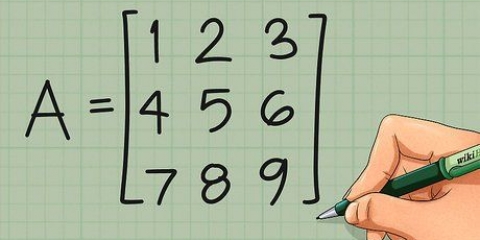Kom ons kies die eerste ry van ons voorbeeldmatriks A. Omkring die 1 5 3. In algemene terme, omkring a11 a12 a13. 
In ons voorbeeld is die verwysingsry 1 5 3. Dit eerste element is in ry 1 en kolom 1. Trek ry 1 en kolom 1 heeltemal deur. Skryf die oorblywende elemente neer as a2 x 2 matriks: 1 5 3
2 4 7
4 6 2
In ons voorbeeld is die determinant van die matriks  = 4 * 2 - 7 * 6 = -34.
= 4 * 2 - 7 * 6 = -34. Hierdie determinant word die minderjarige van die element wat ons in ons oorspronklike matriks gekies het. In hierdie geval het ons die minderjarige van a11 het dit gekry. 
In ons voorbeeld het ons `n11 gekies, wat `n waarde van 1 het. Vermenigvuldig dit met -34 (die determinant van die 2x2 matriks) om 1*-34 = -34 om te kry. 
+ - +
- + -
+ - + Omdat ons a11 gekies het, gemerk met `n +, ons vermenigvuldig die getal met +1 (met ander woorde, ons doen niks daarmee nie). Die antwoord is steeds -34. Nog `n manier om die teken te bepaal, is met die formule (-1), waar i en j vorm die ry en kolom van die element. 
Kruis die ry en kolom van daardie element. In hierdie geval kies jy die element a12 (met waarde 5). Kruis die eerste ry (1 5 3) en die tweede kolom  .
. Behandel die oorblywende elemente as `n 2x2 matriks. In ons voorbeeld is die matriks 
Bepaal die determinant van hierdie 2x2 matriks. Gebruik die formule ad - bc. (2*2 - 7*4 = -24) Vermenigvuldig dit met die gekose element van die 3x3-matriks. -24 * 5 = -120 Bepaal of jy met -1 moet vermenigvuldig. Gebruik die karaktertabel of die formule (-1). Ons het element a12 gekies, en dit is `n – op die karaktertabel. Ons moet die teken van ons antwoord verander: (-1)*(-120) = 120. 
Kruis ry 1 en kolom 3 en kry 
Die determinant daarvan is 2*6 - 4*4 = -4. Vermenigvuldig dit met die element a13: -4 * 3 = -12. element a13 is `n + op die karaktertabel, so die antwoord is -12. 
In ons voorbeeld is die determinant -34 + 120 + -12 = 74. 

Gestel jy het byvoorbeeld `n 3x3 matriks: 
Elke 9 in posisie a11 om daarvan ontslae te raak, kan ons die tweede ry met -3 vermenigvuldig en die resultaat by die eerste een tel. Die nuwe eerste ry word dan [9 -1 2] + [-9 -3 0] = [0 -4 2]. Die nuwe matriks is  Probeer om dieselfde truuk vir die kolomme te gebruik, om12 om `n 0 te maak.
Probeer om dieselfde truuk vir die kolomme te gebruik, om12 om `n 0 te maak. 
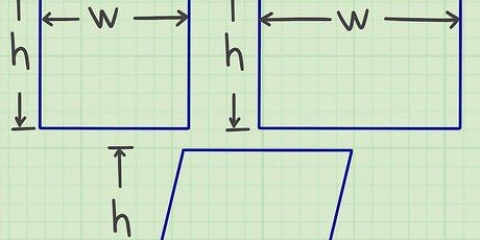
Boonste driehoekmatriks: Alle nie-nul elemente is op of bo die hoofhoeklyn. Alle waardes hieronder is nul. Onderste driehoekmatriks: Alle nie-nul elemente is op of onder die hoof diagonaal. Diagonale matriks: Alle nie-nul elemente is op die hoof diagonaal. (`n Subset van bogenoemde.)
Bepaling van die determinant van 'n 3x3 matriks
Inhoud
Die determinant van `n matriks word wyd gebruik in wiskunde, lineêre algebra en hoër meetkunde. Buite die wetenskaplike wêreld gebruik rekenaargrafiese ingenieurs en programmeerders gereeld die determinante van matrikse. Lees hierdie artikel om die determinant van `n 3x3-matriks te bepaal.
Trappe
Deel 1 van 2: Bepaling van die determinant

1. Skryf jou 3 x 3 matriks neer. Ons begin met `n 3 x 3 matriks A en probeer die determinant |A| om daarvan te hou. Ons gebruik die volgende algemene notasie vir die matriks (en dit is ons voorbeeldmatriks):

2. Kies een ry of kolom. Dit sal jou verwysingsry of kolom wees. Jy sal dieselfde antwoord kry, maak nie saak watter een jy kies nie. Kies nou net die eerste ry. Ons sal jou later raad gee oor hoe om die opsie te kies wat die maklikste is om te bereken.

3. Trek die ry en kolom van die eerste element deur. Kyk na die ry of kolom wat jy omkring en kies die eerste element. Trek `n lyn deur die ooreenstemmende ry en kolom. As alles goed gaan, lewer dit nou vier syfers op. Ons hanteer dit as `n 2 x 2 matriks.

4. Bepaal die determinant van die 2 x 2 matriks. Moenie vergeet nie: die matriks  het `n determinant van advertensie - bc. Jy weet dit deur `n kruis (X) deur die 2 x 2 matriks te trek. Vermenigvuldig die twee getalle wat met die van die X verbind word. Trek dan die produk af van die twee getalle wat deur die / verbind word. Gebruik hierdie formule om die determinant van die matriks wat jy sopas gevind het, te bereken.
het `n determinant van advertensie - bc. Jy weet dit deur `n kruis (X) deur die 2 x 2 matriks te trek. Vermenigvuldig die twee getalle wat met die van die X verbind word. Trek dan die produk af van die twee getalle wat deur die / verbind word. Gebruik hierdie formule om die determinant van die matriks wat jy sopas gevind het, te bereken.
 het `n determinant van advertensie - bc. Jy weet dit deur `n kruis (X) deur die 2 x 2 matriks te trek. Vermenigvuldig die twee getalle wat met die van die X verbind word. Trek dan die produk af van die twee getalle wat deur die / verbind word. Gebruik hierdie formule om die determinant van die matriks wat jy sopas gevind het, te bereken.
het `n determinant van advertensie - bc. Jy weet dit deur `n kruis (X) deur die 2 x 2 matriks te trek. Vermenigvuldig die twee getalle wat met die van die X verbind word. Trek dan die produk af van die twee getalle wat deur die / verbind word. Gebruik hierdie formule om die determinant van die matriks wat jy sopas gevind het, te bereken. = 4 * 2 - 7 * 6 = -34.
= 4 * 2 - 7 * 6 = -34.
5. Vermenigvuldig die antwoord met jou gekose element. Onthou dat jy `n element uit jou verwysingsry (of kolom) gekies het toe jy besluit het watter ry en kolom om deur te trek. Vermenigvuldig hierdie element met die determinant wat jy pas vir die 2x2-matriks bereken het.

6. Bepaal die teken van jou antwoord. Vermenigvuldig nou die antwoord met 1 of met -1 om die kofaktor van jou gekose element. Watter een jy gebruik hang af van die posisie van die element in die 3x3-matriks. Memoriseer die volgende eenvoudige tabel om uit te vind watter element wat veroorsaak:
- + -
+ - +

7. Herhaal hierdie proses vir die tweede element in jou verwysingsry of -kolom. Gaan voort met die oorspronklike 3x3-matriks, met die ry of kolom wat jy vroeër omsirkel het. Herhaal dieselfde proses met hierdie element:
 .
.

8. Herhaal vir die derde element. Jy moet nou `n kofaktor vind. Bereken i vir die derde term in jou verwysingsry of -kolom. Hier is `n vinnige verduideliking van hoe om die kofaktor van te bereken 13 in ons voorbeeld:


9. Voeg die drie resultate bymekaar. Dit is die laaste stap. Jy het kofaktore bereken, een vir elke element in `n enkele ry of kolom. Voeg dit bymekaar en jy het die determinant van die 3x3-matriks gevind.
Deel 2 van 2: Vereenvoudig die probleem

1. Kies die verwysing met die meeste nulle. Moenie vergeet dat jy elk kan ry of kolom as verwysing kies. Jy sal dieselfde antwoord kry, maak nie saak wat jy kies nie. As jy `n ry of kolom met nulle kies, hoef jy net die kofaktor te bereken van die elemente wat nie nul is nie. Die rede is soos volg:
- Gestel jy kies ry 2, met die elemente a21, a22, en a23. Om hierdie probleem op te los kyk ons na drie verskillende 2x2-matrikse. Gestel ons noem dit A21, a22 en A23.
- Die determinant van die 3x3-matriks is a21|A21| - a22|A22| + a23|A23|.
- Indien die bepalings a22 en a23 is albei 0, dan word ons formule21|A21| - 0*|A22| + 0*|A23| = a21|A21| - 0 + 0 = a21|A21|. Nou moet ons net die kofaktor van `n enkele element bereken.

2. Voeg die rye bymekaar om die matriks te vereenvoudig. As jy die waardes van een ry neem en dit by `n ander ry voeg, sal die determinant van die matriks nie verander nie. Dieselfde geld vir kolomme. Jy kan dit herhaaldelik doen - of die waardes vermenigvuldig met `n konstante voordat jy optel - om soveel nulle as moontlik in die matriks te kry. Dit kan jou baie werk bespaar.

 Probeer om dieselfde truuk vir die kolomme te gebruik, om12 om `n 0 te maak.
Probeer om dieselfde truuk vir die kolomme te gebruik, om12 om `n 0 te maak.
3. Leer die truuk om driehoekmatrikse op te los. In hierdie spesiale gevalle is die determinant bloot die produk van die elemente langs die hoofdiagonaal, vanaf a11 links bo na `n33 onder regs. Ons praat steeds van 3x3-matrikse, maar `driehoekige` matrikse het spesiale waardepatrone wat nie nul nie is:
Wenke
- Hierdie metode kan gebruik word vir vierkante matrikse van enige grootte. Byvoorbeeld, as jy dit gebruik vir `n 4x4 matriks, dan hou jy na die "krap uit" `n 3x3-matriks, waarvoor jy die determinant kan bereken soos hierbo aangedui. Wees gewaarsku, want om dit met die hand te doen, sal baie vervelig wees!
- As alle elemente van `n ry of kolom gelyk is aan 0, dan is die determinant van daardie matriks gelyk aan 0.
Artikels oor die onderwerp "Bepaling van die determinant van 'n 3x3 matriks"
Оцените, пожалуйста статью
Soortgelyk
Gewilde