As jy die oppervlakte van `n vierkant wil bereken, kan jy jouself tyd bespaar deur `n sakrekenaar te gebruik en `n sy kwadraat. As een kant dus vier meter is, klik 4 en dan die vierkantige knoppie op jou sakrekenaar om die antwoord te kry. Kwadratering vermenigvuldig `n getal met homself. 
Dit word ook na verwys as cm-kwadraat, of geskryf met `n klein `2` regs bo in die eenheid, in plaas van die woord `vierkant`. 


























Bepaling van die area van 'n vorm
Inhoud
Daar is baie verskillende vorms en soveel redes waarom jy hul oppervlakte wil ken! Of jy jou huiswerk doen of probeer uitvind hoeveel verf jy nodig het om jou sitkamer oor te verf, wikiHow kan help! Begin net met Stap 1 hieronder om te leer hoe om die oppervlakte van `n vorm te bereken.
Trappe
Metode 1 van 7: Vierkante, Reghoeke en Parallelogramme

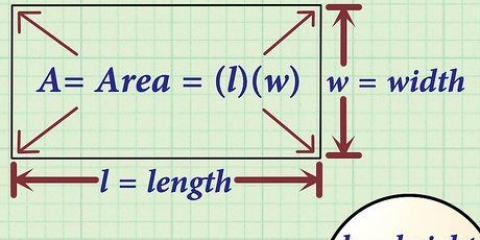
1. Meet die breedte en hoogte. Begin deur die breedte en hoogte van die vorm te bepaal (met ander woorde, deur die lengte van twee aangrensende sye te bepaal).
- Vir `n parallelogram benodig jy die basis en vertikale hoogte, maar hulle is dieselfde as die breedte en hoogte.
- In die regte wêreld moet jy dit self meet, maar vir jou huiswerk sal hierdie mates saam met die vorm gegee word.

2. Vermenigvuldig die kante. Vermenigvuldig die kante saam. Byvoorbeeld, as jy `n reghoek het met `n hoogte van 16 cm en `n breedte van 42 cm, vermenigvuldig 16 x 42.

3. Bepaal die resultaat. Die gevolglike getal uit die vermenigvuldiging is die oppervlakte van jou vorm, geskryf as `vierkante eenhede`. Die oppervlakte van ons reghoek is dus 672 vierkante cm.
Metode 2 van 7: Trapesium

1. Neem jou mates. Jy benodig die mates vanaf die basis, die bokant en die vertikale hoogte. Die basis en bokant is parallel, terwyl die hoogte langs een van die sye met die hoek gemeet word.
- In die regte wêreld moet jy dit self meet, maar vir jou huiswerk sal hierdie mates saam met die vorm gegee word.

2. Voeg die lengte van die hoogte en basis saam. Gestel die hoogte is 5 cm en die basis is 7 cm. Dit gee ons `n waarde van 12.

3. Vermenigvuldig daardie waarde met 1/2. dit gee ons `n waarde van 6.

4. Vermenigvuldig daardie waarde met die hoogte. Gestel ons het `n trapezium van 6 cm. Dit gee ons `n waarde van 36.

5. Bepaal die resultaat. Die gevolglike getal na vermenigvuldiging met hoogte is die oppervlakte van die trapezium. So met `n trapezium van 5 x 6 x 7, is die area 36 cm.
Metode 3 van 7: Omkring

1. Bepaal die radius. Om die oppervlakte van `n sirkel te vind, moet jy die radius daarvan ken. Dit is die afstand vanaf die middel van die sirkel na die rand. Jy kan dit ook bepaal met die deursnee, of die breedte van die sirkel, waarna jy dit deur twee deel.
- In die regte wêreld moet jy dit self meet, maar vir jou huiswerk sal hierdie mates saam met die vorm gegee word.

2. Vierkant die radius. Vermenigvuldig die radius met homself. Gestel ons het `n radius van 8 meter, dit gee ons `n waarde van 64.

3. Vermenigvuldig met pi. Pi (π) is `n getal met baie desimale plekke, en word in baie berekeninge gebruik. As jy `n sakrekenaar gebruik, gebruik die pi-funksie vir `n baie akkurate resultaat. Indien nie, kan jy pi afrond (die meeste van die desimale ignoreer) tot 3,14159. Dit gee ons `n produk nadat ons 201,06176 vermenigvuldig het.

4. Bepaal die resultaat. Die gevolglike getal (201.06176 in hierdie geval), is die oppervlakte van die sirkel. Ons kry dus `n resultaat van 201,06176 m.
Metode 4 van 7: Segmente

1. Bepaal die afmetings. Segmente is dele van `n sirkel wat soos waaiers lyk. Jy meet die radius van die oorspronklike sirkel, of een kant van jou `waaier`, sowel as die hoek van die punt. Gestel jy het `n radius van 14 cm en `n hoek van 60.
- In die regte wêreld moet jy dit self meet, maar vir jou huiswerk sal hierdie mates saam met die vorm gegee word.

2. Vierkant die radius. Vermenigvuldig die radius met homself. Dit gee ons `n waarde van 196 (14x14).

3. Vermenigvuldig met pi. Pi (π) is `n getal met baie desimale plekke, en word in baie berekeninge gebruik. As jy `n sakrekenaar gebruik, gebruik die pi-funksie vir `n baie akkurate resultaat. Indien nie, kan jy die pi afrond (die meeste van die desimale ignoreer) en net vermenigvuldig met 3,14159. Dit gee ons `n waarde van 615.75164.

4. Deel die hoek deur 360. Dan neem jy die hoek van die punt en deel daardie getal deur 360 (die aantal grade in `n sirkel). In hierdie geval kry ons `n waarde van ongeveer 0,166. Dit is tegnies `n herhalende nommer, maar ons gaan dit afrond om die wiskunde `n bietjie makliker te maak.

5. Vermenigvuldig die gevolglike getal met die getal wat jy vroeër bereken het. Vermenigvuldig die getal wat jy kry as jy deur 360 deel deur die getal wat jy vroeër bereken het nadat jy met pi vermenigvuldig het. In hierdie geval is die resultaat ongeveer 102 214.

6. Bereken die resultaat. Die finale getal is die oppervlakte van jou segment, wat segmente van 102,214 cm gee.
Metode 5 van 7: Ellipse

1. Bepaal die afmetings. Om die area van `n ellips te vind, moet jy die twee `strale` ken, waaraan jy kan dink as die breedte en hoogte, elk gedeel deur. Dit is die afmetings van die middel na die middel van die lang kant, en van die middel na die middel van die kortste kant. Die meetlyne sny reghoekig.
- In die regte wêreld moet jy dit self meet, maar vir jou huiswerk sal hierdie mates saam met die vorm gegee word.

2. Vermenigvuldig die twee strale. Gestel die ellips is 6 cm breed en 4 cm hoog. Dit gee ons radiusse van 3 cm en 2 cm. Nou vermenigvuldig ons hierdie getalle saam, en ons kry die produk 6 (3x2).

3. Vermenigvuldig hierdie getal met pi. Pi (π) is `n besonder lang getal en word in baie berekeninge gebruik. As jy `n sakrekenaar gebruik, gebruik die pi-funksie vir `n baie akkurate resultaat. Indien nie, kan jy die pi afrond (die meeste van die desimale ignoreer) en net vermenigvuldig met 3,14159. Dit gee ons `n waarde van 18,84954.

4. Bepaal die resultaat. Die gevolglike getal is die oppervlakte van jou ellips. In hierdie geval beteken dit dat ons ellips 18,84954 cm is.
Metode 6 van 7: Driehoek

1. Bepaal jou afmetings. Jy moet die afmetings van die basis van die driehoek ken, sowel as die hoogte. Die basis kan enige sy van die driehoek wees, solank jy die hoogte kan meet. Gestel ons het `n driehoek met `n basis van 3 meter en `n hoogte van 1 meter.
- In die regte wêreld moet jy dit self meet, maar vir jou huiswerk sal hierdie mates saam met die vorm gegee word.

2. Vermenigvuldig die basis met die hoogte. In hierdie geval kry ons `n waarde van 3 (3x1).

3. Vermenigvuldig daardie waarde met 1/2. Dit gee ons `n waarde van 1,5.

4. Bepaal die resultaat. Die gevolglike waarde is die oppervlakte van die driehoek. Ons kry dus `n resultaat van 1,5 m.
Metode 7 van 7: Komplekse vorms

1. Breek die vorm in afdelings. Jy begin deur die area vir komplekse vorms te bepaal deur die vorm in geometriese vorms op te breek, soos hierbo getoon. In huiswerkopdragte sal dit duidelik wees watter vorms hulle sal wees, maar in die regte wêreld sal jy `n vliegtuig in baie verskillende vorms moet verdeel om `n akkurate resultaat te kry.
- ’n Goeie plek om te begin is om reghoeke en ewewydige lyne te soek. Dit vorm die basis van baie vorms.

2. Bereken die oppervlakte van die individuele vorms. Gebruik die instruksies hierbo om die oppervlakte van die verskillende vorms te bepaal.

3. Voeg die vorms bymekaar. Voeg die resulterende areas bymekaar om die totale oppervlakte van jou vorm te vind.

4. Gebruik alternatiewe metodes. Daar is ander truuks wat jy ook kan probeer, afhangende van die vorm. Jy kan ook opsioneel `n denkbeeldige spasie byvoeg om die vorm `n standaard geometriese vorm te maak, en trek dan die oppervlakte van daardie denkbeeldige spasie af nadat jy die resultaat bepaal het.
Wenke
- Gebruik hierdie sakrekenaar as jy meer hulp nodig het en wil weet hoe die wiskunde werk.
- As jy dit moeilik vind, vra iemand vir hulp!
Waarskuwings
- Hou die eenhede van jou lesings dieselfde. Getalle is nie bedoel om deurmekaar te raak nie!
- Dit is altyd `n goeie idee om jou antwoord dubbel te kontroleer!
Artikels oor die onderwerp "Bepaling van die area van 'n vorm"
Оцените, пожалуйста статью
Soortgelyk
Gewilde