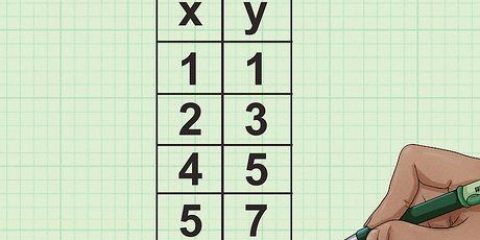
Byvoorbeeld: jy het `n driehoek met `n basis van 15 sentimeter, en `n ooreenstemmende driehoek met `n basis wat 10 cm lank is. 
Byvoorbeeld, as jy `n driehoek met basis 15 cm verminder na `n driehoek met basis 10 cm, is die verhouding  .
.
Deur die korrekte waardes in te voer, word dit .
. 
Byvoorbeeld: die verhouding  vereenvoudig kan word om
vereenvoudig kan word om . Die skaalfaktor van twee driehoeke, een met `n basis van 15 cm en een met `n basis van 10 cm, is dus
. Die skaalfaktor van twee driehoeke, een met `n basis van 15 cm en een met `n basis van 10 cm, is dus  .
. 

Byvoorbeeld, met `n skaalfaktor van 2 vergroot jy die figuur. 
Byvoorbeeld, as die skuinssy van `n reghoekige driehoek 5 sentimeter lank is, en die skaalfaktor is 2, dan bereken jy om die skuinssy van die ooreenstemmende driehoek te bepaal  . Die afgeskaalde driehoek het dus `n skuinssy van 10 cm.
. Die afgeskaalde driehoek het dus `n skuinssy van 10 cm. 
Byvoorbeeld, as die basis van `n reghoekige driehoek 3 cm is, met `n skaalfaktor van 2, bereken jy  vir die basis van die afgeskaalde driehoek. As die hoogte van `n reghoekige driehoek 4 cm lank is, met `n skaalfaktor van 2, dan bereken jy
vir die basis van die afgeskaalde driehoek. As die hoogte van `n reghoekige driehoek 4 cm lank is, met `n skaalfaktor van 2, dan bereken jy  vir die hoogte van die afgeskaalde driehoek.
vir die hoogte van die afgeskaalde driehoek. 

Onreëlmatige figure kan geskaal word as hulle sye almal eweredig is. So jy kan `n skaalfaktor bereken deur enige gegewe grootte te gebruik. Aangesien jy die breedte van enige veelhoek ken, kan jy `n verhoudingsvergelyking maak. Verhoog jy gebruik die verhouding  . As jy gaan verminder, gebruik jy die verhouding
. As jy gaan verminder, gebruik jy die verhouding  .
. Vereenvoudig die verhouding. Die verhouding  vereenvoudig kan word om
vereenvoudig kan word om  . Die verhouding
. Die verhouding  vereenvoudig kan word om
vereenvoudig kan word om  . Die twee onreëlmatige veelhoeke het dus `n skaalfaktor van
. Die twee onreëlmatige veelhoeke het dus `n skaalfaktor van  of
of  .
. 
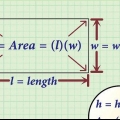
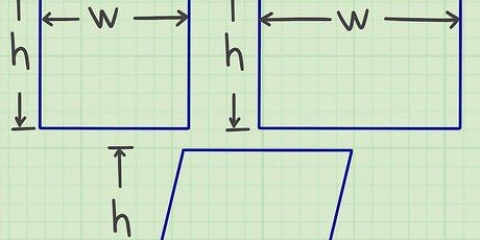
Vermenigvuldig die hoogte van die reghoek ABCD met die skaalfaktor. Dit sal jou die hoogte van die reghoek EFGH gee:  .
. Vermenigvuldig die breedte van reghoek ABCD met die skaalfaktor. Dit sal jou die breedte van reghoek EFGH gee:  .
. Vermenigvuldig die hoogte en breedte van reghoek EFGH vir die area:  . Dus, die oppervlakte van die reghoek EFGH is 150 cm2.
. Dus, die oppervlakte van die reghoek EFGH is 150 cm2. 

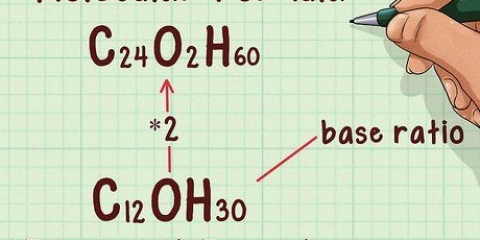
Byvoorbeeld: om die molekulêre formule van die betrokke stof te bepaal, vermenigvuldig die subskripsie van H2O met die skaalfaktor 3. H2O * 3 = H6O3 
Byvoorbeeld: die skaalfaktor vir die verbinding is 3. Die molekulêre formule van die stof is H6O3.
Bepaling van die skaalfaktor
Inhoud
Die (lineêre) skaalfaktor is die verhouding van twee ooreenstemmende sye van figure van dieselfde vorm. Soortgelyke figure het dieselfde vorm maar verskillende groottes. Die skaalfaktor word gebruik om eenvoudige meetkundige probleme op te los. Jy kan die skaalfaktor gebruik om die onbekende sye van `n figuur te bepaal. Omgekeerd kan jy die lengte van die sy van twee soortgelyke getalle gebruik om die skaalfaktor te bereken. Sulke probleme vereis dat jy breuke vermenigvuldig of vereenvoudig.
Trappe
Metode 1 van 4: Bepaling van die skaalfaktor van `n geskaalde figuur

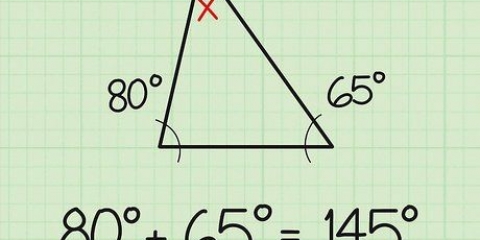
1. Kyk of die syfers soortgelyk is. Figure van dieselfde vorm het dieselfde hoeke en die lengtes van die sye is eweredig. Soortgelyke figure het dieselfde vorm, maar een figuur is groter as die ander.
- Die stelling moet aandui dat die vorms gelyk is, of wys dat die hoeke dieselfde is, anders dui aan dat die lengteverhouding van die sye eweredig aan skaal is, of dat hulle met mekaar ooreenstem.

2. Vind `n bypassende sy van elke figuur. Jy sal dalk die figuur moet draai of omdraai sodat die twee vorms in lyn is en jy die ooreenstemmende sye herken. Die lengte van hierdie twee sye moet gegee word, of jy moet hulle kan meet. As geen sylengte van elke figuur bekend is nie, kan jy nie die skaalfaktor vind nie.

3. Stel die verhouding vas. Vir elke paar bypassende figure is daar twee skaalfaktore: een wat jy gebruik wanneer jy `n figuur vergroot en een wat jy gebruik wanneer jy krimp. As jy vergroot na `n groter weergawe, gebruik die verhouding  . Gebruik die verhouding wanneer jy die grootte van `n figuur verander
. Gebruik die verhouding wanneer jy die grootte van `n figuur verander  .
.
 . Gebruik die verhouding wanneer jy die grootte van `n figuur verander
. Gebruik die verhouding wanneer jy die grootte van `n figuur verander  .
. .
.Deur die korrekte waardes in te voer, word dit
 .
.
4. Vereenvoudig die verhouding. Die vereenvoudigde verhouding, of breuk, gee jou die skaalfaktor. As jy verminder sal die skaalfaktor `n gereelde breuk wees. As jy vergroot, word dit `n heelgetal of `n onbehoorlike breuk, wat jy na `n desimale kan omskakel.
 vereenvoudig kan word om
vereenvoudig kan word om . Die skaalfaktor van twee driehoeke, een met `n basis van 15 cm en een met `n basis van 10 cm, is dus
. Die skaalfaktor van twee driehoeke, een met `n basis van 15 cm en een met `n basis van 10 cm, is dus  .
.Metode 2 van 4: Bepaal `n ooreenstemmende syfer deur die skaalfaktor te gebruik

1. Bepaal die lengte van die sy van die figuur. Jy benodig een figuur waarvan die sye gegee of meetbaar is. As jy nie die sylengte van die prent kan bepaal nie, kan jy nie `n afgeskaalde figuur skep nie.
- Byvoorbeeld: jy het `n reghoekige driehoek met sye van 4 cm en 3 cm en `n skuinssy van 5 cm.

2. Besluit of om te vergroot of te verklein. As jy vergroot, sal jou ontbrekende syfer groter word en die skaalfaktor sal `n heelgetal, onbehoorlike breuk of desimale wees. Soos jy krimp, word die syfer kleiner, en jou skaalfaktor is heel waarskynlik `n gereelde breuk.

3. Vermenigvuldig die lengte van `n sy met die skaalfaktor. Die skaalfaktor moet gegee word. Deur die lengte van die sy met die skaalfaktor te vermenigvuldig gee die ontbrekende kant van die skaalfiguur terug.
 . Die afgeskaalde driehoek het dus `n skuinssy van 10 cm.
. Die afgeskaalde driehoek het dus `n skuinssy van 10 cm.
4. Bepaal die ander kante van die figuur. Gaan voort om elke kant met die skaalfaktor te vermenigvuldig. Dit sal jou die ooreenstemmende kante van die ontbrekende figuur gee.
 vir die basis van die afgeskaalde driehoek. As die hoogte van `n reghoekige driehoek 4 cm lank is, met `n skaalfaktor van 2, dan bereken jy
vir die basis van die afgeskaalde driehoek. As die hoogte van `n reghoekige driehoek 4 cm lank is, met `n skaalfaktor van 2, dan bereken jy  vir die hoogte van die afgeskaalde driehoek.
vir die hoogte van die afgeskaalde driehoek.Metode 3 van 4: Enkele voorbeeldoefeninge

1. Bepaal die skaalfaktor van hierdie ooreenstemmende figure: `n reghoek met `n hoogte van 6 cm, en `n reghoek met `n hoogte van 54 cm.
- Vergelyk die twee hoogtes. Om te verhoog, is die verhouding
. Om te krimp, gebruik die verhouding
.
- Vereenvoudig die verhouding. Die verhouding
vereenvoudig kan word om
. Die verhouding
vereenvoudig kan word om
. Die twee reghoeke het dus `n skaalfaktor van
of
.

2. Probeer die volgende taak. ’n Onreëlmatige veelhoek is 14 cm lank op sy breedste punt. `n Ooreenstemmende onreëlmatige veelhoek is 8 cm op die breedste deel. Wat is die skaalfaktor?
 . As jy gaan verminder, gebruik jy die verhouding
. As jy gaan verminder, gebruik jy die verhouding  .
. vereenvoudig kan word om
vereenvoudig kan word om  . Die verhouding
. Die verhouding  vereenvoudig kan word om
vereenvoudig kan word om  . Die twee onreëlmatige veelhoeke het dus `n skaalfaktor van
. Die twee onreëlmatige veelhoeke het dus `n skaalfaktor van  of
of  .
.
3. Gebruik die skaalfaktor om die volgende probleem te beantwoord. Reghoek ABCD is 8 cm x 3 cm. reghoek EFGH is `n groter, ooreenstemmende reghoek. Gegee is `n skaalfaktor van 2,5. Wat is die oppervlakte van reghoek EFGH?
 .
. .
. . Dus, die oppervlakte van die reghoek EFGH is 150 cm2.
. Dus, die oppervlakte van die reghoek EFGH is 150 cm2.Metode 4 van 4: Die skaalfaktor in chemie

1. Verdeel die molêre massa van `n stof deur dié van die empiriese formule. Wanneer jy die empiriese formule van `n chemiese verbinding ken en jy benodig die molekulêre formule van dieselfde chemiese stof, kan jy die skaalfaktor vind wat jy nodig het deur die molêre massa van die stof deur die molêre massa van die empiriese formule te deel.
- Byvoorbeeld: jy wil die molêre massa van `n H2O-verbinding met `n molêre massa van 54.05 g/mol weet.
- Die molêre massa van H2O is 18,0152 g/mol.
- Bepaal die skaalfaktor deur die molêre massa van die verbinding deur die molêre massa van die empiriese formule te deel:
- Skaalfaktor = 54,05 / 18,0152 = 3

2. Vermenigvuldig die empiriese formule met die skaalfaktor. Vermenigvuldig die subskripsie van elke element binne die empiriese formule met die skaalfaktor wat jy pas bereken het. Dit sal jou die molekulêre formule van die verbinding gee.

3. Skryf die antwoord neer. Met hierdie antwoord het jy die korrekte antwoord vir die empiriese formule sowel as die molekulêre formule van die chemiese binding gevind.
Artikels oor die onderwerp "Bepaling van die skaalfaktor"
Оцените, пожалуйста статью
Soortgelyk
Gewilde