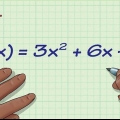Bepaling van 'n afgeleide

1. Verstaan ​​die notasie van `n afgeleide. Die volgende twee maniere van notasie is die algemeenste, maar talle ander maniere kan gevind word op Wikipedia.

• Leibniz Notasie Hierdie notasie word die meeste gebruik wanneer die vergelyking ay en x bevat. Dy/dx beteken letterlik "die afgeleide van y met betrekking tot x". Probeer om daaraan te dink as Δy/Δx vir die waardes van x en y waar die verskil oneindig klein is. Hierdie verduideliking gee natuurlik die definisie van `n limiet met betrekking tot die afgeleide: lim<sub>h->0</sub> (f(x+h)-f(x))/h. Deur hierdie notasie op die tweede afgeleide toe te pas, skryf: dy/dx.
• Lagrange se Notasie Die afgeleide van `n funksie f word ook geskryf as f`(x). Hierdie notasie word uitgespreek as "die funksie f van x". Hierdie notasie is korter as Leibniz s`n en word gebruik wanneer `n afgeleide as `n funksie beskou word. Vir hoër afgeleides voeg net nog een by " ` " reg vir "f", laat die tweede afgeleide soos f``(x) lyk.

2. Verstaan ​​wat `n afgeleide is en waarvoor dit gebruik word. Eerstens, om die helling van `n lineêre grafiek te vind, word twee punte op die lyn geneem en hierdie koördinate word in die vergelyking ingevoeg (y₂ - y₁)/(X₂ - X₁). Maar dit is slegs moontlik met lineêre grafieke. Vir kwadratiese vergelykings en hoër is die grafiek `n kromme, dus is die verskil tussen twee punte nie akkuraat genoeg nie. Om die helling van `n raaklyn van `n parabool te vind, word twee punte geneem en in die vergelyking gevul om die helling van `n geboë lyn te bepaal: [f(x + dx) - f(x)]/dx. Dx beteken"delta x," wat is die verskil tussen die twee x-koördinate van die twee punte van die grafiek. Let daarop dat hierdie vergelyking dieselfde is as (y₂ - y₁)/(X₂ - X₁), maar in `n ander vorm. Aangesien dit reeds bekend is dat die resultaat nie akkuraat sal wees nie, word `n indirekte benadering gekies. Om die helling van die raaklyn by die punt (x, f(x)) te vind, moet dx 0 nader sodat die twee gekose punte amper dieselfde is.Maar jy kan nie deur 0 deel nie, so nadat jy die waardes van die twee punte ingevul het, moet jy dedx in die noemer uitskakel. As dit suksesvol is, maak dx gelyk aan 0 en los op. Dit is die helling van die raaklyn by (x, f(x)). Die afgeleide van `n vergelyking is die algemene vergelyking om die helling van enige raaklyn van `n grafiek te vind. Dit lyk dalk baie moeilik, maar die voorbeelde hieronder sal jou wys hoe om die afgeleide te bepaal.

1. Gebruik eksplisiete differensiasie as y reeds aan die een kant van die vergelyking is.

2. Vervang een vergelyking in `n ander vergelyking [f(x + dx) - f(x)]/dx. Byvoorbeeld, die vergelyking y = x, waarvan die afgeleide [(x + dx) - x]/dx is.

3. Brei dx verder uit om die vergelyking [dx(2x + dx)]/dx te kry. Nou is dit moontlik om die dx in die teller en noemer uit te skakel. Die resultaat is 2x + dx, en soos dx 0 nader, word die afgeleide 2x. Dit is die helling van enige raaklyn aan die grafiek y = x is 2x. Tik net die waarde van `n gegewe punt x waarvan jy die raaklyn wil vind in die vergelyking in.

4. Leer om die patrone van dieselfde soort vergelykings te herken. Hieronder vind u `n paar.

1. Gebruik implisiete differensiasie wanneer jou vergelyking nie bloot geskryf kan word met die y aan die een kant van die gelykheidsteken. Selfs as jy dit met die y aan die een kant skryf, sal die berekening van dy/dx steeds `n taak wees. Hieronder is `n voorbeeld van hoe om hierdie tipe vergelyking op te los.

2. In hierdie voorbeeld, xy + 2y = 3x + 2y, vervang jey met f(x), sodat dit duidelik is dat dit eintlik `n funksie is. Die vergelyking word dan xf(x) + 2[f(x)] = 3x + 2f(x).

3. Om die afgeleide van hierdie vergelyking te vind, onderskei (`n indrukwekkende woord om die afgeleide te vind) jou beide kante van die vergelyking met betrekking tot x. Die vergelyking word dan xf`(x) + 2xf(x) + 6[f(x)]f`(x) = 3 + 2f`(x).

4. Vervang f(x) weer met y. Wees versigtig om dit nie met f`(x) te doen nie, aangesien dit baie verskil van f(x).

5. Los op vir f`(x). Die antwoord van hierdie voorbeeld is (3 - 2xy)/(x + 6y - 2).

1. Om die hoër afgeleide van `n funksie te neem, beteken net om die afgeleide van die afgeleide te neem. Byvoorbeeld, as die derde afgeleide gevra word, neem jy die afgeleide van die afgeleide van die afgeleide. Vir sommige vergelykings word `n hoër afgeleide gelyk aan 0.

1. As y `n differensieerbare funksie van z is, en z `n differensieerbare funksie van x is, dan is y `n saamgestelde funksie van x, en die afgeleide van y met betrekking tot x (dy/dx) is (dy/du)*(du) /dx). Die kettingreël kan ook `n saamgestelde vergelyking wees, soos volg: (2x - x). Om die afgeleide hiervan te vind; Dink net soos jy met die produkreeks doen. Vermenigvuldig die vergelyking met die eksponent en verminder die eksponent met 1. Vermenigvuldig dan die vergelyking met die afgeleide wat onder die eksponent val (in hierdie geval, 2x^4 - x). Die antwoord op hierdie probleem word dan 3(2x - x)(8x - 1).