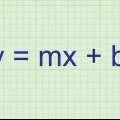Verwerk dan -1 in die funksie om die y-koördinaat te kry. f(-1) = 3(-1) + 6(-1) -2 = 3 - 6 -2 = -5. Die hoekpunt van die parabool is (-1,-5). Verwerk dit in die grafiek deur `n punt by x-koördinaat -1 en y-koördinaat -5 te teken. Dit moet in die derde kwadrant van die grafiek wees. 
f(-2) = 3(-2) + 6(-2) -2 = -2. `n Punt op die grafiek is (-2, -2) f(0) = 3(0) + 6(0) -2 = -2. Nog `n punt op die grafiek is (0,-2) f(1) = 3(1) + 6(1) -2 = 7. `n Derde punt op die grafiek is (1, 7). 



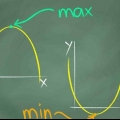
Maar veronderstel y = -3 is die laagste punt van die grafiek, maar styg vir ewig. Dan is die reeks f(x) ≥ -3, en nie meer as dit nie. Gestel die grafiek bereik sy hoogste punt by y=10, maar hou dan aan om vir ewig te daal. Dan is die reeks f(x) ≤ 10. 






Byvoorbeeld: As sy 2 kaartjies verkoop sal jy 2 met 5 moet vermenigvuldig, met 10 as die antwoord, en dus die totale bedrag wat ingesamel is. 

Dit wil sê, enige positiewe heelgetal wat `n veelvoud van vyf is, is `n moontlike uitkoms van die funksie.
Bepaling van die omvang van 'n funksie
Inhoud
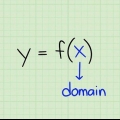
Die omvang van `n funksie is die stel getalle wat die funksie kan produseer. Met ander woorde, dit is die stel y-waardes wat jy kry wanneer jy alle moontlike x-waardes in die funksie inreken. Hierdie stel x-waardes word die domein genoem. As jy wil weet hoe om die omvang van `n funksie te bereken, volg die stappe hieronder.
Trappe
Metode 1 van 4: Bepaal die omvang van `n funksie met `n gegewe vergelyking

1. Skryf die vergelyking neer. Gestel jy het die volgende vergelyking: f(x) = 3x + 6x -2. Dit beteken dat wanneer jy `n waarde vir die invoer X van die vergelyking, dat jy dan `n het y-waarde kry. Dit is die funksie van `n parabool.

2. Vind die hoekpunt van die funksie as dit `n kwadratiese vergelyking is. As jy `n reguit lyn of enige funksie met `n polinoom of `n onewe getal het, soos f(x) = 6x+2x + 7, kan jy hierdie stap oorslaan. Maar as jy met `n parabool of `n vergelyking te doen het waar die x-koördinaat kwadraat of verhoog word met `n ewe mag, sal jy die hoekpunt van die parabool moet teken. Om dit te doen, gebruik die vergelyking -b/2a vir die x-koördinaat van die funksie 3x + 6x -2, waar 3 = a, 6 = b en -2 = c. In hierdie geval, -b is -6 en 2a is 6, dus is die x-koördinaat -6/6, of -1.

3. Soek `n paar ander punte van die funksie. Om `n gevoel vir die funksie te kry, moet jy `n paar ander waardes vir x invul sodat jy `n idee kan kry van hoe die funksie lyk voordat jy na die reeks begin soek. Aangesien dit `n parabool is en x positief is, sal die parabool na bo wys (vallei-parabool). Maar net om seker te maak, voer ons nog `n paar waardes vir x in om te sien watter y-koördinate hulle oplewer:

4. Vind die omvang van die grafiek. Kyk nou na die y-koördinate op die grafiek en vind die laagste punt waar die grafiek aan die y-koördinaat raak. In hierdie geval is die laagste y-koördinaat aan die bokant van die parabool, -5 en die grafiek strek oneindig verder as hierdie punt. Dit beteken dat die omvang van die funksie y = alle reële getalle ≥ -5.
Metode 2 van 4: Bepaal die omvang van `n funksie deur `n grafiek te gebruik

1. Vind die minimum van die funksie. Vind die laagste y-koördinaat van die funksie. Gestel die funksie bereik sy laagste punt by -3. Hierdie funksie kan kleiner en kleiner word, tot oneindig, so dit het geen vaste laagste punt nie - net oneindig.

2. Vind die maksimum van die funksie. Gestel die hoogste y-koördinaat van die funksie is 10. Hierdie funksie kan ook oneindig groter word, dus het dit geen vaste hoogste punt nie – net oneindig.

3. Dui aan wat die reeks is. Dit beteken dat die omvang van die funksie, of die omvang van die y-koördinate, van -3 tot 10 is. Dus, -3 ≤ f(x) ≤ 10. Dit is die omvang van die funksie.
Metode 3 van 4: Bepaling van die omvang van `n verhouding se funksie

1. Skryf die verhouding neer. `n Verwantskap is `n stel geordende pare x- en y-koördinate. Jy kan na `n verhouding kyk en die domein en omvang daarvan bepaal. Gestel jy het met die volgende verband te doen: {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}.

2. Lys die y-koördinate van die verhouding. Om die omvang van die verwantskap te bepaal, skryf ons alle y-koördinate van elke geordende paar neer: {-3, 6, -1, 6, 3}.

3. Verwyder alle duplikaatkoördinate sodat jy net een van elke y-koördinaat het. Jy het dalk opgemerk dat jy die "6" twee keer in die lys. Verwyder dit sodat jy oorbly met {-3, -1, 6, 3}.

4. Skryf die omvang van die verwantskap in stygende volgorde. Rangskik dan die getalle in die stel van die kleinste na die grootste, en jy het die reeks gevind. Die omvang van die verband {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} is {-3,-1, 3, 6}. Jy is gereed.

5. Maak die verhouding `n funksie is. Vir `n verband om `n funksie te wees, elke keer as jy `n getal vanaf `n x-koördinaat invoer, moet die y-koördinaat dieselfde wees. Byvoorbeeld, die verhouding {(2, 3) (2, 4) (6, 9)} is geen funksie, want as jy vir die eerste keer die 2 as x invul, kry jy `n 3 as waarde, maar die tweede keer wat jy `n 2 invul, kry jy vier. `n Verhouding is slegs `n funksie as jy altyd dieselfde uitset kry vir `n sekere inset. As jy -7 invoer, behoort jy altyd dieselfde y-koördinaat te kry (wat dit ook al mag wees), elke keer.
Metode 4 van 4: Bepaal die omvang van `n funksie in `n probleem

1. Lees die uitgawe. Gestel jy werk aan die volgende probleem: "Becky verkoop kaartjies vir haar skool se talentprogram vir $5 elk. Die totale bedrag wat sy insamel is `n funksie van die aantal kaartjies wat sy verkoop. Wat is die omvang van die funksie?"

2. Skryf die probleem as `n funksie. In hierdie geval m die bedrag wat ingesamel is en t die aantal kaartjies verkoop. Aangesien elke kaartjie 5 euro kos, sal jy die aantal kaartjies wat verkoop is met 5 moet vermenigvuldig om die totale bedrag te kry. Daarom kan die funksie geskryf word as M(t) = 5t.

3. Bepaal wat die domein is. Om die reeks te vind, benodig jy eers die domein. Die domein bestaan uit alle moontlike waardes van t wat aan die vergelyking deelneem. In hierdie geval kan Becky 0 of meer kaartjies verkoop – sy kan nie `n negatiewe aantal kaartjies verkoop nie. Aangesien ons nie die aantal sitplekke in die skool se ouditorium weet nie, kan ons aanvaar dat sy in teorie `n oneindige aantal kaartjies kan verkoop. En sy kan net hele kaartjies verkoop, nie `n deel daarvan nie. Daarom is die domein van die funksie t = enige positiewe heelgetal.

4. Bepaal wat die reeks is. Die reeks is die moontlike bedrag wat Becky met die verkoop kan insamel. Jy sal met die domein moet werk om die reeks te vind. As jy weet dat die domein bestaan uit `n positiewe heelgetal en dat die vergelyking M(t) = 5t dan weet jy ook dat jy enige positiewe heelgetal in hierdie funksie kan invoer vir die antwoord, of reeks. Byvoorbeeld: As sy 5 kaartjies verkoop, dan is M(5) = 5 x 5, of 25 euro. As sy 100 verkoop, dan is M(100) = 5 x 100, of 500 euro. Daarom is die omvang van die funksie enige positiewe heelgetal wat `n veelvoud van vyf is.
Wenke
- Kyk of jy die inverse van die funksie kan vind. Die domein van die inverse van `n funksie is gelyk aan die omvang van daardie funksie.
- In die moeiliker gevalle kan dit makliker wees om eers die grafiek met behulp van die domein te teken (indien nodig) en dan die reeks vanaf die grafiek te lees.
- Kyk of die funksie herhaal. Enige funksie wat langs die x-as herhaal sal dieselfde reeks vir die hele funksie hê. Byvoorbeeld: f(x) = sin(x) het `n reeks tussen -1 en 1.
Artikels oor die onderwerp "Bepaling van die omvang van 'n funksie"
Оцените, пожалуйста статью
Soortgelyk
Gewilde