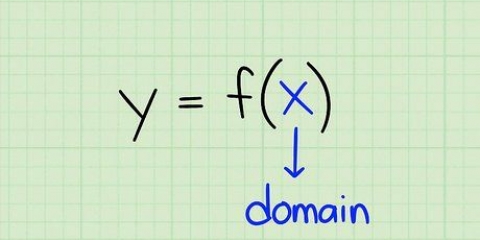
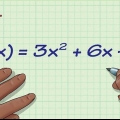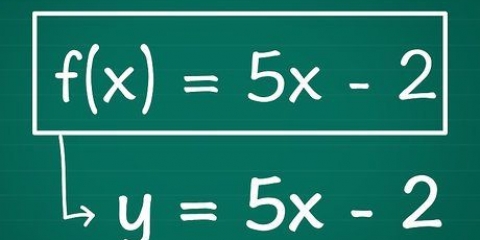Byvoorbeeld: die standaardfunksie f(x) = 2x +16x + 39. Hier het ons a = 2, b = 16 en c = 39. In hoekpuntnotasie: f(x) = 4(x - 5) + 12. Hier het ons a = 4, h = 5, en k = 12. 
Voorbeeld 1. (f(x) = 2x +16x + 39), h = -b/2a = -16/2(2). As ons dit oplos, sien ons dat h = -4. Voorbeeld 2. (f(x) = 4(x - 5) + 12), sien ons dadelik dat h = 5. 
Ons het byvoorbeeld 1 gesien dat h = -4. Om nou k te vind, los ons hierdie vergelyking op deur hierdie waarde van h in die vergelyking in te voeg, vir die veranderlike x: k = 2(-4) + 16(-4) + 39. k = 2(16) - 64 + 39. k = 32 - 64 + 39 = 7 Uit voorbeeld 2 weet ons dat die waarde van k gelyk is aan 12, sonder dat `n berekening nodig is. 
In voorbeeld 1 is die bokant van die grafiek (-4.7). Teken die punt op jou grafiek en maak seker dat jy die koördinate korrek benoem. In voorbeeld 2 is die bokant (5,12). So vanaf die punt (0,0) gaan jy 5 plekke na regs en dan 12 op. 
In die geval van voorbeeld 1 is die simmetrie-as die lyn parallel aan die y-as en gaan deur die punt (-4, 7). Alhoewel dit nie deel van die parabool self is nie, kan die lig van hierdie gids jou wys hoe simmetries die kromme van die parabool is. 
In voorbeeld 1 het ons te doen met die funksie (f(x) = 2x +16x + 39), en dit is dus `n valleiparabool, want a = 2 (positief). In voorbeeld 2 het ons te doen met die funksie f(x) = 4(x - 5) + 12), en dit is ook `n valleiparabool omdat a = 4 (positief). 
Bepaal dat f(x) = 0 en los die vergelyking op. Hierdie metode kan werk vir eenvoudige kwadratiese vergelykings, veral in die hoekpuntvorm, maar jy sal vind dit word moeiliker en moeiliker namate die funksies meer kompleks word. Hieronder is `n paar voorbeelde. f(x) = 4(x - 12) 0 = 4(x - 12) - 4 4 = 4(x - 12) 1 = (x - 12) SqRt(1) = (x - 12) +/- 1 = x -12. x = 11 en 13 is die snypunte met die x-as van die parabool. Faktoreer die vergelyking. Sommige vergelykings van die vorm ax + bx + c kan maklik herskryf word as (dx + e)(fx +g), waar dx × fx = ax, (dx × g + fx × e) = bx, en e × g = c. In hierdie geval is die x-afsnitte die waardes van x waar elke term binne die hakies 0 word. Byvoorbeeld: x + 2x + 1 = (x + 1)(x + 1) In hierdie geval is die snypunt gelyk aan -1, want wanneer dit met beide faktore ingevul word, lewer dit nul. Gebruik die abc-formule. As dit nie maklik is om die kruisings uit te vind of die vergelyking te faktoriseer nie, gebruik die "abc formule" wat spesiaal hiervoor bedoel is. Aanvaar `n vergelyking in die vorm ax + bx + c. Voer dan die waardes van a, b en c in die formule x = (-b +/- SqRt(b - 4ac))/2a in. Let daarop dat dit jou dikwels twee antwoorde vir x gee, wat goed is - dit beteken net dat jou parabool twee snypunte met die x-as het. Hier is `n voorbeeld: -Voeg 5x + 1x + 10 in die vergelyking soos volg in: x = (-1 +/- SqRt(1 - 4(-5)(10)))/2(-5) x = (-1 +/- SqRt(1 + 200))/-10 x = (-1 +/- SqRt(201))/-10 x = (-1 +/- 14,18)/-10 x = (13,18/-10) en (-15,18/-10). Die snypunte van die parabool met die x-as is ongeveer x = -1 318 en 1 518 Soos in voorbeeld 1 met die vergelyking 2x + 16x + 39, sal dit soos volg lyk: x = (-16 +/- SqRt(16 - 4(2)(39))))/2(2) x = (-16 +/- SqRt(256 - 312))/4 x = (-16 +/- SqRt(-56)/-10 Aangesien dit nie moontlik is om die vierkantswortel van `n negatiewe getal te vind nie, weet ons dat daar geen kruisings met die x-as vir hierdie spesifieke parabool bestaan nie. 
Ons weet byvoorbeeld dat ons kwadratiese vergelyking 2x + 16x + 39 `n snypunt y = 39 het, maar ons kan dit ook soos volg vind: f(x) = 2x + 16x + 39 f(x) = 2(0) + 16(0) + 39 f(x) = 39. Die snyding van die parabool met die y-as: y = 39. Soos hierbo aangedui, kan ons die kruising maklik lees omdat y = c. Die vergelyking 4(x - 5) + 12 het `n snypunt met die y-as wat soos volg gevind kan word: f(x) = 4(x - 5) + 12 f(x) = 4(0 - 5) + 12 f(x) = 4(-5) + 12 f(x) = 4(25) + 12 f(x) = 112. Die kruising met die y-as: y = 112. 
Kom ons kyk weer na die vergelyking x + 2x + 1. Ons weet reeds dat die enigste snypunt met die x-as (-1.0) is. Aangesien dit slegs raak aan die x-as op hierdie punt, kan ons aflei dat die hoekpunt van die grafiek gelyk is aan hierdie punt. Tot dusver het ons net een punt van hierdie parabool – nie naastenby genoeg om `n grafiek te kan teken nie. Kom ons soek nog `n paar punte om seker te maak ons het meer waardes. Kom ons probeer om die y-waardes te vind wat met die volgende x-waardes geassosieer word: 0, 1, -2 en -3. x=0: f(x) = (0) + 2(0) + 1 = 1. Dan is die punt (0.1). x=1: f(x) = (1) + 2(1) + 1 = 4. Dan is die punt (1,4). x=-2: f(x) = (-2) + 2(-2) + 1 = 1. Dan is die punt (-2.1). x=-3: f(x) = (-3) + 2(-3) + 1 = 4. Dan is die punt (-3.4). Plaas hierdie punte in die grafiek en teken jou parabool. Let daarop dat die parabool heeltemal simmetries is - as jy die punte aan die een kant van die grafiek ken, kan jy jouself gewoonlik baie werk bespaar deur hierdie punte te gebruik om die punte aan die ander kant van die simmetrie-as te vind.
Teken 'n funksie
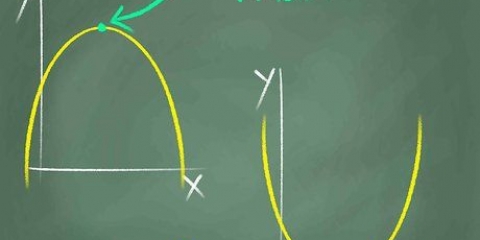
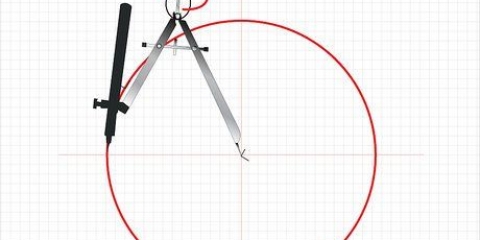
Soos `n grafiek sien `n kwadratiese vergelyking byl + bx + c, ook enige geskryf asa(x - h) + k, lyk soos `n gladde U-vormige kromme. Dit is wat ons noem a parabool. Om `n kwadratiese vergelyking te teken behels die vind van die hoekpunt, rigting en dikwels snypunte met die x-as en die y-as. In die geval van die relatief eenvoudige kwadratiese vergelyking kan dit ook voldoende wees om `n aantal waardes vir x in te voer om hierdie punte in die koördinaatstelsel aan te dui, waarna die parabool geteken kan word. Gaan voort na stap 1 om te begin.
Trappe

1. Bepaal watter soort kwadratiese vergelyking jy het. Dit kan op twee maniere geskryf word: die standaardnotasie en die hoekpuntnotasie (nog `n manier om die vierkantswortelformule te skryf). Jy kan albei gebruik om `n grafiek van `n kwadratiese vergelyking te maak, maar hierdie proses verskil in beide gevalle effens. Gewoonlik sal jy die standaardvorm teëkom, maar dit maak beslis nie seer om te leer om albei vorms te gebruik nie. Die twee vorme van `n kwadratiese vergelyking is: Die hoekpunt vorm. Hier word die kwadratiese vergelyking geskryf as: f(x) = a(x - h) + k waar a, h en k reële getalle is en a nie gelyk aan nul is nie. Hierdie vorm word hoekpunt genoem omdat h en k direk verwys na die hoekpunt van jou parabool by die punt (h,k). Twee voorbeelde van vergelykings in hoekpuntvorm is f(x) = 9(x - 4) + 18 en -3(x - 5) + 1 Om `n grafiek van hierdie vergelykings te kan maak, bepaal ons eers die bokant (h,k) van die grafiek. In die standaardvergelyking kan jy dit vind via: h = -b/2a en k = f(h), terwyl dit reeds in hoekpuntvorm gegee word omdat h en k in die vergelyking voorkom.
- Die standaard vorm. Hier word die kwadratiese vergelyking geskryf as: f(x) = ax + bx + c waar a, b en c reële getalle is en a nie gelyk aan nul is nie.
- Twee voorbeelde van standaard kwadratiese vergelykings: f(x) = x + 2x + 1 en f(x) = 9x + 10x -8.

2. Bepaal jou veranderlikes. Om `n kwadratiese vergelyking op te los is dit gewoonlik nodig om die veranderlikes a, b en c (of a, h en k) te bepaal. `n Gewone probleem sal vir jou `n kwadratiese vergelyking in die standaardvorm gee, maar die hoekpuntnotasie kan ook voorkom.

3. Bereken h. In die hoekpuntnotasie is die waarde van h reeds gegee, maar in die standaardnotasie moet hierdie waarde nog bereken word. Onthou dat vir die standaardvergelyking, h = -b/2a.

4. Bereken k. Soos met h, is k reeds bekend vir vergelykings in die hoekpuntvorm. Vir vergelykings in standaardnotasie, onthou dat k = f(h). Met ander woorde, jy kan k vind deur elke veranderlike x met die waarde van h te vervang.

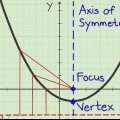
5. Teken die bo- of onderkant van die grafiek. Die kruin of vallei van jou parabool is die punt (h, k) - h verteenwoordig die x-koördinaat en k verteenwoordig die y-koördinaat. Die kruin is die middelpunt van jou parabool — die hoogste of laagste punt, die kruin of die trog, van `n grafiek in die vorm van `n "JY" of andersom. Om die hoekpunt van `n parabool te kan bepaal is `n noodsaaklike deel daarvan om `n korrekte grafiek te kan teken – dikwels is die bepaling van die hoekpunt van `n parabool deel van `n wiskundeprobleem op skool.

6. Teken die simmetrie-as van die parabool. Die simmetrie-as van `n parabool is die lyn wat die figuur in die middel sny en dit presies in die helfte verdeel. Een kant van die grafiek word langs hierdie lyn in die ander kant van die grafiek weerspieël. Vir kwadratiese vergelykings van óf die vorm ax + bx + c óf a(x - h) + k, is hierdie as die lyn parallel aan die y-as wat deur die hoekpunt van die parabool gaan.

7. Bepaal die rigting van die parabool. Nadat jy uitgevind het wat die bokant van die parabool is, is dit nodig om te weet of jy met `n bergparabool of `n valleiparabool te doen het, dit wil sê of die opening onder of bo is. Gelukkig is dit baie eenvoudig. as "a" positief jy het met `n vallei-parabool te doen; is "a" negatief dan is dit `n bergparabool (met die opening aan die onderkant)

8. Bepaal, indien nodig, die snypunte van die parabool. In wiskundeprobleme word jy dikwels gevra om die snypunte van die parabool met die x-as te gee (dit is "nul", a of twee punte waar die parabool die x-as sny of raak). Selfs as dit nie versoek word nie, is hierdie punte baie belangrik om `n akkurate grafiek te kan teken. Maar nie alle parabole sny met die x-as nie. As jy met `n valleiparabool te doen het en die valleipunt is bo die x-as of, in die geval van `n bergparabool, net onder die x-as, dan is daar eenvoudig geen kruisings te vinde nie. Indien wel, gebruik een van die volgende metodes:

9. Indien nodig, bepaal die snypunt van die parabool met die y-as. Dit is dikwels nie nodig nie, maar soms nodig om hierdie snypunt te vind, byvoorbeeld vir `n wiskundeprobleem. Dit is redelik maklik - stel die waarde van x op 0 en los die vergelyking vir f(x) of y op, wat jou die y-waarde gee van die punt waar die parabool met die y-as sny. Die verskil met die snypunte deur die x-as is dat daar met die y-as altyd net een snypunt is. Let wel – vir standaardvergelykings is die snypunt met die y-as by y = c.

10. As jy dit nodig vind, teken eers ekstra punte en dan die hele grafiek. Jy behoort nou `n piek of vallei, `n rigting, kruisings met die x-as en moontlik met die y-as van jou vergelyking te hê. Vanaf hierdie punt kan jy probeer om die parabool te teken deur hierdie punte te gebruik of jy kan probeer om meer punte te vind om die grafiek meer akkuraat te maak. Die maklikste manier om dit te doen is bloot deur `n aantal x-waardes in te vul, wat `n aantal y-waardes terugstuur. Jy sal dikwels (deur die onderwyser) gevra word om eers `n aantal punte te bereken voordat jy die parabool kan teken.
Wenke
- Rond getalle af indien nodig of gebruik breuke. Dit kan help om `n grafiek korrek te vertoon.
- Let daarop dat as, vir die funksie f(x) = ax + bx + c, b of c gelyk aan nul is, sal daardie terme verdwyn. Byvoorbeeld, 12x + 0x + 6 is gelyk aan 12x + 6 omdat 0x gelyk is aan 0.
Artikels oor die onderwerp "Teken 'n funksie"
Оцените, пожалуйста статью
Gewilde